2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.2.2对数函数及其性质课件新人教A版必修1(16张)
文档属性
| 名称 | 2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.2.2对数函数及其性质课件新人教A版必修1(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 394.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 00:00:00 | ||
图片预览




文档简介
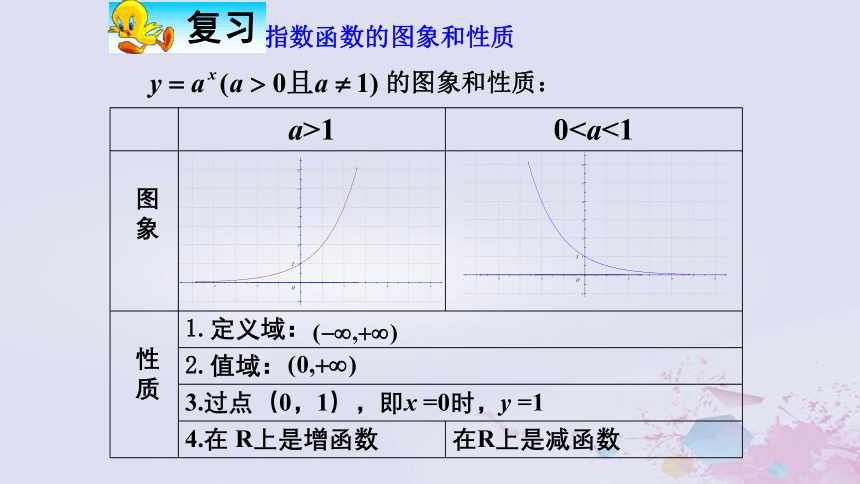
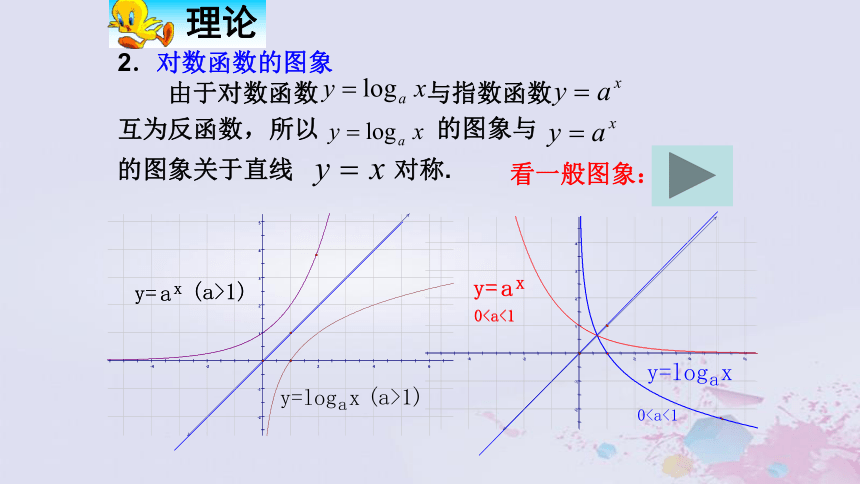
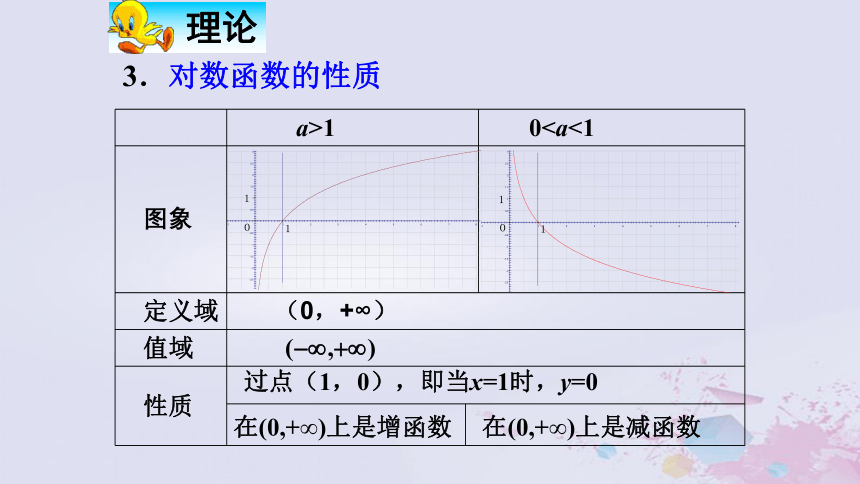
课件16张PPT。2.2.2 对数函数及其性质的图象和性质: 指数函数的图象和性质引例:有无反函数?若有,则求出.分析:观察图象知,有反函数由得所以,反函数为:1.对数函数的定义:函数 叫做对数函数(logarithmic fun_ction), 其中x是自变量,函数的定义域为 , 值域为 . 2.对数函数的图象由于对数函数 与指数函数 互为反函数, 所以 的图象与 的图象关于直线 对称. 看一般图象:3.对数函数的性质
(0,+∞)过点(1,0),即当x=1时,y=0 在(0,+∞)上是增函数在(0,+∞)上是减函数例1 求下列函数的定义域:解:(1)(2)由 得 ∴函数 的定义域是由 得 ∴函数 的定义域是(3)由 得 ∴函数 的定义域是例2 求下列函数的反函数解 :(1) (2) 例3 比较下列各组数中两个值的大小: 解:(1) (2) 考查对数函数 因为它的底数2>1,所以它在(0,+∞)上是增函数,于是 考查对数函数 因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,所以 1. 画出函数 的图象,并且说明这两个函数的相同性质和不同性质.解:相同性质: 两图象都位于y轴右方,
都经过点(1,0),这说
明两函数的定义域都是
(0,+∞),且当x=1, y=0.不同性质: 2.求下列函数的定义域:(1)(2)(3)(4) 对数函数的定义;
2. 对数函数的性质;
会利用对数函数的性质比较两个对
数函数的大小.
(0,+∞)过点(1,0),即当x=1时,y=0 在(0,+∞)上是增函数在(0,+∞)上是减函数例1 求下列函数的定义域:解:(1)(2)由 得 ∴函数 的定义域是由 得 ∴函数 的定义域是(3)由 得 ∴函数 的定义域是例2 求下列函数的反函数解 :(1) (2) 例3 比较下列各组数中两个值的大小: 解:(1) (2) 考查对数函数 因为它的底数2>1,所以它在(0,+∞)上是增函数,于是 考查对数函数 因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,所以 1. 画出函数 的图象,并且说明这两个函数的相同性质和不同性质.解:相同性质: 两图象都位于y轴右方,
都经过点(1,0),这说
明两函数的定义域都是
(0,+∞),且当x=1, y=0.不同性质: 2.求下列函数的定义域:(1)(2)(3)(4) 对数函数的定义;
2. 对数函数的性质;
会利用对数函数的性质比较两个对
数函数的大小.
