2018_2019学年高中数学第二章圆锥曲线与方程2.1.1椭圆及其标准方程课件新人教A版选修1_1(33张)
文档属性
| 名称 | 2018_2019学年高中数学第二章圆锥曲线与方程2.1.1椭圆及其标准方程课件新人教A版选修1_1(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 09:43:48 | ||
图片预览











文档简介
课件33张PPT。第二章 圆锥曲线与方程§2.1 椭圆
§2.1.1 椭圆及其标准方程
[课标解读]
1.了解椭圆的实际背景,经历从具体情境中抽象出椭圆的过程、椭圆标准方程的推导与化简过程.(难点)
2.掌握椭圆的定义、标准方程及几何图形.(重点、易错点)
1.椭圆的定义
(1)定义:平面内与两个定点F1,F2的距离之和等于_____ (大于|F1F2|)的点的轨迹.
(2)焦点:两个定点F1,F2.
(3)焦距:两焦点间的距离|F1F2|.
(4)几何表示:|MF1|+|MF2|=__ (常数)且2a__|F1F2|.
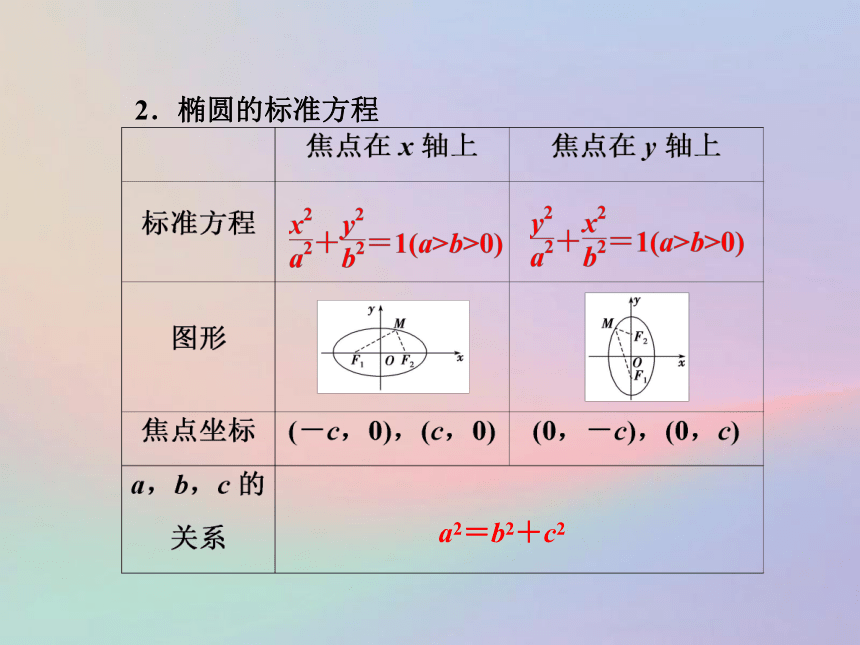
教材知识梳理常数2a>2.椭圆的标准方程
a2=b2+c2知识点一 椭圆的定义
探究1:通过探讨以下几个问题,初步形成对椭圆的认识.
(1)将一条细绳的两端用图钉分别固定在平面内的两个定点F1,F2上,用笔尖将细绳拉紧并运动,在纸上能得到怎样的图形?
提示 得到一个椭圆.
核心要点探究(2)如果调整细绳两端点F1,F2的相对位置,细绳的长度不变,猜想椭圆会发生怎样的变化?
提示 当细绳两端点逐步靠近时,所画的椭圆越接近圆,当细绳两端点逐步远离时,所画的椭圆越扁平.
(3)绳长能小于两图钉之间的距离吗?
提示 不能.
探究2:根据探究1中对椭圆的认识及椭圆的定义探讨以下问题:
(1)椭圆的定义中为什么要强调在平面内?
提示 去掉平面的限制后得到的是椭球体.
(2)如果已知椭圆方程及椭圆上一点到其中一个焦点的距离,能否得到它到另一焦点的距离?
提示 能,根据椭圆的定义,椭圆上的点到两定点的距离之和为常数,如果已知椭圆上一点到其中一个焦点的距离,可以求出它到另一个焦点的距离.
探究1:椭圆标准方程的推导过程遵循了求轨迹方程的哪些基本步骤,请完成下列填空.
(1)建立适当的坐标系,用有序实数对_______表示曲线上任意一点M的坐标;
(2)写出适合条件____;
(3)用坐标表示条件____,列出方程;
(4)化方程为最简形式.
(x,y)P(m)P(m)探究2:推导椭圆的标准方程过程中,对含有的两个根式是怎样处理的?
探究3:通过下列问题的探讨,进一步认识椭圆的标准方程.
(1)确定椭圆标准方程的关键是什么?
提示 确定参数a,b的值.
(2)求椭圆的标准方程时,设出椭圆方程的关键是什么?
提示 关键是先确定焦点的位置,若椭圆的焦点位置不能确定,要分别写出焦点在x轴、y轴上的椭圆的标准方程,不能遗漏.
题型一 求椭圆的标准方程例1●规律总结
1.求椭圆方程的方法
2.椭圆方程的设法技巧
若椭圆的焦点位置不确定,需要分焦点在x轴上和y轴上两种情况讨论,也可设椭圆的方程为mx2+ny2=1(m>0,n>0,m≠n).
◎变式训练题型二 椭圆的定义及其应用例2●规律总结
(1)椭圆的定义具有双向作用,即若|PF1|+|PF2|=2a(2a>|F1F2|),则点P的轨迹是椭圆;反之,椭圆上任意一点P到两焦点的距离之和必为2a.
(2)椭圆上一点P与椭圆的两个焦点F1,F2构成的△PF1F2,称为焦点三角形.解关于椭圆的焦点三角形的问题,通常要利用椭圆的定义,结合正弦定理、余弦定理等知识求解.
◎变式训练解析 ∵|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,
则△ABF2的周长=|AB|+|BF2|+|AF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a,∴△ABF2的周长为4a.
例3●规律总结
根据椭圆标准方程求参数取值问题的解题方法
(1)确定焦点的位置,从而可以得a2,b2的值.
(2)焦点不确定时,要进行分类讨论,分别求值.
(3)注意排除a2=b2,方程表示圆的情况.
◎对点训练易错误区(四) 对椭圆标准方程理解不清致误例1典题示例典题试解
§2.1.1 椭圆及其标准方程
[课标解读]
1.了解椭圆的实际背景,经历从具体情境中抽象出椭圆的过程、椭圆标准方程的推导与化简过程.(难点)
2.掌握椭圆的定义、标准方程及几何图形.(重点、易错点)
1.椭圆的定义
(1)定义:平面内与两个定点F1,F2的距离之和等于_____ (大于|F1F2|)的点的轨迹.
(2)焦点:两个定点F1,F2.
(3)焦距:两焦点间的距离|F1F2|.
(4)几何表示:|MF1|+|MF2|=__ (常数)且2a__|F1F2|.
教材知识梳理常数2a>2.椭圆的标准方程
a2=b2+c2知识点一 椭圆的定义
探究1:通过探讨以下几个问题,初步形成对椭圆的认识.
(1)将一条细绳的两端用图钉分别固定在平面内的两个定点F1,F2上,用笔尖将细绳拉紧并运动,在纸上能得到怎样的图形?
提示 得到一个椭圆.
核心要点探究(2)如果调整细绳两端点F1,F2的相对位置,细绳的长度不变,猜想椭圆会发生怎样的变化?
提示 当细绳两端点逐步靠近时,所画的椭圆越接近圆,当细绳两端点逐步远离时,所画的椭圆越扁平.
(3)绳长能小于两图钉之间的距离吗?
提示 不能.
探究2:根据探究1中对椭圆的认识及椭圆的定义探讨以下问题:
(1)椭圆的定义中为什么要强调在平面内?
提示 去掉平面的限制后得到的是椭球体.
(2)如果已知椭圆方程及椭圆上一点到其中一个焦点的距离,能否得到它到另一焦点的距离?
提示 能,根据椭圆的定义,椭圆上的点到两定点的距离之和为常数,如果已知椭圆上一点到其中一个焦点的距离,可以求出它到另一个焦点的距离.
探究1:椭圆标准方程的推导过程遵循了求轨迹方程的哪些基本步骤,请完成下列填空.
(1)建立适当的坐标系,用有序实数对_______表示曲线上任意一点M的坐标;
(2)写出适合条件____;
(3)用坐标表示条件____,列出方程;
(4)化方程为最简形式.
(x,y)P(m)P(m)探究2:推导椭圆的标准方程过程中,对含有的两个根式是怎样处理的?
探究3:通过下列问题的探讨,进一步认识椭圆的标准方程.
(1)确定椭圆标准方程的关键是什么?
提示 确定参数a,b的值.
(2)求椭圆的标准方程时,设出椭圆方程的关键是什么?
提示 关键是先确定焦点的位置,若椭圆的焦点位置不能确定,要分别写出焦点在x轴、y轴上的椭圆的标准方程,不能遗漏.
题型一 求椭圆的标准方程例1●规律总结
1.求椭圆方程的方法
2.椭圆方程的设法技巧
若椭圆的焦点位置不确定,需要分焦点在x轴上和y轴上两种情况讨论,也可设椭圆的方程为mx2+ny2=1(m>0,n>0,m≠n).
◎变式训练题型二 椭圆的定义及其应用例2●规律总结
(1)椭圆的定义具有双向作用,即若|PF1|+|PF2|=2a(2a>|F1F2|),则点P的轨迹是椭圆;反之,椭圆上任意一点P到两焦点的距离之和必为2a.
(2)椭圆上一点P与椭圆的两个焦点F1,F2构成的△PF1F2,称为焦点三角形.解关于椭圆的焦点三角形的问题,通常要利用椭圆的定义,结合正弦定理、余弦定理等知识求解.
◎变式训练解析 ∵|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,
则△ABF2的周长=|AB|+|BF2|+|AF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a,∴△ABF2的周长为4a.
例3●规律总结
根据椭圆标准方程求参数取值问题的解题方法
(1)确定焦点的位置,从而可以得a2,b2的值.
(2)焦点不确定时,要进行分类讨论,分别求值.
(3)注意排除a2=b2,方程表示圆的情况.
◎对点训练易错误区(四) 对椭圆标准方程理解不清致误例1典题示例典题试解
