2018_2019学年高中数学第三章数系的扩充与复数的引入3.1.1_3.1.2(一)实数系复数的引入(一)同步课件新人教B版选修1_2(30张)
文档属性
| 名称 | 2018_2019学年高中数学第三章数系的扩充与复数的引入3.1.1_3.1.2(一)实数系复数的引入(一)同步课件新人教B版选修1_2(30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 09:46:18 | ||
图片预览











文档简介
(共30张PPT)
3.1.1 实数系 3.1.2 复数的引入(一)
第三章 §3.1 数系的扩充与复数的引入
学习目标
1.了解引入虚数单位i的必要性和数集的扩充过程.
2.理解在数系的扩充中由实数集扩展到复数集出现的一些基本概念.
3.掌握复数代数形式的表示方法,理解复数相等的充要条件.
问题导学
达标检测
题型探究
内容索引
问题导学
知识点一 复数的概念及代数表示
思考 为解决方程x2=2在有理数范围内无根的问题,数系从有理数系扩充到实数系;那么怎样解决方程x2+1=0在实数系中无根的问题呢?
答案 设想引入新数i,使i是方程x2+1=0的根,即i·i=-1,方程x2+1=0有解,同时得到一些新数.
梳理 (1)复数的概念
设a,b都是实数,形如
的数叫做复数.
(2)复数的表示
复数通常用小写字母z表示,即z=
(a,b∈R),其中a叫做复数z的
,b叫做复数z的
,i称作
.
a+bi
a+bi
实部
虚部
虚数单位
知识点二 复数的分类与复数相等的充要条件
思考1 复数z=a+bi(a,b∈R),当b=0时,z是什么数?
思考2 复数z=a+bi(a,b∈R),当a=0且b≠0时,z是什么数?
答案 实数.
答案 纯虚数.
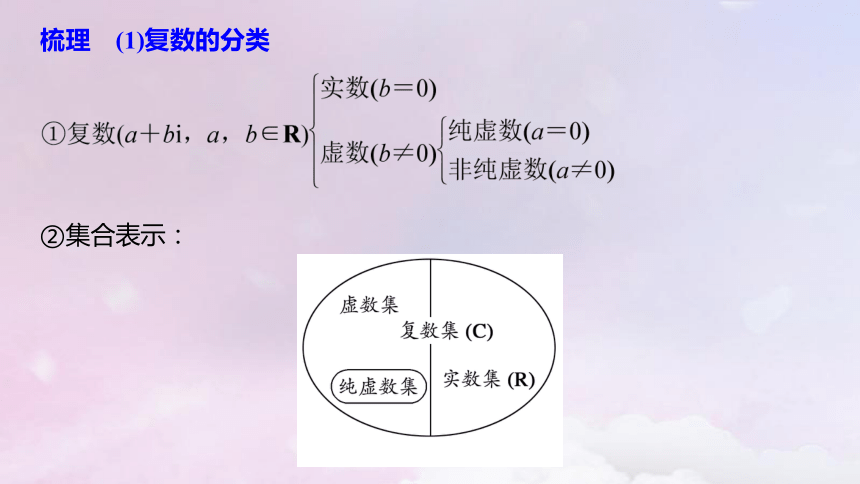
梳理 (1)复数的分类
②集合表示:
(2)复数相等的充要条件
如果a,b,c,d都是实数,那么a+bi=c+di
;a+bi=0
.
a=c,且b=d
a=0,且b=0
1.若a,b为实数,则z=a+bi为虚数.( )
2.复数z=bi是纯虚数.( )
3.若两个复数的实部的差和虚部的差都等于0,那么这两个复数相等.
( )
[思考辨析
判断正误]
×
×
√
题型探究
例1 当实数m满足什么条件时,复数lg(m2-2m-7)+(m2+5m+6)i:
(1)是纯虚数;
类型一 复数的概念与分类
解答
解得m=4.
(2)是实数;
解答
解得m=-2或m=-3.
(3)是虚数.
解答
反思与感悟 利用复数的代数形式对复数分类时,关键是根据分类标准列出实部、虚部应满足的关系式(等式或不等式(组)),求解参数时,注意参数本身的取值范围,如分母不能为0.
即m-1≠0,解得m=-3.
解答
(2)虚数;
解答
即m-1≠0,解得m≠1且m≠-3.
(3)纯虚数.
且m2+2m-3≠0,
解得m=0或m=-2.
例2 (1)已知x2-y2+2xyi=2i,求实数x,y的值;
类型二 复数相等
解答
解 ∵x2-y2+2xyi=2i,
解答
解 设方程的实数根为x=m,则原方程可变为
反思与感悟 两个复数相等,首先要分清两复数的实部与虚部,然后利用两个复数相等的充要条件可得到两个方程,从而可以确定两个独立参数.
跟踪训练2 已知M={1,(m2-2m)+(m2+m-2)i},P={-1,1,4i},若M∪P=P,求实数m的值.
解答
解 ∵M∪P=P,∴M P,
∴(m2-2m)+(m2+m-2)i=-1或(m2-2m)+(m2+m-2)i=4i.
由(m2-2m)+(m2+m-2)i=-1,得
由(m2-2m)+(m2+m-2)i=4i,得
综上可知m=1或m=2.
达标检测
1
2
3
4
1.下列复数中,满足方程x2+2=0的是
A.±1
B.±i
C.
D.±2i
答案
√
5
2.若(x2-1)+(x2+3x+2)i是纯虚数,则实数x的值是
A.1
B.-1
C.±1
D.以上都不对
解析 因为(x2-1)+(x2+3x+2)i是纯虚数,所以x2-1=0且x2+3x+2≠0,解得x=1,故选A.
解析
答案
√
1
2
3
4
5
3.下列几个命题:
①两个复数相等的一个必要条件是它们的实部相等;
②两个复数不相等的一个充分条件是它们的虚部不相等;
③1-ai(a∈R)是一个复数;
④虚数的平方不小于0;
⑤-1的平方根只有一个,即为-i;
⑥i是方程x4-1=0的一个根;
⑦
是一个无理数.
其中真命题的个数为
A.3
B.4
C.5
D.6
√
解析
答案
1
2
3
4
5
解析 命题①②③⑥正确,④⑤⑦错误.
4.复数4-3a-a2i与复数a2+4ai相等,则实数a=________.
1
2
3
4
5
-4
解析
答案
1
2
3
4
5
2-2i
∴新复数z=2-2i.
解析
答案
1.区分实数、虚数、纯虚数与复数的关系,特别要明确:实数也是复数,要把复数与实数加以区别.对于纯虚数bi(b≠0,b∈R)不要只记形式,要注意b≠0.
2.应用两复数相等的充要条件时,首先要把等号左右两边的复数写成代数形式,即分离实部与虚部,然后列出等式求解.
3.若两个复数全是实数,则可以比较大小,反之,若两个复数能比较大小,则它们必是实数.
规律与方法
本课结束
3.1.1 实数系 3.1.2 复数的引入(一)
第三章 §3.1 数系的扩充与复数的引入
学习目标
1.了解引入虚数单位i的必要性和数集的扩充过程.
2.理解在数系的扩充中由实数集扩展到复数集出现的一些基本概念.
3.掌握复数代数形式的表示方法,理解复数相等的充要条件.
问题导学
达标检测
题型探究
内容索引
问题导学
知识点一 复数的概念及代数表示
思考 为解决方程x2=2在有理数范围内无根的问题,数系从有理数系扩充到实数系;那么怎样解决方程x2+1=0在实数系中无根的问题呢?
答案 设想引入新数i,使i是方程x2+1=0的根,即i·i=-1,方程x2+1=0有解,同时得到一些新数.
梳理 (1)复数的概念
设a,b都是实数,形如
的数叫做复数.
(2)复数的表示
复数通常用小写字母z表示,即z=
(a,b∈R),其中a叫做复数z的
,b叫做复数z的
,i称作
.
a+bi
a+bi
实部
虚部
虚数单位
知识点二 复数的分类与复数相等的充要条件
思考1 复数z=a+bi(a,b∈R),当b=0时,z是什么数?
思考2 复数z=a+bi(a,b∈R),当a=0且b≠0时,z是什么数?
答案 实数.
答案 纯虚数.
梳理 (1)复数的分类
②集合表示:
(2)复数相等的充要条件
如果a,b,c,d都是实数,那么a+bi=c+di
;a+bi=0
.
a=c,且b=d
a=0,且b=0
1.若a,b为实数,则z=a+bi为虚数.( )
2.复数z=bi是纯虚数.( )
3.若两个复数的实部的差和虚部的差都等于0,那么这两个复数相等.
( )
[思考辨析
判断正误]
×
×
√
题型探究
例1 当实数m满足什么条件时,复数lg(m2-2m-7)+(m2+5m+6)i:
(1)是纯虚数;
类型一 复数的概念与分类
解答
解得m=4.
(2)是实数;
解答
解得m=-2或m=-3.
(3)是虚数.
解答
反思与感悟 利用复数的代数形式对复数分类时,关键是根据分类标准列出实部、虚部应满足的关系式(等式或不等式(组)),求解参数时,注意参数本身的取值范围,如分母不能为0.
即m-1≠0,解得m=-3.
解答
(2)虚数;
解答
即m-1≠0,解得m≠1且m≠-3.
(3)纯虚数.
且m2+2m-3≠0,
解得m=0或m=-2.
例2 (1)已知x2-y2+2xyi=2i,求实数x,y的值;
类型二 复数相等
解答
解 ∵x2-y2+2xyi=2i,
解答
解 设方程的实数根为x=m,则原方程可变为
反思与感悟 两个复数相等,首先要分清两复数的实部与虚部,然后利用两个复数相等的充要条件可得到两个方程,从而可以确定两个独立参数.
跟踪训练2 已知M={1,(m2-2m)+(m2+m-2)i},P={-1,1,4i},若M∪P=P,求实数m的值.
解答
解 ∵M∪P=P,∴M P,
∴(m2-2m)+(m2+m-2)i=-1或(m2-2m)+(m2+m-2)i=4i.
由(m2-2m)+(m2+m-2)i=-1,得
由(m2-2m)+(m2+m-2)i=4i,得
综上可知m=1或m=2.
达标检测
1
2
3
4
1.下列复数中,满足方程x2+2=0的是
A.±1
B.±i
C.
D.±2i
答案
√
5
2.若(x2-1)+(x2+3x+2)i是纯虚数,则实数x的值是
A.1
B.-1
C.±1
D.以上都不对
解析 因为(x2-1)+(x2+3x+2)i是纯虚数,所以x2-1=0且x2+3x+2≠0,解得x=1,故选A.
解析
答案
√
1
2
3
4
5
3.下列几个命题:
①两个复数相等的一个必要条件是它们的实部相等;
②两个复数不相等的一个充分条件是它们的虚部不相等;
③1-ai(a∈R)是一个复数;
④虚数的平方不小于0;
⑤-1的平方根只有一个,即为-i;
⑥i是方程x4-1=0的一个根;
⑦
是一个无理数.
其中真命题的个数为
A.3
B.4
C.5
D.6
√
解析
答案
1
2
3
4
5
解析 命题①②③⑥正确,④⑤⑦错误.
4.复数4-3a-a2i与复数a2+4ai相等,则实数a=________.
1
2
3
4
5
-4
解析
答案
1
2
3
4
5
2-2i
∴新复数z=2-2i.
解析
答案
1.区分实数、虚数、纯虚数与复数的关系,特别要明确:实数也是复数,要把复数与实数加以区别.对于纯虚数bi(b≠0,b∈R)不要只记形式,要注意b≠0.
2.应用两复数相等的充要条件时,首先要把等号左右两边的复数写成代数形式,即分离实部与虚部,然后列出等式求解.
3.若两个复数全是实数,则可以比较大小,反之,若两个复数能比较大小,则它们必是实数.
规律与方法
本课结束
