北师大版八年级下册数学同步练习卷: 4.3 公式法(含答案)
文档属性
| 名称 | 北师大版八年级下册数学同步练习卷: 4.3 公式法(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 43.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-26 10:02:42 | ||
图片预览


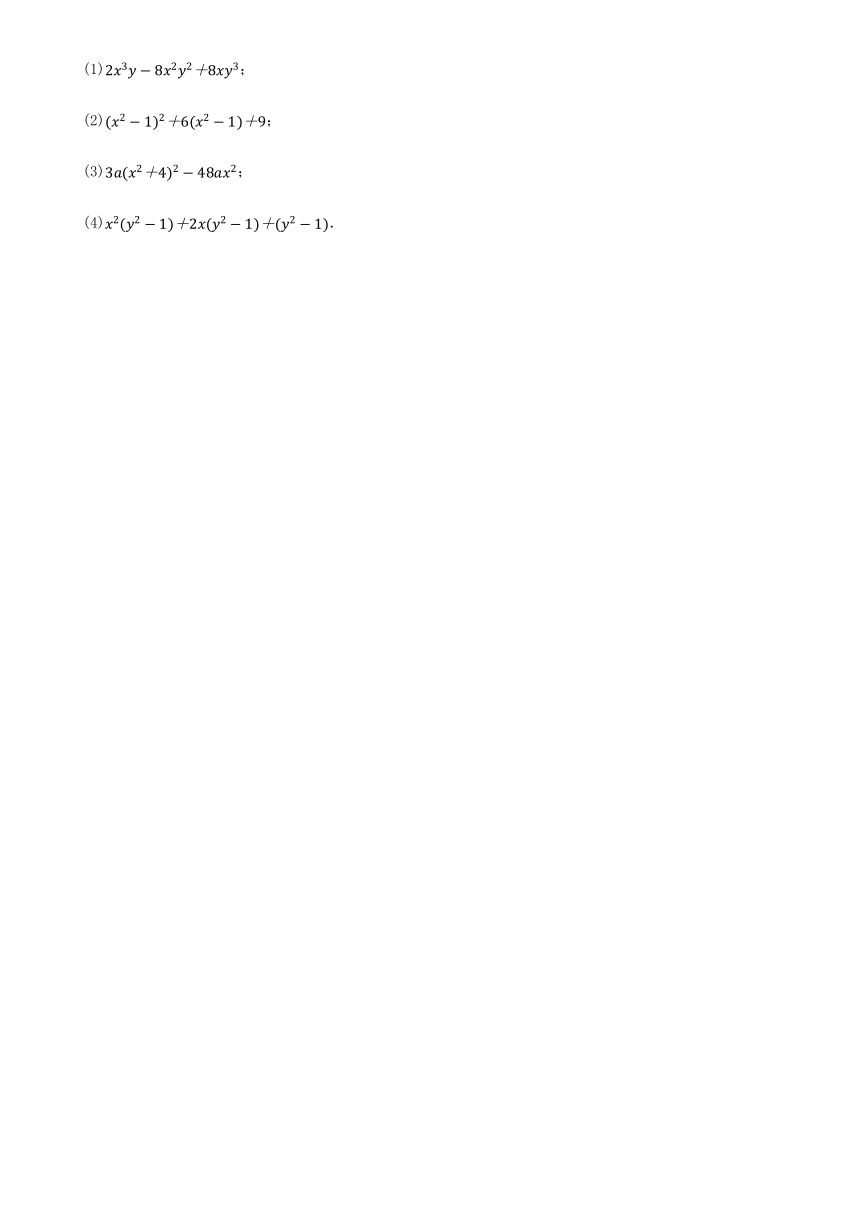

文档简介
4.3 公式法
一、填空题
下列多项式中,能运用公式法因式分解的有? ? ? ? ? ? ? ? ? ??.
①-a2+b2;②4x2+4x+1;③-x2-y2;④-x2+8x-16;⑤x4-1;⑥m2+4m-4.
利用乘法公式计算:(___________+__________)2=982+4×98+4=____________.
若可用完全平方公式法进行因式分解,则m=? ? ??.
把乘法公式(a+b)(a-b)=________反过来就得到___________________.
把多项式ax2+2a2x+a3分解因式的结果是______.
因式分解:a2b-4ab+4b=______.
分解因式:(m+1)(m-9)+8m= ______ .
若多项式能用完全平方公式因式分解,则m的值为______.
因式分解:-2x2y+12xy-18y=______.
已知a(a-1)-(a2-b)=1,求的值______ .
二、选择题
解方程(x+5)2-3(x+5)=0,较简便的方法是()
A. 直接开平方法 B. 因式分解法 C. 配方法 D. 公式法
下列多项式中,能用公式法分解因式的是( )
A. B. C. D.
将3a(x-y)-b(x-y)用提公因式法分解因式,提出的公因式是( )
A. B. C. D.
下列多项式中,不能用公式法分解因式的是( )
A. B.
C. D.
多项式x2-kx+9能用公式法分解因式,则k的值为( )
A. B. 3 C. D. 6
如果a2+16与一个单项式的和可以用完全平方公式法分解因式,那么这个单项式可以是(??? )
A. 4a B. C. D.
下列各式的分解因式中,没有用到公式法的是( )
A. B.
C. D.
多项式x2+x提取公因式x后的另一个因式是(??? ).
A. B. x C. D.
下列各式中,能运用两数和(差)的平方公式进行因式分解的是()
A. B. C. D.
下列各多项式中,能运用公式法分解因式的有()
①②③④
⑤⑥⑦
A. 4个 B. 5个 C. 6个 D. 7个
三、计算题
利用公式简算:
(1)2008+20082-20092;
(2)3.14×512-3.14×492.
运用公式法因式分解:
(1);
(2);
(3);
(4).
答案
1.【答案】①②④⑤
【解答】
解:①⑤能用平方差公式分解;②④能用完全平方公式分解.
故答案为①②④⑤.
2.【答案】98;2;10000
解:原式=982+2×98×2+22=(98+2)2=1002?=10000,
故答案为?98;2;10000.
3.【答案】
解:由题意知是完全平方式,
所以,
则.
故答案为.
4.【答案】a2-b2;a2-b2=(a+b)(a-b)
解:∵(a+b)(a-b)=a2-b2,
∴a2-b2=(a+b)(a-b).
故答案为a2-b2;a2-b2=(a+b)(a-b).
5.【答案】a(x+a)2
【解析】
解:ax2+2a2x+a3
=a(x2+2ax+a2)
=a(x+a)2,
故答案为:a(x+a)2
6.【答案】b(a-2)2
解:原式=b(a2-4a+4)=b(a-2)2.
故答案为b(a-2)2.
7.【答案】(m+3)(m-3)
【解析】
解:(m+1)(m-9)+8m,
=m2-9m+m-9+8m,
=m2-9,
=(m+3)(m-3).
故答案为:(m+3)(m-3).
8.【答案】7或-3
【解析】
解:∵多项式x2+2(m-2)x+25能用完全平方公式因式分解,
∴2(m-2)=±10,
解得:m=7或-3,
故答案为:7或-3.
9.【答案】-2y(x-3)2
【解析】
解:原式=-2y(x2-6x+9)
=-2y(x-3)2.
故答案为:-2y(x-3)2.
10.【答案】
【解析】
解:∵a(a-1)-(a2-b)=a2-a-a2+b=1,
∴a-b=-1,
则原式=(a2+b2-2ab)=(a-b)2=.
故答案为:.
11.【答案】B
解:
(x+5)2-3(x+5)=0,
提取公因式(x+5)(x+5-3)=0,
解得x1=-5,x2=-2.
故较简便的方法是因式分解法.
故选B.
12.【答案】D
解:A.不能用因式分解;
B.不能用完全平方公式;
C.不能因式分解,
D.能因式分解,-m2+n2=(n+m)(n-m).
?故选D.
13.【答案】C
【解析】
解:3a(x-y)-b(x-y)
=(x-y)(3a-b).
故选:C.
14.【答案】C
解:A.原式=(x+y+6)2,不合题意;
B.原式=-(x-y)2,不合题意;
C.原式不能分解,符合题意;
D.原式=(3y+2x)(3y-2x),不合题意.
故选C.
15.【答案】C
【解析】
解:∵多项式x2-kx+9能用公式法分解因式,并且它有三项,
∴它是一个完全平方式,
∴这两个数是3、x,
∴k=±2×3=±6.
故选:C.
16.【答案】B
解:根据完全平方公式(a±b)2=a2±2ab+b2,
由a2+16,得a2+16=a2+42,
对比(a±b)2=a2±2ab+b2,可得b=4,2ab=2a×4=8a,
所以这个单项式为±8a.
?故选B.
17.【答案】B
【解析】
解:A、提公因式法,完全平方公式,故A正确;
B、提公因式法,故B错误;
C、提公因式法,平方差公式,故C正确;
D、完全平方公式,故D正确;
故选:B.
18.【答案】D
【解析】
略
19.【答案】B
解:A.不能用平方差公式分解因式,故该选项错误;
B.能用平方公式分解因式,=(a+2b)(a-2b),故该选项正确;
C.不可以用平方差公式分解原式,故该选项错误;
D.不能用平方差公式分解因式,故该选项错误;
故选B.
20.【答案】B
【解析】
解:①-m2+4=(2+m)(2-m),符合题意;
②-x2-y2=-(x2+y2),不符合题意;
③x2y2-1=(xy+1)(xy-1),符合题意;
④(m-a)2-(m+a)2=(m-a+m+a)(m-a-m-a)=-4ma,符合题意;
⑤2x2-8y2=2(x2-4y2)=2(x+2y)(x-2y),符合题意;
⑥-x2-2xy-y2=-(x2+2xy+y2)=-(x+y)2,符合题意;
⑦9a2b2-3ab+1,不符合题意.
符合题意的有5个.
故选B.
21.【答案】解:(1)2008+20082-20092=2008+(2008+2009)(2008-2009)
=2008-(2008+2009)
=-2009.
(2)3.14×512-3.14×492= 3.14×(512-492)
=3.14×(51+49)(51-49)
=3.14×100×2
=628.
22.【答案】解:(1);
(2)原式=.
(3)=.
?(4).
一、填空题
下列多项式中,能运用公式法因式分解的有? ? ? ? ? ? ? ? ? ??.
①-a2+b2;②4x2+4x+1;③-x2-y2;④-x2+8x-16;⑤x4-1;⑥m2+4m-4.
利用乘法公式计算:(___________+__________)2=982+4×98+4=____________.
若可用完全平方公式法进行因式分解,则m=? ? ??.
把乘法公式(a+b)(a-b)=________反过来就得到___________________.
把多项式ax2+2a2x+a3分解因式的结果是______.
因式分解:a2b-4ab+4b=______.
分解因式:(m+1)(m-9)+8m= ______ .
若多项式能用完全平方公式因式分解,则m的值为______.
因式分解:-2x2y+12xy-18y=______.
已知a(a-1)-(a2-b)=1,求的值______ .
二、选择题
解方程(x+5)2-3(x+5)=0,较简便的方法是()
A. 直接开平方法 B. 因式分解法 C. 配方法 D. 公式法
下列多项式中,能用公式法分解因式的是( )
A. B. C. D.
将3a(x-y)-b(x-y)用提公因式法分解因式,提出的公因式是( )
A. B. C. D.
下列多项式中,不能用公式法分解因式的是( )
A. B.
C. D.
多项式x2-kx+9能用公式法分解因式,则k的值为( )
A. B. 3 C. D. 6
如果a2+16与一个单项式的和可以用完全平方公式法分解因式,那么这个单项式可以是(??? )
A. 4a B. C. D.
下列各式的分解因式中,没有用到公式法的是( )
A. B.
C. D.
多项式x2+x提取公因式x后的另一个因式是(??? ).
A. B. x C. D.
下列各式中,能运用两数和(差)的平方公式进行因式分解的是()
A. B. C. D.
下列各多项式中,能运用公式法分解因式的有()
①②③④
⑤⑥⑦
A. 4个 B. 5个 C. 6个 D. 7个
三、计算题
利用公式简算:
(1)2008+20082-20092;
(2)3.14×512-3.14×492.
运用公式法因式分解:
(1);
(2);
(3);
(4).
答案
1.【答案】①②④⑤
【解答】
解:①⑤能用平方差公式分解;②④能用完全平方公式分解.
故答案为①②④⑤.
2.【答案】98;2;10000
解:原式=982+2×98×2+22=(98+2)2=1002?=10000,
故答案为?98;2;10000.
3.【答案】
解:由题意知是完全平方式,
所以,
则.
故答案为.
4.【答案】a2-b2;a2-b2=(a+b)(a-b)
解:∵(a+b)(a-b)=a2-b2,
∴a2-b2=(a+b)(a-b).
故答案为a2-b2;a2-b2=(a+b)(a-b).
5.【答案】a(x+a)2
【解析】
解:ax2+2a2x+a3
=a(x2+2ax+a2)
=a(x+a)2,
故答案为:a(x+a)2
6.【答案】b(a-2)2
解:原式=b(a2-4a+4)=b(a-2)2.
故答案为b(a-2)2.
7.【答案】(m+3)(m-3)
【解析】
解:(m+1)(m-9)+8m,
=m2-9m+m-9+8m,
=m2-9,
=(m+3)(m-3).
故答案为:(m+3)(m-3).
8.【答案】7或-3
【解析】
解:∵多项式x2+2(m-2)x+25能用完全平方公式因式分解,
∴2(m-2)=±10,
解得:m=7或-3,
故答案为:7或-3.
9.【答案】-2y(x-3)2
【解析】
解:原式=-2y(x2-6x+9)
=-2y(x-3)2.
故答案为:-2y(x-3)2.
10.【答案】
【解析】
解:∵a(a-1)-(a2-b)=a2-a-a2+b=1,
∴a-b=-1,
则原式=(a2+b2-2ab)=(a-b)2=.
故答案为:.
11.【答案】B
解:
(x+5)2-3(x+5)=0,
提取公因式(x+5)(x+5-3)=0,
解得x1=-5,x2=-2.
故较简便的方法是因式分解法.
故选B.
12.【答案】D
解:A.不能用因式分解;
B.不能用完全平方公式;
C.不能因式分解,
D.能因式分解,-m2+n2=(n+m)(n-m).
?故选D.
13.【答案】C
【解析】
解:3a(x-y)-b(x-y)
=(x-y)(3a-b).
故选:C.
14.【答案】C
解:A.原式=(x+y+6)2,不合题意;
B.原式=-(x-y)2,不合题意;
C.原式不能分解,符合题意;
D.原式=(3y+2x)(3y-2x),不合题意.
故选C.
15.【答案】C
【解析】
解:∵多项式x2-kx+9能用公式法分解因式,并且它有三项,
∴它是一个完全平方式,
∴这两个数是3、x,
∴k=±2×3=±6.
故选:C.
16.【答案】B
解:根据完全平方公式(a±b)2=a2±2ab+b2,
由a2+16,得a2+16=a2+42,
对比(a±b)2=a2±2ab+b2,可得b=4,2ab=2a×4=8a,
所以这个单项式为±8a.
?故选B.
17.【答案】B
【解析】
解:A、提公因式法,完全平方公式,故A正确;
B、提公因式法,故B错误;
C、提公因式法,平方差公式,故C正确;
D、完全平方公式,故D正确;
故选:B.
18.【答案】D
【解析】
略
19.【答案】B
解:A.不能用平方差公式分解因式,故该选项错误;
B.能用平方公式分解因式,=(a+2b)(a-2b),故该选项正确;
C.不可以用平方差公式分解原式,故该选项错误;
D.不能用平方差公式分解因式,故该选项错误;
故选B.
20.【答案】B
【解析】
解:①-m2+4=(2+m)(2-m),符合题意;
②-x2-y2=-(x2+y2),不符合题意;
③x2y2-1=(xy+1)(xy-1),符合题意;
④(m-a)2-(m+a)2=(m-a+m+a)(m-a-m-a)=-4ma,符合题意;
⑤2x2-8y2=2(x2-4y2)=2(x+2y)(x-2y),符合题意;
⑥-x2-2xy-y2=-(x2+2xy+y2)=-(x+y)2,符合题意;
⑦9a2b2-3ab+1,不符合题意.
符合题意的有5个.
故选B.
21.【答案】解:(1)2008+20082-20092=2008+(2008+2009)(2008-2009)
=2008-(2008+2009)
=-2009.
(2)3.14×512-3.14×492= 3.14×(512-492)
=3.14×(51+49)(51-49)
=3.14×100×2
=628.
22.【答案】解:(1);
(2)原式=.
(3)=.
?(4).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
