江西省瑞金市人教版八年级下册第二十章数据的分析单元检测题(含答案)
文档属性
| 名称 | 江西省瑞金市人教版八年级下册第二十章数据的分析单元检测题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 403.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-26 00:00:00 | ||
图片预览


文档简介
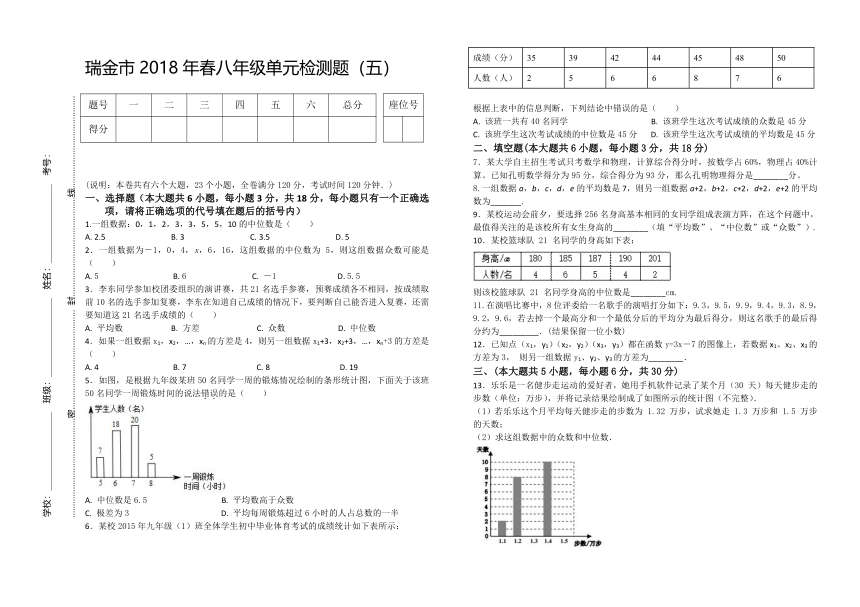
瑞金市2018年春八年级单元检测题(五)
题号
一
二
三
四
五
六
总分
得分
座位号
(说明:本卷共有六个大题,23个小题,全卷满分120分,考试时间120分钟.)
选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项,请将正确选项的代号填在题后的括号内)
1.一组数据:0,1,2,3,3,5,5,10的中位数是( )
A. 2.5 B. 3 C. 3.5 D. 5
2.一组数据为-1,0,4,x,6,16,这组数据的中位数为 5,则这组数据众数可能是( )
A. 5 B. 6 C. -1 D. 5.5
3.李东同学参加校团委组织的演讲赛,共21名选手参赛,预赛成绩各不相同,按成绩取前10名的选手参加复赛,李东在知道自己成绩的情况下,要判断自己能否进入复赛,还需要知道这21名选手成绩的( )
A. 平均数 B. 方差 C. 众数 D. 中位数
4.如果一组数据x1,x2,…,xn的方差是4,则另一组数据x1+3,x2+3,…,xn+3的方差是( )
A. 4 B. 7 C. 8 D. 19
5.如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
A. 中位数是6.5 B. 平均数高于众数
C. 极差为3 D. 平均每周锻炼超过6小时的人占总数的一半
6.某校2015年九年级(1)班全体学生初中毕业体育考试的成绩统计如下表所示:
成绩(分)
35
39
42
44
45
48
50
人数(人)
2
5
6
6
8
7
6
根据上表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学 B. 该班学生这次考试成绩的众数是45分
C. 该班学生这次考试成绩的中位数是45分 D. 该班学生这次考试成绩的平均数是45分
二、填空题(本大题共6小题,每小题3分,共18分)
某大学自主招生考试只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算。已知孔明数学得分为95分,综合得分为93分,那么孔明物理得分是________分。
8.一组数据a,b,c,d,e的平均数是7,则另一组数据a+2,b+2,c+2,d+2,e+2的平均数为_______.
9.某校运动会前夕,要选择256名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的________(填“平均数”、“中位数”或“众数”).
10.某校篮球队 21 名同学的身高如下表:
则该校篮球队 21 名同学身高的中位数是________cm.
11.在演唱比赛中,8位评委给一名歌手的演唱打分如下:9.3,9.5,9.9,9.4,9.3,8.9,9.2,9.6,若去掉一个最高分和一个最低分后的平均分为最后得分,则这名歌手的最后得分约为_________.(结果保留一位小数)
12.已知点(x1,y1)(x2,y2)(x3,y3)都在函数y=3x-7的图像上,若数据x1、x2、x3的方差为3, 则另一组数据y1、y2、y3的方差为________.
三、(本大题共5小题,每小题6分,共30分)
13.乐乐是一名健步走运动的爱好者,她用手机软件记录了某个月(30 天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
(1)若乐乐这个月平均每天健步走的步数为 1.32 万步,试求她走 1.3 万步和 1.5 万步的天数;
(2)求这组数据中的众数和中位数.
14.某车间为了改变管理松懈的状况,准备采取每天任务定额和超产有奖的措施,从而提高工作效率.下面是该车间15名工人过去一天中各自装配机器的数量(单位:台):
15,6,16,7,15,8,7,13,8,11,8,10,9,10,9.
请回答下列问题:
(1)这组数据的平均数、众数和中位数各是多少(结果精确到0.01台)?
(2)管理者应确定每人标准日产量为多少台比较合适?
15.一家面临倒闭的企业在“调整产业结构,转变经营机制”的改革后,扭亏为盈. 下表是该企业2015年8~12月、2016年第一季度的月利润统计表:
根据以上信息,解答下列问题:
(1)2015年8月至2016年1月该企业利润的月平均利润为____万元,月利润的中位数为_____万元;
已知该企业2016年2、3月份的月利润的平均增长率相同,求这个平均增长率和2月份的月利润.
16.王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
17.学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手
表达能力
阅读理解
综合素质
汉字听写
甲
85
78
85
73
乙
73
80
82
83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
四、(本大题共3小题,每小题8分,共24分)
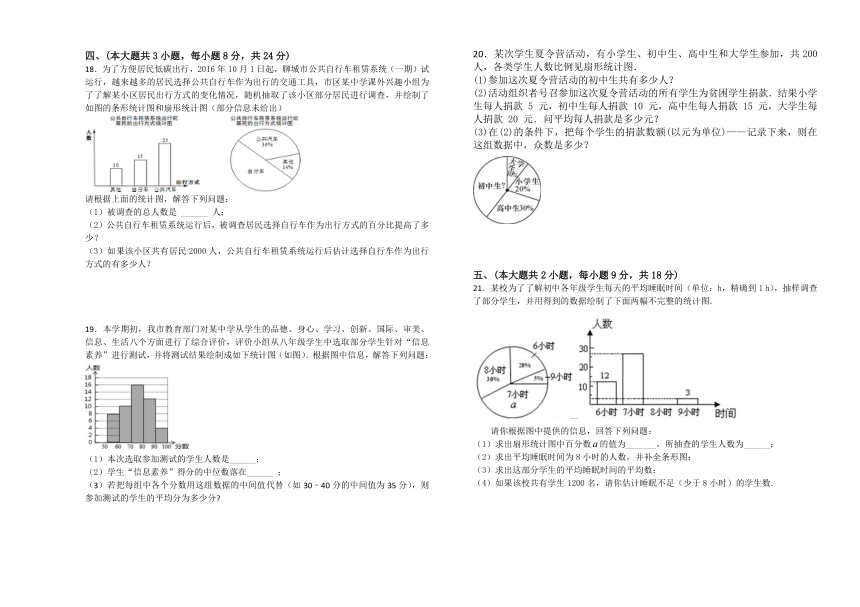
18.为了方便居民低碳出行,2016年10月1日起,聊城市公共自行车租赁系统(一期)试运行,越来越多的居民选择公共自行车作为出行的交通工具,市区某中学课外兴趣小组为了了解某小区居民出行方式的变化情况,随机抽取了该小区部分居民进行调查,并绘制了如图的条形统计图和扇形统计图(部分信息未给出)
请根据上面的统计图,解答下列问题:
(1)被调查的总人数是 ______ 人;
(2)公共自行车租赁系统运行后,被调查居民选择自行车作为出行方式的百分比提高了多少?
(3)如果该小区共有居民2000人,公共自行车租赁系统运行后估计选择自行车作为出行方式的有多少人?
19.本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
(1)本次选取参加测试的学生人数是______;
(2)学生“信息素养”得分的中位数落在______ ;
(3)若把每组中各个分数用这组数据的中间值代替(如30﹣40分的中间值为35分),则参加测试的学生的平均分为多少分?
20.某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款 5 元,初中生每人捐款 10 元,高中生每人捐款 15 元,大学生每人捐款 20 元.问平均每人捐款是多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)——记录下来,则在这组数据中,众数是多少?
五、(本大题共2小题,每小题9分,共18分)
21.某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数的值为_______,所抽查的学生人数为______;
(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
22.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
(1)在图①中,“80分”所在扇形的圆心角度数为 ;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
六、(本大题共12分)
23.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
1
乙
5.4
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
(五)
一.1.B 2.B 3.D 4.A 5.B 6.D
二.7. 90分8. 9 9. 众数10.187 11.9.4 12. 27
三.13.(1)6天,4天;(2)众数是1.4万步,中位数为1.3万步
【解析】(1)设乐乐有天每天走1.3万步,有天每天走1.5万步,
则 解得
即乐乐有6天每天走1.3万步,有4天每天走1.5万步.
(2)众数是1.4万步,中位数为1.3万步.
14.(1)平均数是10.13台;中位数是9台;众数是8台(2)管理者应确定每人标准日产量为9台比较合适
试题解析:(1)平均数是 (15+6+16+7+15+8+7+13+8+11+8+10+9+10+9)≈10.13(台);中位数是9台;众数是8台.
(2)管理者应确定每人标准日产量为9台比较合适.
因为:若规定8台,则大多数工人不需要努力就可以完成任务,不利于促进生产;
若规定10台为标准日产量,则多数工人不可能超过,甚至还完不成定额,回挫伤生产积极性,比较合理的生产定额应该确定在恰好能使多数人有超过的能力,因此取中位数9台比较合适。
15.(1)45,45;(2)2月份利润为60万元.
试题解析:(1)2015年8月至2016年1月该企业利润的月平均利润为 45 万元,月利润的中位数为 45 万元;
(2)设该企业月平均增长率为x,则
50(1+x)2=72
x=0.2或-2.2(舍去)
∴2月份利润:50(1+0.2)=60万元
16.(1)7840千克;(2)乙山上的杨梅产量较稳定.
试题解析:(1)甲山上4棵树的产量分别为:50千克、36千克、40千克、34千克,
所以甲山产量的样本平均数为: 千克;
乙山上4棵树的产量分别为:36千克、40千克、48千克、36千克,
所以乙山产量的样本平均数为千克.
总产量为40×100×98%×2=7840(千克)
答:甲、乙两片山上杨梅产量数样本的平均数分别为:40kg,40kg;
(2)由题意,得
S甲2=(千克2);
S乙2=(千克2)
∵38>24
∴S2甲>S2乙
∴乙山上的杨梅产量较稳定.
17.甲;乙
解:(1)=(73+80+82+83)÷4=79.5,
∵80.25>79.5,
∴应选派甲;
(2)=(85×2+78×1+85×3+73×4)÷(2+1+3+4)=79.5,
=(73×2+80×1+82×3+83×4)÷(2+1+3+4)=80.4,
∵79.5<80.4,
∴应选派乙.
四.18.(1)50;(2)20%;(3)1000人
试题解析:(1)由条形图可知,被调查的总人数是10+15+25=50人,
(2)共自行车租公赁系统运行前,居民选择自行车作为出行方式的百分比为:15÷50=30%,
公共自行车租赁系统运行后,居民选择自行车作为出行方式的百分比为:100%-36%-14%=50%,
50%-30%=20%,
答:公共自行车租赁系统运行后,被调查居民选择自行车作为出行方式的百分比提高了20%;
(3)公共自行车租赁系统运行后估计选择自行车作为出行方式的有:2000×50%=1000人.
19.(1)50人;
(2)70分~80分组;
(3)参加测试的学生的平均分为73.8分.
试题解析:(1)8+10+16+12+4=50;
(2)学生“信息素养”得分的中位数是70分~80分组;
(3)(8×55+10×65+16×75+12×85+4×95)÷50=3690÷50=73.8(分)
答:参加测试的学生的平均分为73.8分。
20.(1)80 人;(2)11.5 元; (3)10 元.
试题解析:解:(1)参加这次夏令营活动的初中生共有200×(1-10%-20%-30%)=80人; (2)小学生、高中生和大学生的人数为200×20%=40,200×30%=60,200×10%=20, 所以平均每人捐款==11.5(元); (3)因为初中生最多,所以众数为10(元).
五.21.(1)45% ,60人;(2)补全图见解析;(3)7.2小时;(4)780人.
【解析】(1)45% ,60人;
(2)平均睡眠时间为8小时的人数为60×30%=18人,补全图例如下
(3)这部分学生的平均睡眠时间的平均数为7.2小时;
(4)∵抽取的60名学生中,睡眠时间在8小时以下的有12+27=39人,
∴1200名学生中睡眠不足的有×1200=780人.
22.(1)54°;(2)补图见解析;(3)85分;(4)甲班20同名同学的成绩比较整齐.
试题解析:(1)6÷30%=20,
3÷20=15%,
360°×15%=54°;
(2)20-6-3-6=5,统计图补充如下:
(3)20-1-7-8=4,
=85;
(4)∵S甲2<S乙2,
∴甲班20同名同学的成绩比较整齐.
六.23.【解析】(1)根据平均数、中位数、方差的求法.
(2)①平均数相同的情况下,比较方差看谁更为稳定.
②乙的中位数比甲大,说明乙中间水平比甲高.
③乙命中9环以上的次数是3次,而甲只有一次.
④从折线统计图上看,乙在不断地上升,并且得到较高环次数也较多,说明乙具备潜力.
(1)如表
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
7
1
乙
7
5.4
7.5
3
(2)①甲、乙平均成绩一样,甲方差较小,甲发挥更稳定.
②从平均数和中位数相结合看,乙的成绩更好些.
③从平均数和命中9环以上的次数相结合看,说明乙的成绩好些.
④乙的成绩呈上升趋势,乙更有潜力.
题号
一
二
三
四
五
六
总分
得分
座位号
(说明:本卷共有六个大题,23个小题,全卷满分120分,考试时间120分钟.)
选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项,请将正确选项的代号填在题后的括号内)
1.一组数据:0,1,2,3,3,5,5,10的中位数是( )
A. 2.5 B. 3 C. 3.5 D. 5
2.一组数据为-1,0,4,x,6,16,这组数据的中位数为 5,则这组数据众数可能是( )
A. 5 B. 6 C. -1 D. 5.5
3.李东同学参加校团委组织的演讲赛,共21名选手参赛,预赛成绩各不相同,按成绩取前10名的选手参加复赛,李东在知道自己成绩的情况下,要判断自己能否进入复赛,还需要知道这21名选手成绩的( )
A. 平均数 B. 方差 C. 众数 D. 中位数
4.如果一组数据x1,x2,…,xn的方差是4,则另一组数据x1+3,x2+3,…,xn+3的方差是( )
A. 4 B. 7 C. 8 D. 19
5.如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
A. 中位数是6.5 B. 平均数高于众数
C. 极差为3 D. 平均每周锻炼超过6小时的人占总数的一半
6.某校2015年九年级(1)班全体学生初中毕业体育考试的成绩统计如下表所示:
成绩(分)
35
39
42
44
45
48
50
人数(人)
2
5
6
6
8
7
6
根据上表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学 B. 该班学生这次考试成绩的众数是45分
C. 该班学生这次考试成绩的中位数是45分 D. 该班学生这次考试成绩的平均数是45分
二、填空题(本大题共6小题,每小题3分,共18分)
某大学自主招生考试只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算。已知孔明数学得分为95分,综合得分为93分,那么孔明物理得分是________分。
8.一组数据a,b,c,d,e的平均数是7,则另一组数据a+2,b+2,c+2,d+2,e+2的平均数为_______.
9.某校运动会前夕,要选择256名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的________(填“平均数”、“中位数”或“众数”).
10.某校篮球队 21 名同学的身高如下表:
则该校篮球队 21 名同学身高的中位数是________cm.
11.在演唱比赛中,8位评委给一名歌手的演唱打分如下:9.3,9.5,9.9,9.4,9.3,8.9,9.2,9.6,若去掉一个最高分和一个最低分后的平均分为最后得分,则这名歌手的最后得分约为_________.(结果保留一位小数)
12.已知点(x1,y1)(x2,y2)(x3,y3)都在函数y=3x-7的图像上,若数据x1、x2、x3的方差为3, 则另一组数据y1、y2、y3的方差为________.
三、(本大题共5小题,每小题6分,共30分)
13.乐乐是一名健步走运动的爱好者,她用手机软件记录了某个月(30 天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
(1)若乐乐这个月平均每天健步走的步数为 1.32 万步,试求她走 1.3 万步和 1.5 万步的天数;
(2)求这组数据中的众数和中位数.
14.某车间为了改变管理松懈的状况,准备采取每天任务定额和超产有奖的措施,从而提高工作效率.下面是该车间15名工人过去一天中各自装配机器的数量(单位:台):
15,6,16,7,15,8,7,13,8,11,8,10,9,10,9.
请回答下列问题:
(1)这组数据的平均数、众数和中位数各是多少(结果精确到0.01台)?
(2)管理者应确定每人标准日产量为多少台比较合适?
15.一家面临倒闭的企业在“调整产业结构,转变经营机制”的改革后,扭亏为盈. 下表是该企业2015年8~12月、2016年第一季度的月利润统计表:
根据以上信息,解答下列问题:
(1)2015年8月至2016年1月该企业利润的月平均利润为____万元,月利润的中位数为_____万元;
已知该企业2016年2、3月份的月利润的平均增长率相同,求这个平均增长率和2月份的月利润.
16.王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
17.学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手
表达能力
阅读理解
综合素质
汉字听写
甲
85
78
85
73
乙
73
80
82
83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
四、(本大题共3小题,每小题8分,共24分)
18.为了方便居民低碳出行,2016年10月1日起,聊城市公共自行车租赁系统(一期)试运行,越来越多的居民选择公共自行车作为出行的交通工具,市区某中学课外兴趣小组为了了解某小区居民出行方式的变化情况,随机抽取了该小区部分居民进行调查,并绘制了如图的条形统计图和扇形统计图(部分信息未给出)
请根据上面的统计图,解答下列问题:
(1)被调查的总人数是 ______ 人;
(2)公共自行车租赁系统运行后,被调查居民选择自行车作为出行方式的百分比提高了多少?
(3)如果该小区共有居民2000人,公共自行车租赁系统运行后估计选择自行车作为出行方式的有多少人?
19.本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
(1)本次选取参加测试的学生人数是______;
(2)学生“信息素养”得分的中位数落在______ ;
(3)若把每组中各个分数用这组数据的中间值代替(如30﹣40分的中间值为35分),则参加测试的学生的平均分为多少分?
20.某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款 5 元,初中生每人捐款 10 元,高中生每人捐款 15 元,大学生每人捐款 20 元.问平均每人捐款是多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)——记录下来,则在这组数据中,众数是多少?
五、(本大题共2小题,每小题9分,共18分)
21.某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数的值为_______,所抽查的学生人数为______;
(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
22.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
(1)在图①中,“80分”所在扇形的圆心角度数为 ;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
六、(本大题共12分)
23.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
1
乙
5.4
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
(五)
一.1.B 2.B 3.D 4.A 5.B 6.D
二.7. 90分8. 9 9. 众数10.187 11.9.4 12. 27
三.13.(1)6天,4天;(2)众数是1.4万步,中位数为1.3万步
【解析】(1)设乐乐有天每天走1.3万步,有天每天走1.5万步,
则 解得
即乐乐有6天每天走1.3万步,有4天每天走1.5万步.
(2)众数是1.4万步,中位数为1.3万步.
14.(1)平均数是10.13台;中位数是9台;众数是8台(2)管理者应确定每人标准日产量为9台比较合适
试题解析:(1)平均数是 (15+6+16+7+15+8+7+13+8+11+8+10+9+10+9)≈10.13(台);中位数是9台;众数是8台.
(2)管理者应确定每人标准日产量为9台比较合适.
因为:若规定8台,则大多数工人不需要努力就可以完成任务,不利于促进生产;
若规定10台为标准日产量,则多数工人不可能超过,甚至还完不成定额,回挫伤生产积极性,比较合理的生产定额应该确定在恰好能使多数人有超过的能力,因此取中位数9台比较合适。
15.(1)45,45;(2)2月份利润为60万元.
试题解析:(1)2015年8月至2016年1月该企业利润的月平均利润为 45 万元,月利润的中位数为 45 万元;
(2)设该企业月平均增长率为x,则
50(1+x)2=72
x=0.2或-2.2(舍去)
∴2月份利润:50(1+0.2)=60万元
16.(1)7840千克;(2)乙山上的杨梅产量较稳定.
试题解析:(1)甲山上4棵树的产量分别为:50千克、36千克、40千克、34千克,
所以甲山产量的样本平均数为: 千克;
乙山上4棵树的产量分别为:36千克、40千克、48千克、36千克,
所以乙山产量的样本平均数为千克.
总产量为40×100×98%×2=7840(千克)
答:甲、乙两片山上杨梅产量数样本的平均数分别为:40kg,40kg;
(2)由题意,得
S甲2=(千克2);
S乙2=(千克2)
∵38>24
∴S2甲>S2乙
∴乙山上的杨梅产量较稳定.
17.甲;乙
解:(1)=(73+80+82+83)÷4=79.5,
∵80.25>79.5,
∴应选派甲;
(2)=(85×2+78×1+85×3+73×4)÷(2+1+3+4)=79.5,
=(73×2+80×1+82×3+83×4)÷(2+1+3+4)=80.4,
∵79.5<80.4,
∴应选派乙.
四.18.(1)50;(2)20%;(3)1000人
试题解析:(1)由条形图可知,被调查的总人数是10+15+25=50人,
(2)共自行车租公赁系统运行前,居民选择自行车作为出行方式的百分比为:15÷50=30%,
公共自行车租赁系统运行后,居民选择自行车作为出行方式的百分比为:100%-36%-14%=50%,
50%-30%=20%,
答:公共自行车租赁系统运行后,被调查居民选择自行车作为出行方式的百分比提高了20%;
(3)公共自行车租赁系统运行后估计选择自行车作为出行方式的有:2000×50%=1000人.
19.(1)50人;
(2)70分~80分组;
(3)参加测试的学生的平均分为73.8分.
试题解析:(1)8+10+16+12+4=50;
(2)学生“信息素养”得分的中位数是70分~80分组;
(3)(8×55+10×65+16×75+12×85+4×95)÷50=3690÷50=73.8(分)
答:参加测试的学生的平均分为73.8分。
20.(1)80 人;(2)11.5 元; (3)10 元.
试题解析:解:(1)参加这次夏令营活动的初中生共有200×(1-10%-20%-30%)=80人; (2)小学生、高中生和大学生的人数为200×20%=40,200×30%=60,200×10%=20, 所以平均每人捐款==11.5(元); (3)因为初中生最多,所以众数为10(元).
五.21.(1)45% ,60人;(2)补全图见解析;(3)7.2小时;(4)780人.
【解析】(1)45% ,60人;
(2)平均睡眠时间为8小时的人数为60×30%=18人,补全图例如下
(3)这部分学生的平均睡眠时间的平均数为7.2小时;
(4)∵抽取的60名学生中,睡眠时间在8小时以下的有12+27=39人,
∴1200名学生中睡眠不足的有×1200=780人.
22.(1)54°;(2)补图见解析;(3)85分;(4)甲班20同名同学的成绩比较整齐.
试题解析:(1)6÷30%=20,
3÷20=15%,
360°×15%=54°;
(2)20-6-3-6=5,统计图补充如下:
(3)20-1-7-8=4,
=85;
(4)∵S甲2<S乙2,
∴甲班20同名同学的成绩比较整齐.
六.23.【解析】(1)根据平均数、中位数、方差的求法.
(2)①平均数相同的情况下,比较方差看谁更为稳定.
②乙的中位数比甲大,说明乙中间水平比甲高.
③乙命中9环以上的次数是3次,而甲只有一次.
④从折线统计图上看,乙在不断地上升,并且得到较高环次数也较多,说明乙具备潜力.
(1)如表
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
7
1
乙
7
5.4
7.5
3
(2)①甲、乙平均成绩一样,甲方差较小,甲发挥更稳定.
②从平均数和中位数相结合看,乙的成绩更好些.
③从平均数和命中9环以上的次数相结合看,说明乙的成绩好些.
④乙的成绩呈上升趋势,乙更有潜力.
