华东师大版八年级下《第17章函数及其图象》单元测试(A)含答案
文档属性
| 名称 | 华东师大版八年级下《第17章函数及其图象》单元测试(A)含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 114.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-26 00:00:00 | ||
图片预览

文档简介
《第17章函数及其图象》单元测试A
一、选择(每小题3分,共24分)
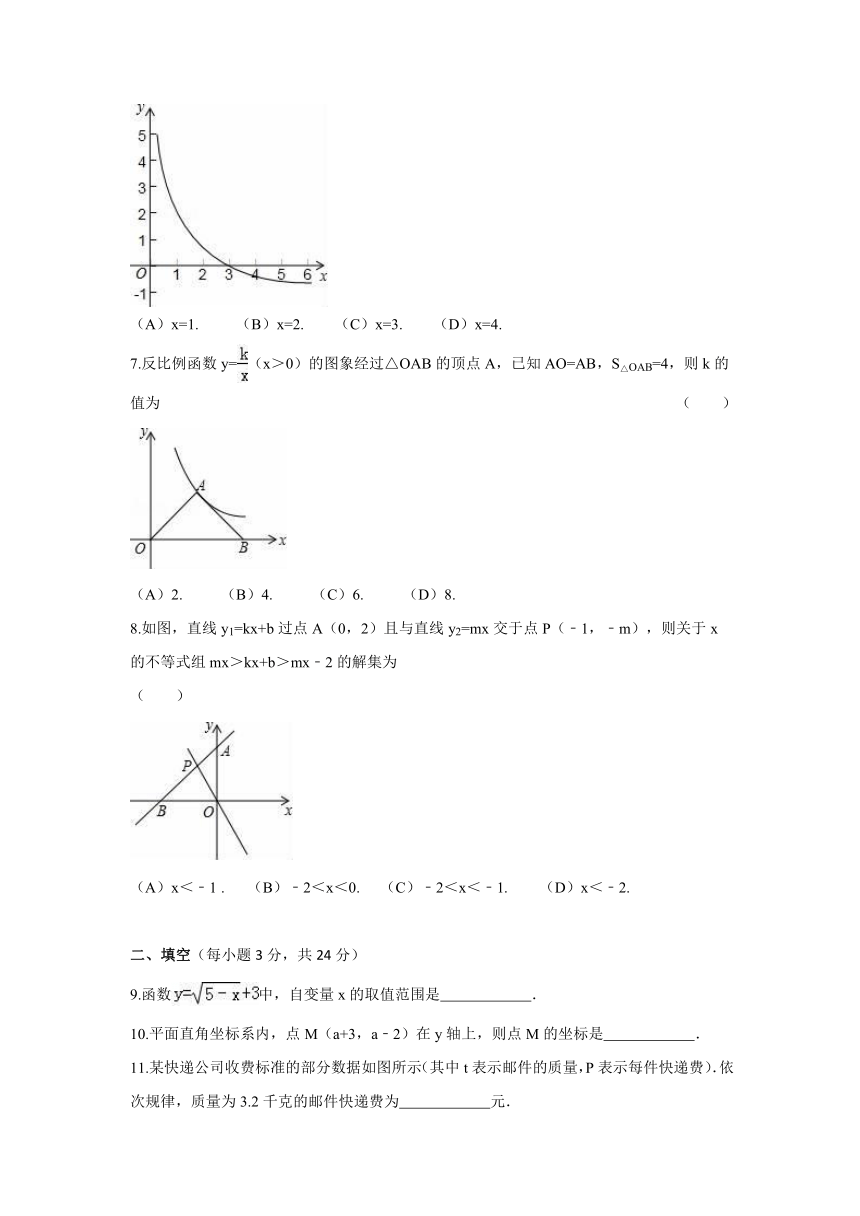
1.下列各点中,在第二象限的点是 ( )
(A)(5,3). (B)(5,﹣3). (C)(﹣5,3). (D)(﹣5,﹣3).
2.根据下列所示的程序计算y的值,若输入的x值为﹣3,则输出的结果为 ( )
(A)5. (B)﹣1. (C)﹣5. (D)1.
3.如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是 ( )
(A). (B). (C). (D).
4.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是 ( )
(A). (B). (C). (D).
5.下列描述一次函数y=﹣2x+5的图象及性质错误的是 ( )
(A)y随x的增大而减小. (B)直线经过第一、二、四象限.
(C)当x>0时y<5. (D)直线与x轴交点坐标是(0,5).
6.小颖画了一个函数y=﹣1的图象如图,那么关于x的分式方程=1的解是 ( )
(A)x=1. (B)x=2. (C)x=3. (D)x=4.
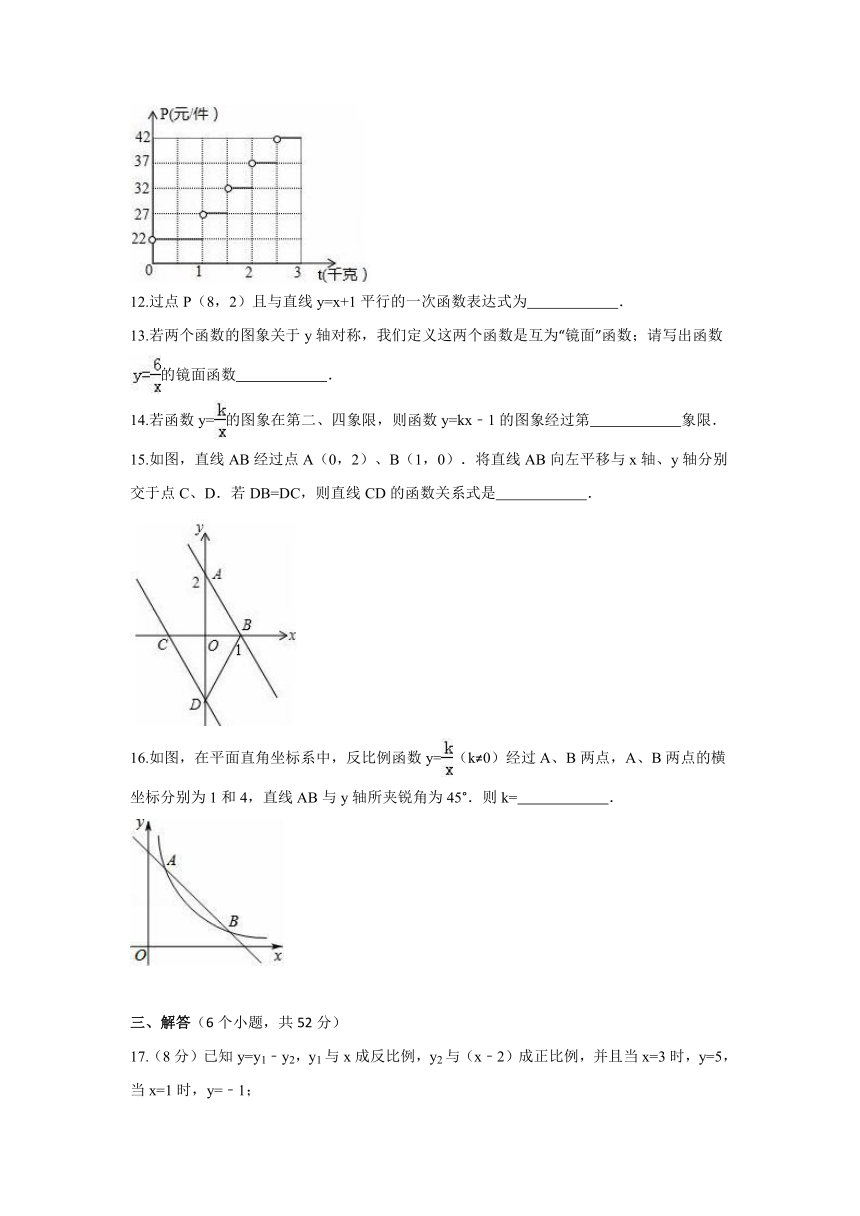
7.反比例函数y=(x>0)的图象经过△OAB的顶点A,已知AO=AB,S△OAB=4,则k的值为 ( )
(A)2. (B)4. (C)6. (D)8.
8.如图,直线y1=kx+b过点A(0,2)且与直线y2=mx交于点P(﹣1,﹣m),则关于x的不等式组mx>kx+b>mx﹣2的解集为 ( )
(A)x<﹣1 . (B)﹣2<x<0. (C)﹣2<x<﹣1. (D)x<﹣2.
二、填空(每小题3分,共24分)
9.函数中,自变量x的取值范围是 .
10.平面直角坐标系内,点M(a+3,a﹣2)在y轴上,则点M的坐标是 .
11.某快递公司收费标准的部分数据如图所示(其中t表示邮件的质量,P表示每件快递费).依次规律,质量为3.2千克的邮件快递费为 元.
12.过点P(8,2)且与直线y=x+1平行的一次函数表达式为 .
13.若两个函数的图象关于y轴对称,我们定义这两个函数是互为“镜面”函数;请写出函数的镜面函数 .
14.若函数y=的图象在第二、四象限,则函数y=kx﹣1的图象经过第 象限.
15.如图,直线AB经过点A(0,2)、B(1,0).将直线AB向左平移与x轴、y轴分别交于点C、D.若DB=DC,则直线CD的函数关系式是 .
16.如图,在平面直角坐标系中,反比例函数y=(k≠0)经过A、B两点,A、B两点的横坐标分别为1和4,直线AB与y轴所夹锐角为45°.则k= .
三、解答(6个小题,共52分)
17.(8分)已知y=y1﹣y2,y1与x成反比例,y2与(x﹣2)成正比例,并且当x=3时,y=5,当x=1时,y=﹣1;
(1)求y与x之间的函数关系式.
(2)当x=时,求y的值.
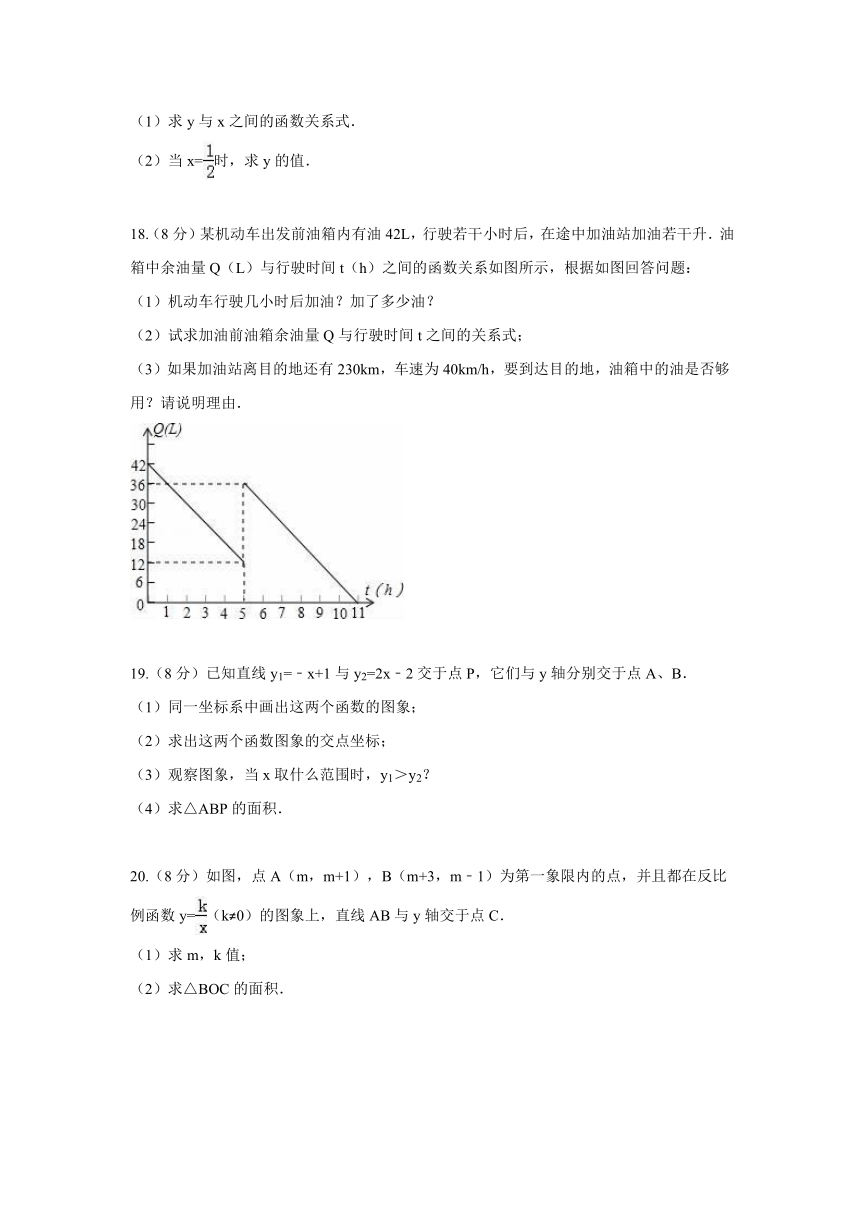
18.(8分)某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
(1)机动车行驶几小时后加油?加了多少油?
(2)试求加油前油箱余油量Q与行驶时间t之间的关系式;
(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
19.(8分)已知直线y1=﹣x+1与y2=2x﹣2交于点P,它们与y轴分别交于点A、B.
(1)同一坐标系中画出这两个函数的图象;
(2)求出这两个函数图象的交点坐标;
(3)观察图象,当x取什么范围时,y1>y2?
(4)求△ABP的面积.
20.(8分)如图,点A(m,m+1),B(m+3,m﹣1)为第一象限内的点,并且都在反比例函数y=(k≠0)的图象上,直线AB与y轴交于点C.
(1)求m,k值;
(2)求△BOC的面积.
21.(10分)如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=与直线y2=﹣x+b交于A,D两点,直线y2=﹣x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.
(1)求m和b的值;
(2)求y1>y2时x的取值范围.
22.(10分)虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧.为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨)
单价(元/吨)
不大于10吨部分
1.5
大于10吨不大于m吨部分(20≤m≤50)
2
大于m吨部分
3
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
参考答案
一、1. C 2.B 3.D 4.B 5.D 6.C 7.B 8.C
二、9. x≤5 10.(0,﹣5) 11.47 12.y=x﹣6 13.y=﹣ 14.二、三、四 15.y=﹣2x﹣2 16.4
三、17. 解:(1)解:设y1=,y2=b(x﹣2),
∵y=y1﹣y2,
∴y=﹣b(x﹣2),
把x=3,y=5和x=1,y=﹣1代入得:,
解得:a=3,b=﹣4,
∴y与x之间的函数关系式是:y=+4x﹣8;
(2)把x=代入y=+4x﹣8中得:y=6+2﹣8=0.
18.解:(1)由横坐标看出,5小时后加油,由纵坐标看出,加了36﹣12=24(L)油
(2)设表达式为Q=kt+b,将(0,42),(5,12)代入函数表达式,得
,解得.
∴函数表达式为Q=42﹣6t
(3)够用,理由如下:
36L的油还可以行驶6小时,
∵车速为40km/h,
∴36L的油可以行驶240千米,
240>230.
故油够用.
19.解:(1)∵当x=0时,y1=1.y1=0时,x=1.
∴直线y1=﹣x+1经过点(0,1),(1,0).
同理,y2=2x﹣2经过点(0,﹣2),(1,0).
则其图象如图所示:
;
(2)由(1)中的两直线图象知,这两个函数图象的交点坐标是(1,0);
(3)由(1)中的两直线图象知,当<1时,y1>y2;
(4)∵A(0,1),P(1,0).B(0,﹣2),
∴AB=3,OP=1,
∴△ABP的面积是: AB?OP=×3×1=.
20.解:(1)∵点A(m,m+1),B(m+3,m﹣1)都在反比例函数y=(k≠0)的图象上,
∴k=m(m+1)=(m+3)(m﹣1),
解得m=3,k=12;
(2)∵m=3,
∴A(3,4),B(6,2).
设直线AB的表达式为y=ax+b,
,解得,
∴直线AB的表达式为y=﹣x+6,
∴C(0,6),
∴△BOC的面积=×6×6=18.
21.解:(1)∵点B在直线y2=﹣x+b上,
∴b=3,
∴y2=﹣x+3,
设A点的坐标为(x,n),∵S△AOB=3,
∴|x|=3,x<0,
∴x=﹣2,n=﹣(﹣2)+3=5,
∴A(﹣2,5),
∵y1=过点A,∴m=(﹣2)×5=﹣10,
所以,m=﹣10,b=3,
(2)∵y2=﹣x+3,易得C点坐标为(3,0),
同(1)可得,D点坐标为(5,﹣2),
由图象可知,当y1>y2时,﹣2<x<0或x>5
22.解:(1)∵18<m,
∴此时前面10吨每吨收1.5元,后面8吨每吨收2元,
10×1.5+(18﹣10)×2=31,
(2)①当x≤10时,y=1.5x,
②当10<x≤m时,y=10×1.5+(x﹣10)×2=2x﹣5,
③当x>m时,y=10×1.5+(m﹣10)×2+(x﹣m)×3=3x﹣m﹣5,
∴
(3)∵10≤x≤50,
∴当用水量为40吨时就有可能是按照第二和第三两种方式收费,
①当40≤m≤50时,此时选择第二种方案,费用=2×40﹣5=75,符合题意,
②当10≤m<40时,此时选择第三种方案,费用=3x﹣m﹣5,
则:70≤3x﹣m﹣5≤90,
∴25≤m≤45,
∴此状况下25≤m<40,
综合①、②可得m的取值范围为:25≤m≤50.
一、选择(每小题3分,共24分)
1.下列各点中,在第二象限的点是 ( )
(A)(5,3). (B)(5,﹣3). (C)(﹣5,3). (D)(﹣5,﹣3).
2.根据下列所示的程序计算y的值,若输入的x值为﹣3,则输出的结果为 ( )
(A)5. (B)﹣1. (C)﹣5. (D)1.
3.如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是 ( )
(A). (B). (C). (D).
4.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是 ( )
(A). (B). (C). (D).
5.下列描述一次函数y=﹣2x+5的图象及性质错误的是 ( )
(A)y随x的增大而减小. (B)直线经过第一、二、四象限.
(C)当x>0时y<5. (D)直线与x轴交点坐标是(0,5).
6.小颖画了一个函数y=﹣1的图象如图,那么关于x的分式方程=1的解是 ( )
(A)x=1. (B)x=2. (C)x=3. (D)x=4.
7.反比例函数y=(x>0)的图象经过△OAB的顶点A,已知AO=AB,S△OAB=4,则k的值为 ( )
(A)2. (B)4. (C)6. (D)8.
8.如图,直线y1=kx+b过点A(0,2)且与直线y2=mx交于点P(﹣1,﹣m),则关于x的不等式组mx>kx+b>mx﹣2的解集为 ( )
(A)x<﹣1 . (B)﹣2<x<0. (C)﹣2<x<﹣1. (D)x<﹣2.
二、填空(每小题3分,共24分)
9.函数中,自变量x的取值范围是 .
10.平面直角坐标系内,点M(a+3,a﹣2)在y轴上,则点M的坐标是 .
11.某快递公司收费标准的部分数据如图所示(其中t表示邮件的质量,P表示每件快递费).依次规律,质量为3.2千克的邮件快递费为 元.
12.过点P(8,2)且与直线y=x+1平行的一次函数表达式为 .
13.若两个函数的图象关于y轴对称,我们定义这两个函数是互为“镜面”函数;请写出函数的镜面函数 .
14.若函数y=的图象在第二、四象限,则函数y=kx﹣1的图象经过第 象限.
15.如图,直线AB经过点A(0,2)、B(1,0).将直线AB向左平移与x轴、y轴分别交于点C、D.若DB=DC,则直线CD的函数关系式是 .
16.如图,在平面直角坐标系中,反比例函数y=(k≠0)经过A、B两点,A、B两点的横坐标分别为1和4,直线AB与y轴所夹锐角为45°.则k= .
三、解答(6个小题,共52分)
17.(8分)已知y=y1﹣y2,y1与x成反比例,y2与(x﹣2)成正比例,并且当x=3时,y=5,当x=1时,y=﹣1;
(1)求y与x之间的函数关系式.
(2)当x=时,求y的值.
18.(8分)某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
(1)机动车行驶几小时后加油?加了多少油?
(2)试求加油前油箱余油量Q与行驶时间t之间的关系式;
(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
19.(8分)已知直线y1=﹣x+1与y2=2x﹣2交于点P,它们与y轴分别交于点A、B.
(1)同一坐标系中画出这两个函数的图象;
(2)求出这两个函数图象的交点坐标;
(3)观察图象,当x取什么范围时,y1>y2?
(4)求△ABP的面积.
20.(8分)如图,点A(m,m+1),B(m+3,m﹣1)为第一象限内的点,并且都在反比例函数y=(k≠0)的图象上,直线AB与y轴交于点C.
(1)求m,k值;
(2)求△BOC的面积.
21.(10分)如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=与直线y2=﹣x+b交于A,D两点,直线y2=﹣x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.
(1)求m和b的值;
(2)求y1>y2时x的取值范围.
22.(10分)虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧.为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨)
单价(元/吨)
不大于10吨部分
1.5
大于10吨不大于m吨部分(20≤m≤50)
2
大于m吨部分
3
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
参考答案
一、1. C 2.B 3.D 4.B 5.D 6.C 7.B 8.C
二、9. x≤5 10.(0,﹣5) 11.47 12.y=x﹣6 13.y=﹣ 14.二、三、四 15.y=﹣2x﹣2 16.4
三、17. 解:(1)解:设y1=,y2=b(x﹣2),
∵y=y1﹣y2,
∴y=﹣b(x﹣2),
把x=3,y=5和x=1,y=﹣1代入得:,
解得:a=3,b=﹣4,
∴y与x之间的函数关系式是:y=+4x﹣8;
(2)把x=代入y=+4x﹣8中得:y=6+2﹣8=0.
18.解:(1)由横坐标看出,5小时后加油,由纵坐标看出,加了36﹣12=24(L)油
(2)设表达式为Q=kt+b,将(0,42),(5,12)代入函数表达式,得
,解得.
∴函数表达式为Q=42﹣6t
(3)够用,理由如下:
36L的油还可以行驶6小时,
∵车速为40km/h,
∴36L的油可以行驶240千米,
240>230.
故油够用.
19.解:(1)∵当x=0时,y1=1.y1=0时,x=1.
∴直线y1=﹣x+1经过点(0,1),(1,0).
同理,y2=2x﹣2经过点(0,﹣2),(1,0).
则其图象如图所示:
;
(2)由(1)中的两直线图象知,这两个函数图象的交点坐标是(1,0);
(3)由(1)中的两直线图象知,当<1时,y1>y2;
(4)∵A(0,1),P(1,0).B(0,﹣2),
∴AB=3,OP=1,
∴△ABP的面积是: AB?OP=×3×1=.
20.解:(1)∵点A(m,m+1),B(m+3,m﹣1)都在反比例函数y=(k≠0)的图象上,
∴k=m(m+1)=(m+3)(m﹣1),
解得m=3,k=12;
(2)∵m=3,
∴A(3,4),B(6,2).
设直线AB的表达式为y=ax+b,
,解得,
∴直线AB的表达式为y=﹣x+6,
∴C(0,6),
∴△BOC的面积=×6×6=18.
21.解:(1)∵点B在直线y2=﹣x+b上,
∴b=3,
∴y2=﹣x+3,
设A点的坐标为(x,n),∵S△AOB=3,
∴|x|=3,x<0,
∴x=﹣2,n=﹣(﹣2)+3=5,
∴A(﹣2,5),
∵y1=过点A,∴m=(﹣2)×5=﹣10,
所以,m=﹣10,b=3,
(2)∵y2=﹣x+3,易得C点坐标为(3,0),
同(1)可得,D点坐标为(5,﹣2),
由图象可知,当y1>y2时,﹣2<x<0或x>5
22.解:(1)∵18<m,
∴此时前面10吨每吨收1.5元,后面8吨每吨收2元,
10×1.5+(18﹣10)×2=31,
(2)①当x≤10时,y=1.5x,
②当10<x≤m时,y=10×1.5+(x﹣10)×2=2x﹣5,
③当x>m时,y=10×1.5+(m﹣10)×2+(x﹣m)×3=3x﹣m﹣5,
∴
(3)∵10≤x≤50,
∴当用水量为40吨时就有可能是按照第二和第三两种方式收费,
①当40≤m≤50时,此时选择第二种方案,费用=2×40﹣5=75,符合题意,
②当10≤m<40时,此时选择第三种方案,费用=3x﹣m﹣5,
则:70≤3x﹣m﹣5≤90,
∴25≤m≤45,
∴此状况下25≤m<40,
综合①、②可得m的取值范围为:25≤m≤50.
