华东师大八年级下册《第17章函数及其图象》单元测试(B)含答案
文档属性
| 名称 | 华东师大八年级下册《第17章函数及其图象》单元测试(B)含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 118.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-26 00:00:00 | ||
图片预览

文档简介
《第17章函数及其图象》单元测试B
一、选择(每小题3分,共24分)
1.如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为 ( )
(A)y=10x. (B)y=25x. (C)y=x. (D)y=x.
2.在平面直角坐标系中,若点P(m,1)在第二象限,则点Q(﹣m,0)在 ( )
(A)x轴正半轴上. (B)y轴正半轴上.
(C)x轴负半轴上. (D)y轴负半轴上.
3.一次函数y=﹣4x﹣5的图象一定不经过 ( )
(A)第一象限. (B)第二象限. (C)第三象限. (D)第四象限.
4.已知点A(﹣2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,则y1与y2的大小关系是 ( )
(A)y1<y2. (B)y1>y2. (C)y1=y2. (D)y1≥y2.
5.星期天,小宇同学骑自行车从家出发到图书馆查阅有关资料,之后就返回了家,如图反映了小宇离家的路程y(米)与骑车时间x(分)的函数关系.从图象得到下列信息,错误的是 ( )
(A)小宇家与图书馆之间路程是3千米.
(B)小宇在图书馆查阅资料花去了42分钟.
(C)小宇从图书馆骑车回家用了10分钟.
(D)小宇从家到图书馆骑车速度比返回的速度慢.
6.已知y﹣1与x成正比,当x=2时,y=9;那么当y=﹣15时,x的值为 ( )
(A)4. (B)﹣4. (C)6. (D)﹣6.
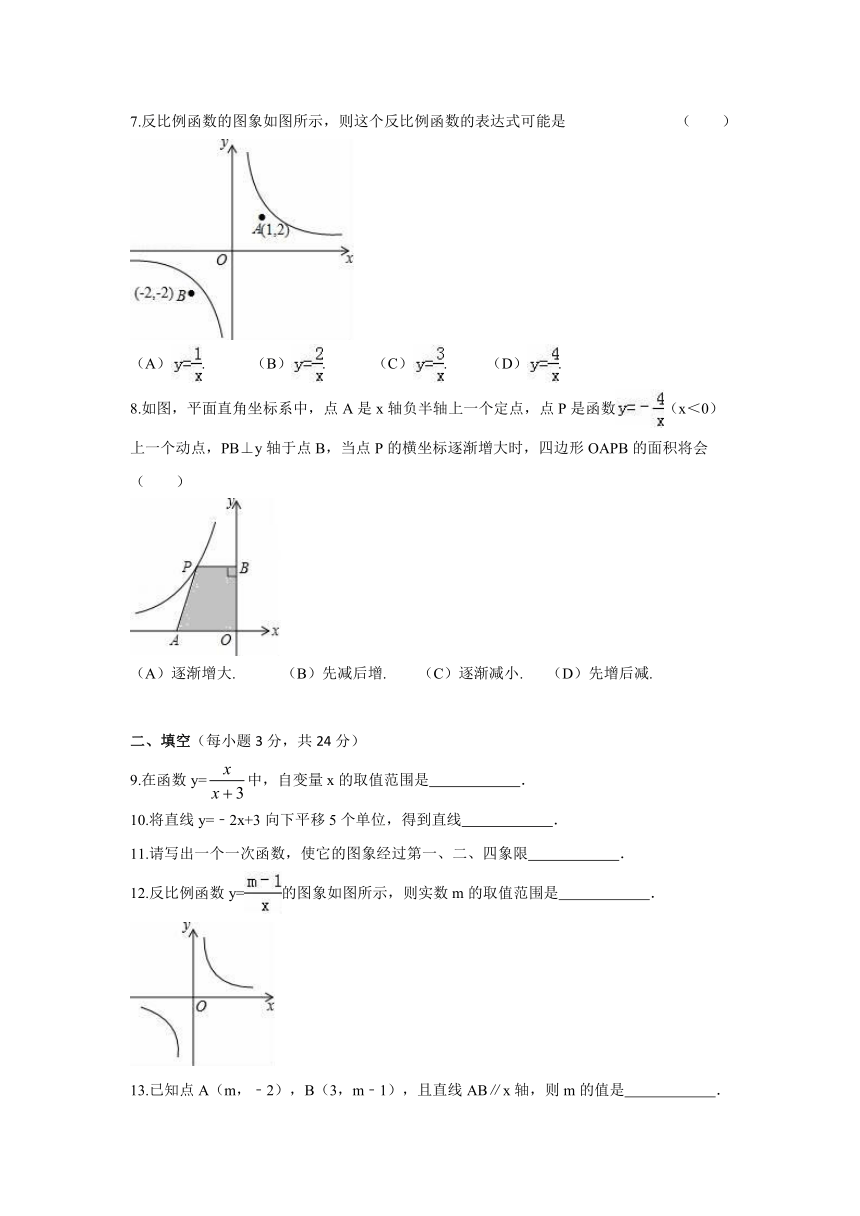
7.反比例函数的图象如图所示,则这个反比例函数的表达式可能是 ( )
(A). (B). (C). (D).
8.如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(A)逐渐增大. (B)先减后增. (C)逐渐减小. (D)先增后减.
二、填空(每小题3分,共24分)
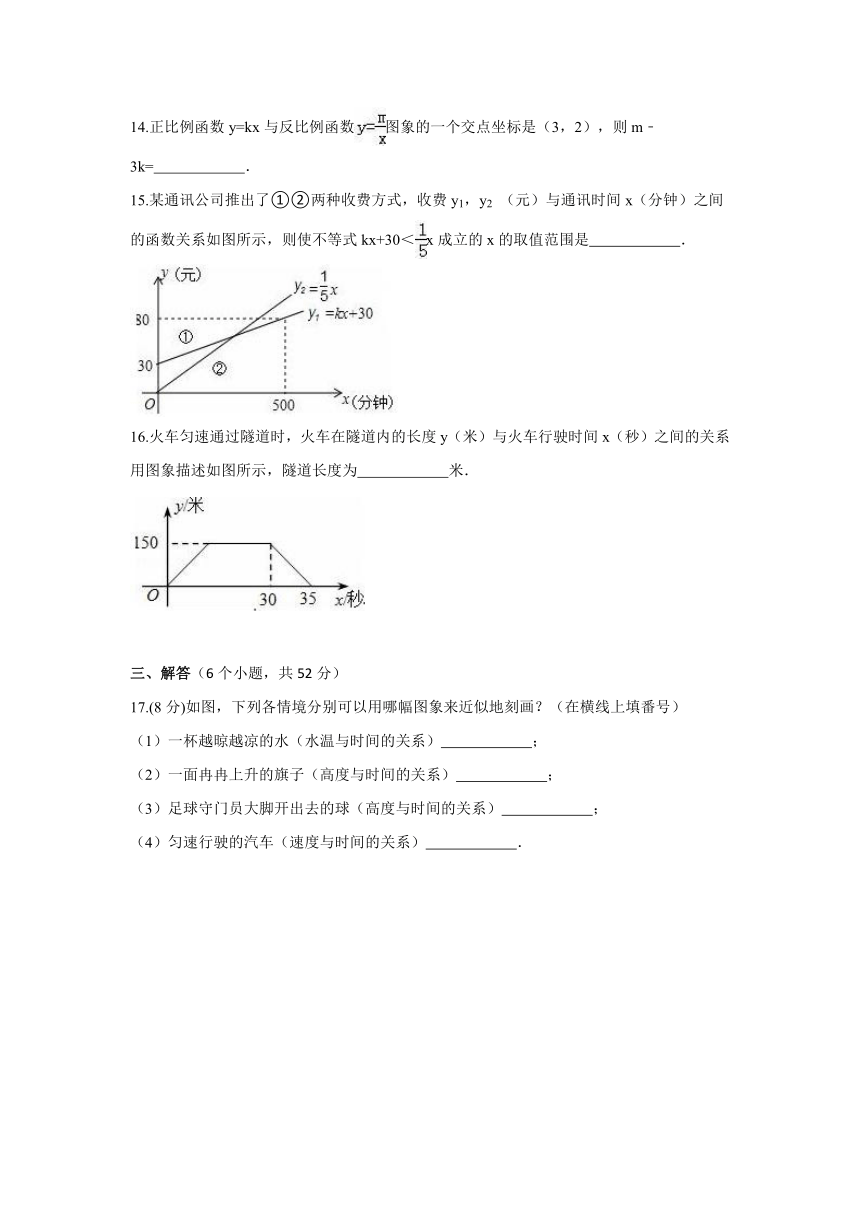
9.在函数y=中,自变量x的取值范围是 .
10.将直线y=﹣2x+3向下平移5个单位,得到直线 .
11.请写出一个一次函数,使它的图象经过第一、二、四象限 .
12.反比例函数y=的图象如图所示,则实数m的取值范围是 .
13.已知点A(m,﹣2),B(3,m﹣1),且直线AB∥x轴,则m的值是 .
14.正比例函数y=kx与反比例函数图象的一个交点坐标是(3,2),则m﹣3k= .
15.某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<x成立的x的取值范围是 .
16.火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,隧道长度为 米.
三、解答(6个小题,共52分)
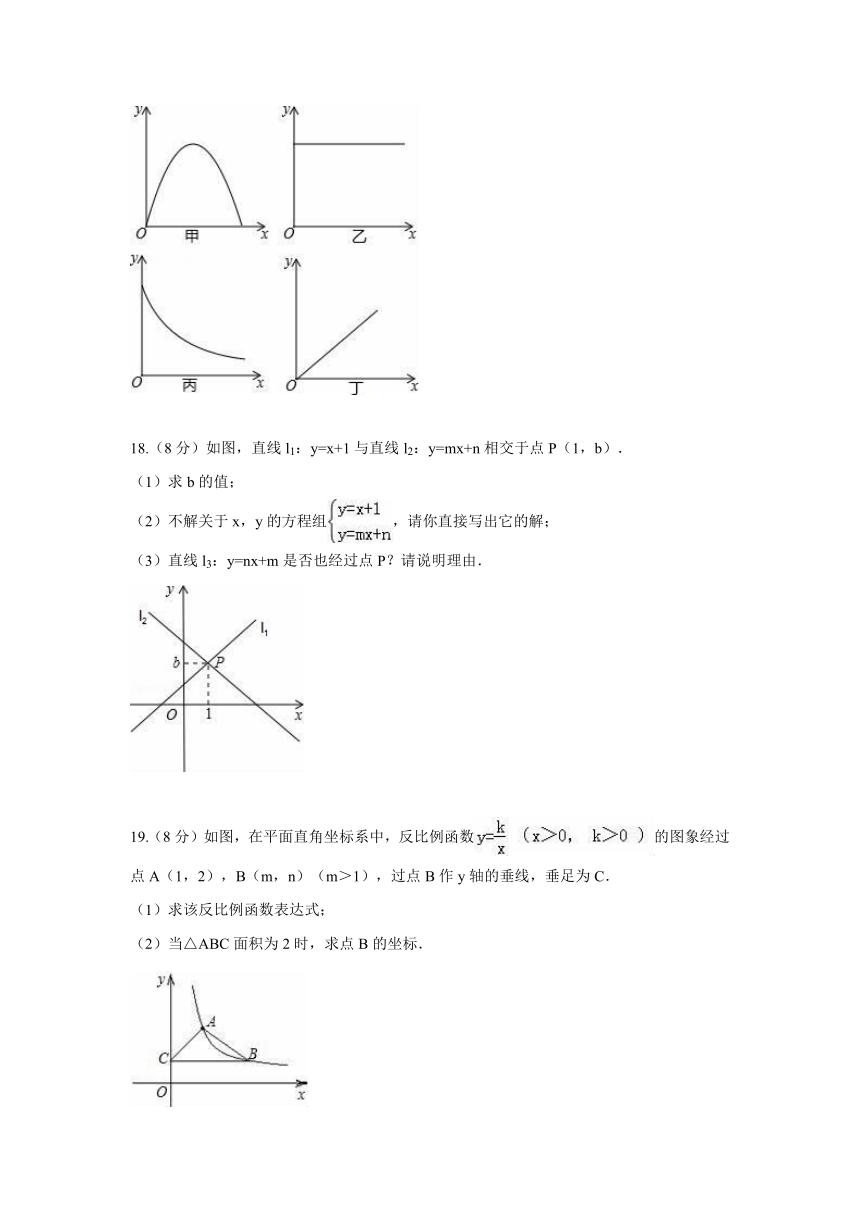
17.(8分)如图,下列各情境分别可以用哪幅图象来近似地刻画?(在横线上填番号)
(1)一杯越晾越凉的水(水温与时间的关系) ;
(2)一面冉冉上升的旗子(高度与时间的关系) ;
(3)足球守门员大脚开出去的球(高度与时间的关系) ;
(4)匀速行驶的汽车(速度与时间的关系) .
18.(8分)如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组,请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
19.(8分)如图,在平面直角坐标系中,反比例函数的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数表达式;
(2)当△ABC面积为2时,求点B的坐标.
20.(8分)保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2018年1月的利润为200万元.设2018年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2018年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
(1)求该化工厂治污期间y与x之间对应的函数关系式.
(2)求5月份的利润及治污改造工程完工后y与x之间对应的函数关系式.
(3)治污改造工程完工后经过几个月,该厂月利润才能达到2014年1月的水平?
21.(10分)在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
22.(10分)如图,已知一次函数y=x+b与反比例函数y=在第二象限的图象交于A(n,)、B(﹣1,2)两点.
(1)求m、n的值;
(2)根据图象回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(3)△AOB的面积是多少?
参考答案
一、1. D 2.A 3.A 4.A 5.B 6.B 7.C 8.A
二、9. x≠-3 10.y=﹣2x﹣2 11.y=﹣x+3(答案不唯一) 12.m>1 13.﹣1 14.4 15.x>300 16.900
三、17. 解:丙,丁,甲,乙.
18.解:(1)∵(1,b)在直线y=x+1上,
∴当x=1时,b=1+1=2.
(2)解是;
(3)直线y=nx+m也经过点P,
∵点P(1,2)在直线y=mx+n上,
∴m+n=2.
把x=1代入y=nx+m,得n+m=2.
∴直线y=nx+m也经过点P.
19.解:(1)反比例函数表达式为:.
(2)∵S△ABC=,
∴m=3,
∴B的坐标为(3,.
20.解:(1)根据图象,反比例函数图象经过(1,200),
设反比例函数为y=,
解得k=200,
∴反比例函数为y=(x≤5),
当x=5时,y=40,
(2)设改造工程完工后函数表达式为y=40+20(x-5)=20x-60,
∴改造工程完工后函数表达式为y=20x﹣60;
(3)当y=200时,20x﹣60=200,
解得x=13.
13﹣5=8
∴经过8个月,该厂利润才能达到200万元;
21.解:(1)设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=kx+b,
由图可知,函数图象过点(2,30),(6,50),
∴,解得,
∴y=5x+20;
(2)由图可知,甲队速度是:60÷6=10(米/时),
设甲队从开始到完工所铺设彩色道砖的长度为z米,
依题意,得=,
解得z=110,
答:甲队从开始到完工所铺设彩色道砖的长度为110米.
22.解:(1)∵反比例函数y=的图象经过点B(﹣1,2),
∴m=﹣1×2=﹣2;
又∵反比例函数y=﹣的图象经过点A(n,),
∴n=﹣2÷=﹣4;
(2)∵一次函数y=x+b与反比例函数y=在第二象限的图象交于A(﹣4,)、B(﹣1,2)两点,
∴当﹣4<x<﹣1时,一次函数大于反比例函数的值;
(3)过A、B分别作AF⊥y轴于F,BE⊥y轴于E,
S△AOB=S梯形ABEF+S△AOF﹣S△BOE
=S梯形ABEF
=×(1+4)×(2﹣)
=.
一、选择(每小题3分,共24分)
1.如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为 ( )
(A)y=10x. (B)y=25x. (C)y=x. (D)y=x.
2.在平面直角坐标系中,若点P(m,1)在第二象限,则点Q(﹣m,0)在 ( )
(A)x轴正半轴上. (B)y轴正半轴上.
(C)x轴负半轴上. (D)y轴负半轴上.
3.一次函数y=﹣4x﹣5的图象一定不经过 ( )
(A)第一象限. (B)第二象限. (C)第三象限. (D)第四象限.
4.已知点A(﹣2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,则y1与y2的大小关系是 ( )
(A)y1<y2. (B)y1>y2. (C)y1=y2. (D)y1≥y2.
5.星期天,小宇同学骑自行车从家出发到图书馆查阅有关资料,之后就返回了家,如图反映了小宇离家的路程y(米)与骑车时间x(分)的函数关系.从图象得到下列信息,错误的是 ( )
(A)小宇家与图书馆之间路程是3千米.
(B)小宇在图书馆查阅资料花去了42分钟.
(C)小宇从图书馆骑车回家用了10分钟.
(D)小宇从家到图书馆骑车速度比返回的速度慢.
6.已知y﹣1与x成正比,当x=2时,y=9;那么当y=﹣15时,x的值为 ( )
(A)4. (B)﹣4. (C)6. (D)﹣6.
7.反比例函数的图象如图所示,则这个反比例函数的表达式可能是 ( )
(A). (B). (C). (D).
8.如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(A)逐渐增大. (B)先减后增. (C)逐渐减小. (D)先增后减.
二、填空(每小题3分,共24分)
9.在函数y=中,自变量x的取值范围是 .
10.将直线y=﹣2x+3向下平移5个单位,得到直线 .
11.请写出一个一次函数,使它的图象经过第一、二、四象限 .
12.反比例函数y=的图象如图所示,则实数m的取值范围是 .
13.已知点A(m,﹣2),B(3,m﹣1),且直线AB∥x轴,则m的值是 .
14.正比例函数y=kx与反比例函数图象的一个交点坐标是(3,2),则m﹣3k= .
15.某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<x成立的x的取值范围是 .
16.火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,隧道长度为 米.
三、解答(6个小题,共52分)
17.(8分)如图,下列各情境分别可以用哪幅图象来近似地刻画?(在横线上填番号)
(1)一杯越晾越凉的水(水温与时间的关系) ;
(2)一面冉冉上升的旗子(高度与时间的关系) ;
(3)足球守门员大脚开出去的球(高度与时间的关系) ;
(4)匀速行驶的汽车(速度与时间的关系) .
18.(8分)如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组,请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
19.(8分)如图,在平面直角坐标系中,反比例函数的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数表达式;
(2)当△ABC面积为2时,求点B的坐标.
20.(8分)保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2018年1月的利润为200万元.设2018年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2018年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
(1)求该化工厂治污期间y与x之间对应的函数关系式.
(2)求5月份的利润及治污改造工程完工后y与x之间对应的函数关系式.
(3)治污改造工程完工后经过几个月,该厂月利润才能达到2014年1月的水平?
21.(10分)在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
22.(10分)如图,已知一次函数y=x+b与反比例函数y=在第二象限的图象交于A(n,)、B(﹣1,2)两点.
(1)求m、n的值;
(2)根据图象回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(3)△AOB的面积是多少?
参考答案
一、1. D 2.A 3.A 4.A 5.B 6.B 7.C 8.A
二、9. x≠-3 10.y=﹣2x﹣2 11.y=﹣x+3(答案不唯一) 12.m>1 13.﹣1 14.4 15.x>300 16.900
三、17. 解:丙,丁,甲,乙.
18.解:(1)∵(1,b)在直线y=x+1上,
∴当x=1时,b=1+1=2.
(2)解是;
(3)直线y=nx+m也经过点P,
∵点P(1,2)在直线y=mx+n上,
∴m+n=2.
把x=1代入y=nx+m,得n+m=2.
∴直线y=nx+m也经过点P.
19.解:(1)反比例函数表达式为:.
(2)∵S△ABC=,
∴m=3,
∴B的坐标为(3,.
20.解:(1)根据图象,反比例函数图象经过(1,200),
设反比例函数为y=,
解得k=200,
∴反比例函数为y=(x≤5),
当x=5时,y=40,
(2)设改造工程完工后函数表达式为y=40+20(x-5)=20x-60,
∴改造工程完工后函数表达式为y=20x﹣60;
(3)当y=200时,20x﹣60=200,
解得x=13.
13﹣5=8
∴经过8个月,该厂利润才能达到200万元;
21.解:(1)设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=kx+b,
由图可知,函数图象过点(2,30),(6,50),
∴,解得,
∴y=5x+20;
(2)由图可知,甲队速度是:60÷6=10(米/时),
设甲队从开始到完工所铺设彩色道砖的长度为z米,
依题意,得=,
解得z=110,
答:甲队从开始到完工所铺设彩色道砖的长度为110米.
22.解:(1)∵反比例函数y=的图象经过点B(﹣1,2),
∴m=﹣1×2=﹣2;
又∵反比例函数y=﹣的图象经过点A(n,),
∴n=﹣2÷=﹣4;
(2)∵一次函数y=x+b与反比例函数y=在第二象限的图象交于A(﹣4,)、B(﹣1,2)两点,
∴当﹣4<x<﹣1时,一次函数大于反比例函数的值;
(3)过A、B分别作AF⊥y轴于F,BE⊥y轴于E,
S△AOB=S梯形ABEF+S△AOF﹣S△BOE
=S梯形ABEF
=×(1+4)×(2﹣)
=.
