江苏省兴化市芙蓉外国语实验学校2018~2019学年第二学期七年级数学第7章 平面图形的认识(二)第一周周测试题
文档属性
| 名称 | 江苏省兴化市芙蓉外国语实验学校2018~2019学年第二学期七年级数学第7章 平面图形的认识(二)第一周周测试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-26 00:00:00 | ||
图片预览


文档简介
芙蓉外国语实验学校2018~2019学年第二学期七年级
第一周数学周测
一、选择题(每小题3分,共18分)
1.下列图形中,不能通过其中一个四边形平移得到的是( )
A B C D
2.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
第2题图 第3题图 第4题图
3.如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=65°,则∠2的度数为( )
A.20° B.25° C.30° D.35°
4.如果将一副三角板按如图方式叠放,那么∠1等于( )
A.120° B.105° C.60° D.45°
5.下列长度的三根木棒首尾相接,不能做成三角形的框架的是( )
A.5cm,7cm,10cm B.7cm,10cm,13cm
C.5cm,7cm,13cm D.5cm,10cm,13cm
6.如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为( )
A.15° B.20° C.25° D.30°
第6题图 第8题图 第10题图
二、填空题(每题3分,共30分)
7.若一个等腰三角形的两边长分别为3和6,则这个等腰三角形的周长是 .
8.在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理 .
9.从3cm、5cm、7cm、9cm的四根小棒中任取三根,能围成 个三角形.
10.如图,它是由6个面积为1的小正方形组成的长方形,点A、B、C、D、E、F是小正方形的顶点,以这六个点中的任意三点为顶点,组成面积是1的三角形的个数是 .
11.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数为 .
第11题图 第13题图 第14题图 第15题图
12.七边形的内角和是 .
13.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于 °.
14.如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=35°,那么∠2= 度.
15.如图,是一副形似“秋蝉”的图案,其实线部分是由正方形、正五边形和正六边形叠放在一起形成的,则图中∠MON的度数为 .
16.当三角形中一个内角β是另一个内角α的时,我们称此三角形为“希望三角形”,其中角α称为“希望角”.如果一个“希望三角形”中有一个内角为54°,那么这个“希望三角形”的“希望角”度数为 .
三、解答题(共102分)
17.如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°.
(1)求∠C的度数;
(2)求∠BED的度数.
18.如图,已知∠A=∠C,∠E=∠F.试说明AB∥CD.
19.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=110°,求∠ACB的度数.
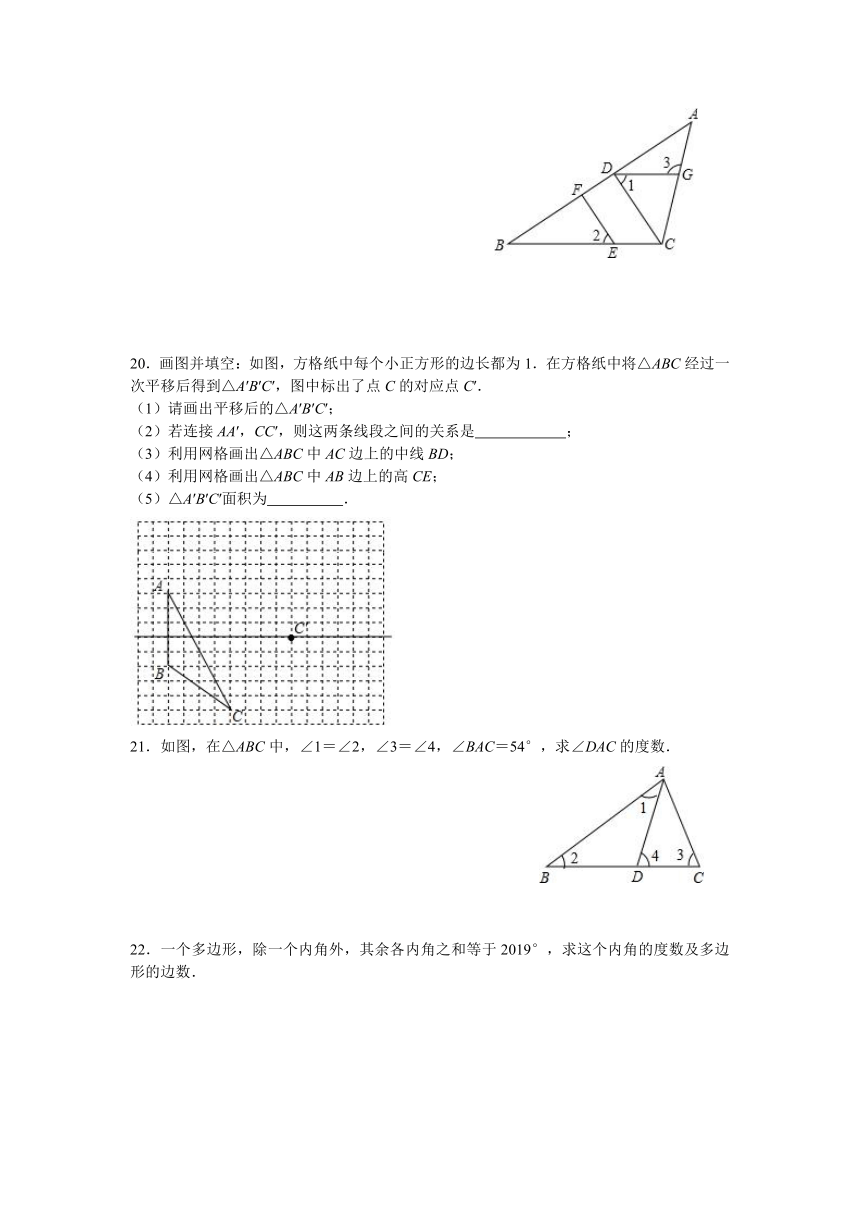
20.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
(1)请画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两条线段之间的关系是 ;
(3)利用网格画出△ABC中AC边上的中线BD;
(4)利用网格画出△ABC中AB边上的高CE;
(5)△A′B′C′面积为 .
21.如图,在△ABC中,∠1=∠2,∠3=∠4,∠BAC=54°,求∠DAC的度数.
22.一个多边形,除一个内角外,其余各内角之和等于2019°,求这个内角的度数及多边形的边数.
23.如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.
24.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案
一、选择题
题号 1 2 3 4 5 6
答案 C A B B C B
二、填空题
7.15
8.三角形的内角和是180°
9.3
10.10
11.20°
12.900°
13.230
14.110
15.33°
16.54°或108°或84°
三、解答题
17.解:(1)∵∠BDC=∠ABD+∠A,
∴∠ABD=∠BDC-∠A=15°.
∵BD平分∠ABC,
∴∠ABC=2∠ABD=30°.
∵∠A+∠ABC+∠C=180°,
∴∠C=180°-∠A-∠ABC=105°.
(2)∵DE∥BC,
∴∠AED=∠ABC=30°.
∵∠BED+∠AED=180°,
∴∠BED=180°-∠AED=150°.
18.证明:∵∠E=∠F,
∴AE∥CF,
∴∠A=∠ABF,
∵∠A=∠C,
∴∠ABF=∠C,
∴AB∥CD.
19.解:(1)CD∥EF.
∵CD⊥AB,EF⊥AB,
∴∠BFE=∠BDC=90°,
∴CD∥EF;
(2)由(1)可知CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC,
∴∠ACB=∠3,
∴∠3=110°,
∴∠ACB=110°.
20.解:(1)如图所示:△A′B′C′,即为所求;
(2)AA′与CC′,平行且相等;
(3)如图所示:BD,即为所求;
(4)如图所示:CE,即为所求;
(5)△A′B′C′面积为:×4×5=10.
故答案为:10.
21.解:∵∠1=∠2,∠3=∠4,
∴∠4=2∠1=2∠2=∠3
∴∠2+∠3=3∠2=126°
∴∠2=∠1=42°
∴∠DAC=54°-42°=12°.
22.解:∵2019°÷180°=11,
∴这个多边形的内角和为180°×12=2160°,
∴这个内角的度数是:2160°-2019°=141°
设这个多边形的边数是n,由题意得:(n-2)×180°=2160°
解得:n=14
答:这个内角的度数为141°,多边形的边数为14.
23.解:AE∥CF.
理由如下:∵∠B=∠D=90°,
∴∠BAD+∠BCD=360°-90°×2=180°,
∵AE、CF分别平分∠BAD和∠BCD,
∴∠1=∠BAD,∠2=∠BCD,
∴∠1+∠2=(∠BAD+∠BCD)=×180°=90°,
∵∠B=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∴AE∥CF.
24.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°-(∠ABC+∠ACB)=180°-×100°=130°
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)=(360°-∠ABC-∠ACB)
=(180°+∠A)
=90°+∠A
∴∠Q=180°-(∠QBC+∠QCB)=180°-(90°+∠A )=90°-∠A;
(3)延长BC到F,如图所示
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ=∠ABC+∠MBC=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°-∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°-∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
2019.2.22
第一周数学周测
一、选择题(每小题3分,共18分)
1.下列图形中,不能通过其中一个四边形平移得到的是( )
A B C D
2.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
第2题图 第3题图 第4题图
3.如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=65°,则∠2的度数为( )
A.20° B.25° C.30° D.35°
4.如果将一副三角板按如图方式叠放,那么∠1等于( )
A.120° B.105° C.60° D.45°
5.下列长度的三根木棒首尾相接,不能做成三角形的框架的是( )
A.5cm,7cm,10cm B.7cm,10cm,13cm
C.5cm,7cm,13cm D.5cm,10cm,13cm
6.如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为( )
A.15° B.20° C.25° D.30°
第6题图 第8题图 第10题图
二、填空题(每题3分,共30分)
7.若一个等腰三角形的两边长分别为3和6,则这个等腰三角形的周长是 .
8.在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理 .
9.从3cm、5cm、7cm、9cm的四根小棒中任取三根,能围成 个三角形.
10.如图,它是由6个面积为1的小正方形组成的长方形,点A、B、C、D、E、F是小正方形的顶点,以这六个点中的任意三点为顶点,组成面积是1的三角形的个数是 .
11.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数为 .
第11题图 第13题图 第14题图 第15题图
12.七边形的内角和是 .
13.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于 °.
14.如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=35°,那么∠2= 度.
15.如图,是一副形似“秋蝉”的图案,其实线部分是由正方形、正五边形和正六边形叠放在一起形成的,则图中∠MON的度数为 .
16.当三角形中一个内角β是另一个内角α的时,我们称此三角形为“希望三角形”,其中角α称为“希望角”.如果一个“希望三角形”中有一个内角为54°,那么这个“希望三角形”的“希望角”度数为 .
三、解答题(共102分)
17.如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°.
(1)求∠C的度数;
(2)求∠BED的度数.
18.如图,已知∠A=∠C,∠E=∠F.试说明AB∥CD.
19.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=110°,求∠ACB的度数.
20.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
(1)请画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两条线段之间的关系是 ;
(3)利用网格画出△ABC中AC边上的中线BD;
(4)利用网格画出△ABC中AB边上的高CE;
(5)△A′B′C′面积为 .
21.如图,在△ABC中,∠1=∠2,∠3=∠4,∠BAC=54°,求∠DAC的度数.
22.一个多边形,除一个内角外,其余各内角之和等于2019°,求这个内角的度数及多边形的边数.
23.如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.
24.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案
一、选择题
题号 1 2 3 4 5 6
答案 C A B B C B
二、填空题
7.15
8.三角形的内角和是180°
9.3
10.10
11.20°
12.900°
13.230
14.110
15.33°
16.54°或108°或84°
三、解答题
17.解:(1)∵∠BDC=∠ABD+∠A,
∴∠ABD=∠BDC-∠A=15°.
∵BD平分∠ABC,
∴∠ABC=2∠ABD=30°.
∵∠A+∠ABC+∠C=180°,
∴∠C=180°-∠A-∠ABC=105°.
(2)∵DE∥BC,
∴∠AED=∠ABC=30°.
∵∠BED+∠AED=180°,
∴∠BED=180°-∠AED=150°.
18.证明:∵∠E=∠F,
∴AE∥CF,
∴∠A=∠ABF,
∵∠A=∠C,
∴∠ABF=∠C,
∴AB∥CD.
19.解:(1)CD∥EF.
∵CD⊥AB,EF⊥AB,
∴∠BFE=∠BDC=90°,
∴CD∥EF;
(2)由(1)可知CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC,
∴∠ACB=∠3,
∴∠3=110°,
∴∠ACB=110°.
20.解:(1)如图所示:△A′B′C′,即为所求;
(2)AA′与CC′,平行且相等;
(3)如图所示:BD,即为所求;
(4)如图所示:CE,即为所求;
(5)△A′B′C′面积为:×4×5=10.
故答案为:10.
21.解:∵∠1=∠2,∠3=∠4,
∴∠4=2∠1=2∠2=∠3
∴∠2+∠3=3∠2=126°
∴∠2=∠1=42°
∴∠DAC=54°-42°=12°.
22.解:∵2019°÷180°=11,
∴这个多边形的内角和为180°×12=2160°,
∴这个内角的度数是:2160°-2019°=141°
设这个多边形的边数是n,由题意得:(n-2)×180°=2160°
解得:n=14
答:这个内角的度数为141°,多边形的边数为14.
23.解:AE∥CF.
理由如下:∵∠B=∠D=90°,
∴∠BAD+∠BCD=360°-90°×2=180°,
∵AE、CF分别平分∠BAD和∠BCD,
∴∠1=∠BAD,∠2=∠BCD,
∴∠1+∠2=(∠BAD+∠BCD)=×180°=90°,
∵∠B=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∴AE∥CF.
24.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°-(∠ABC+∠ACB)=180°-×100°=130°
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)=(360°-∠ABC-∠ACB)
=(180°+∠A)
=90°+∠A
∴∠Q=180°-(∠QBC+∠QCB)=180°-(90°+∠A )=90°-∠A;
(3)延长BC到F,如图所示
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ=∠ABC+∠MBC=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°-∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°-∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
2019.2.22
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
