18.1.2 平行四边形的判定(1)课件
图片预览




文档简介
人教版数学八年级下册
18.1.2平行四边形的判定(1)
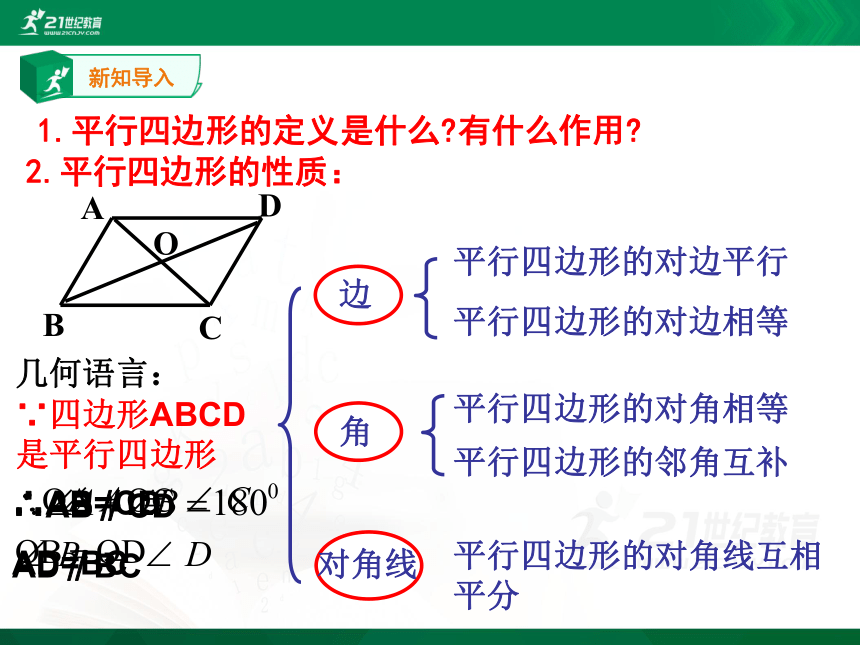
2.平行四边形的性质:
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
1.平行四边形的定义是什么?有什么作用?
几何语言:
我们知道了平行四边形的性质,那么,有
哪些方法可以判断一个四边形是平行四边形呢?
根据定义:两组对边分别平行的四边形
叫做平行四边形。
∵AB//CD , AD//BC
∴四边形ABCD是平行四边形
几何语言:
两组对边分别相等的
四边形是平行四边形
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:原命题正确,逆命题一定正确吗?
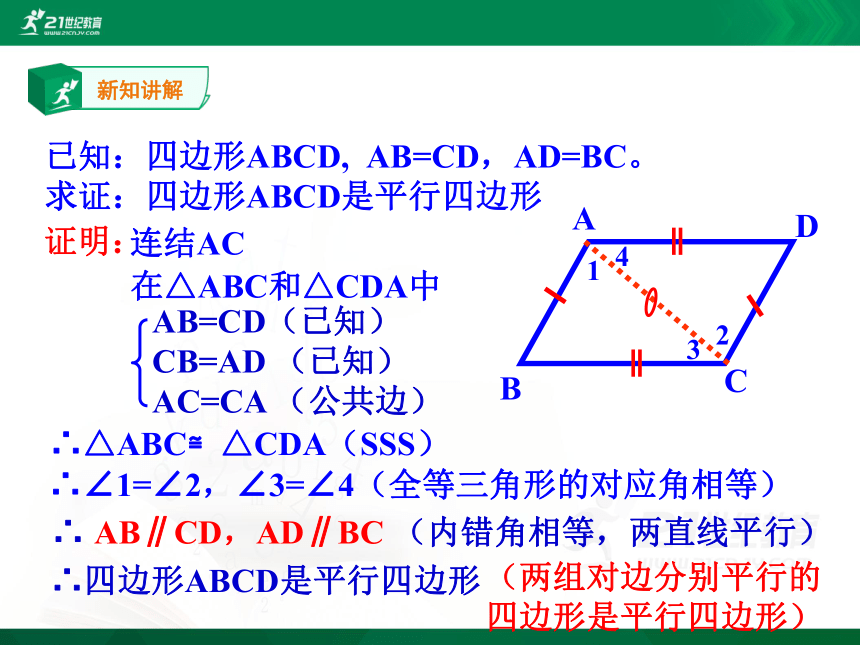
已知:四边形ABCD, AB=CD,AD=BC。
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
D
B
A
C
2
1
3
4
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
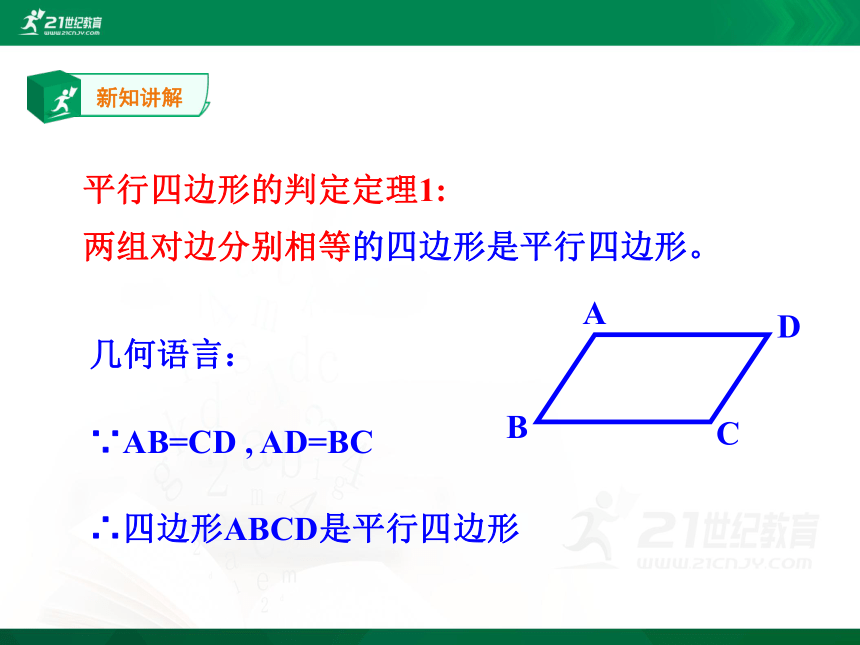
两组对边分别相等的四边形是平行四边形。
平行四边形的判定定理1:
几何语言:
∵AB=CD , AD=BC
∴四边形ABCD是平行四边形
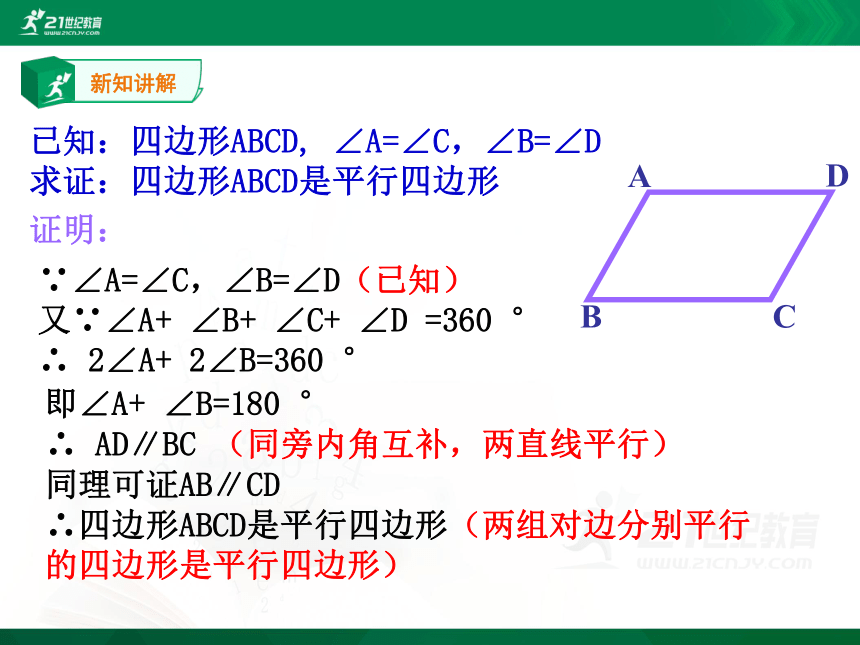
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
证明:
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
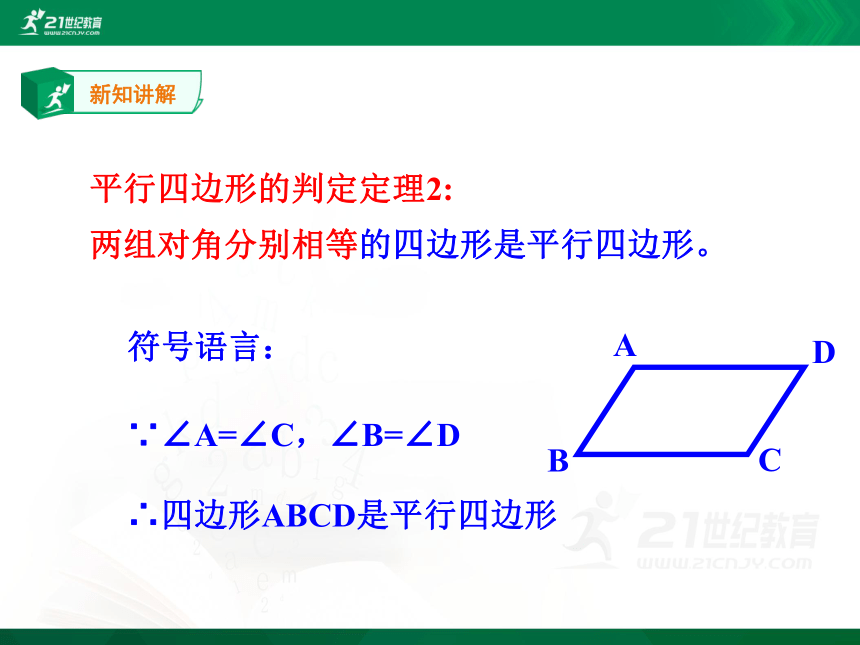
两组对角分别相等的四边形是平行四边形。
平行四边形的判定定理2:
符号语言:
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
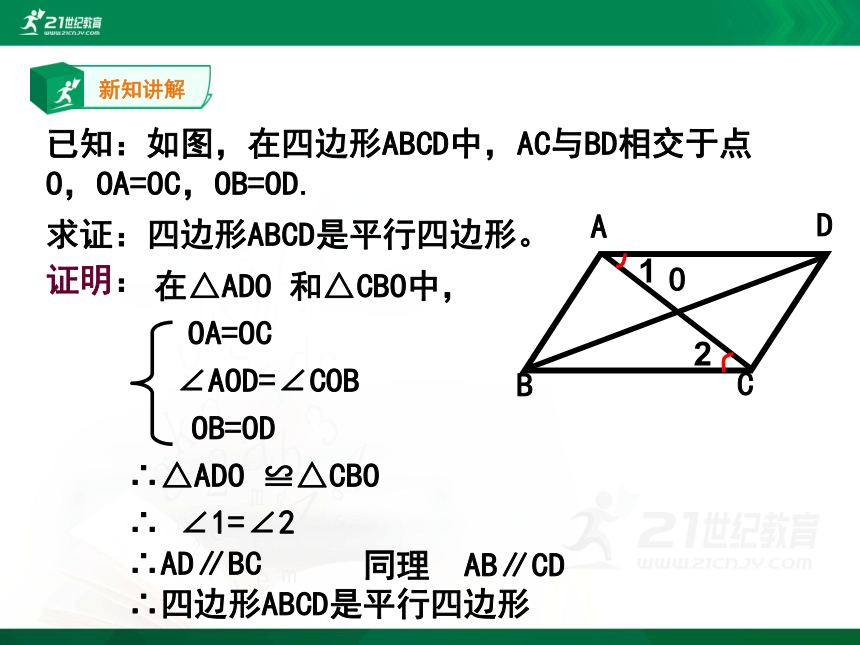
已知:如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD.
∴△ADO ≌△CBO
OA=OC
证明:
OB=OD
∠AOD=∠COB
∴四边形ABCD是平行四边形
求证:四边形ABCD是平行四边形。
O
2
1
在△ADO 和△CBO中,
∴ ∠1=∠2
∴AD∥BC
同理 AB∥CD
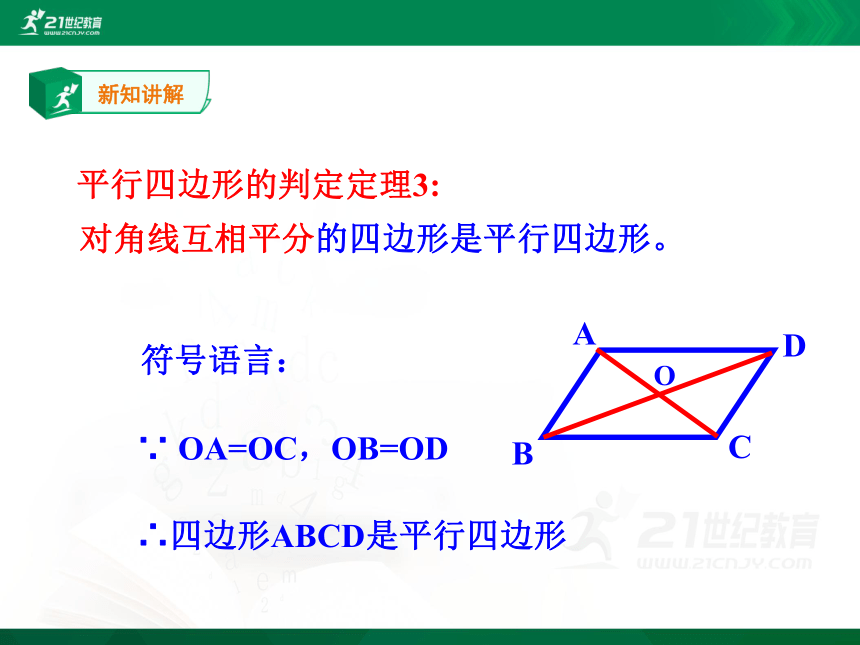
对角线互相平分的四边形是平行四边形。
平行四边形的判定定理3:
符号语言:
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(1)根据定义:两组对边分别平行的四边形叫做平行四边形.
(2)两组对边分别相等的四边形是平行四边形。
(3)两组对角分别相等的四边形是平行四边形。
(4)两条对角线互相平分的四边形是平行四边形。
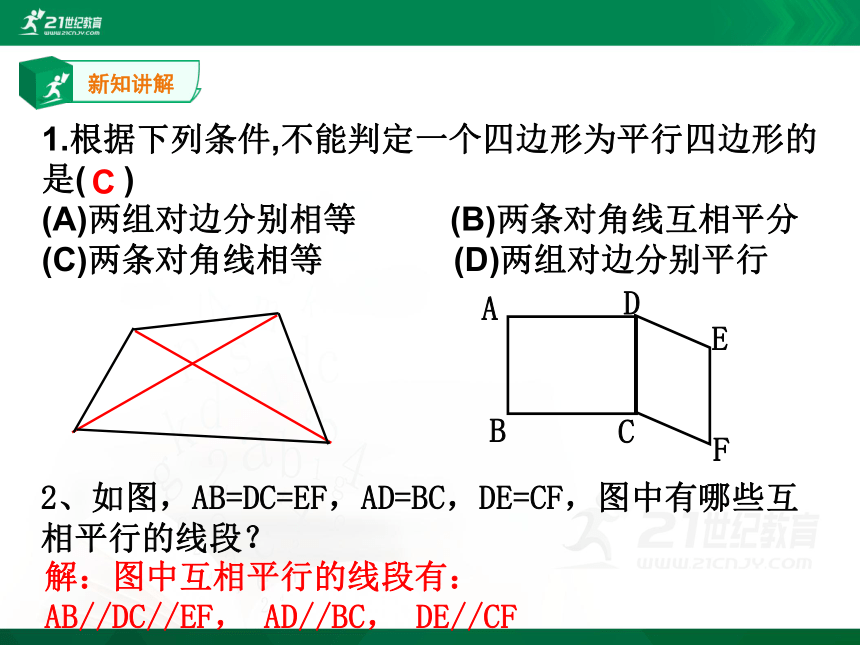
1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等 (B)两条对角线互相平分
(C)两条对角线相等 (D)两组对边分别平行
C
2、如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?
解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF
例1 如图:平行四边形ABCD的对角线AC、BD相交 于点O,E、F是AC上的两点,并且AE=CF,求证: 四边形BFDE是平行四边形。
你还有其他的证明方法吗?
证明:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
变式1 已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF。
求证:四边形BFDE是平行四边形。
O
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ BO=DO
∴EO=FO
∴ 四边形BFDE是平行四边形
O
变式2 如图:平行四边形ABCD的对角线AC、BD相交于点O,点E,F 分别在AC 两侧的延长线上,并且AE=CF.
求证: 四边形BFDE是平行四边形。
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是什么样的图形?
四边形ABCD是平行四边形
猜测:一组对边平行且相等的四边形是平行四边形。
你能证明吗?
已知:四边形ABCD中 AB∥CD, AB=CD。
求证:四边形ABCD是平行四边形。
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又∵AB =CD ,BD = DB
∴△ABD ≌△CDB (SAS)
∴AD = CB
∴四边形ABCD是平行四边形
又∵AB =CD
符号语言:
平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形。
在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由.
例2 如图,在 ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.
练习 如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.
例3 如图,分别以Rt△ABC的直角边AC及斜边AB
向外作等边△ACD、等边△ABE.且∠BAC=30°,EF
⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
例4 已知:平行四边形ABCD,对角线AC、BD相交于点O,E、F分别为OA、OC中点,求证:四边形BEDF是平行四边形。
C
A
D
B
E
H
F
O
G
你还有其他的证明方法吗?
若将“E、F分别为OA、OC中点”改为“AE=CF”,四边形BEDF还是平行四边形吗?
练习:平行四边形ABCD,对角线AC、BD相交于点O,AE=CF,求证:四边BEDF是平行四边形。
还可以是:①AF=CE
②∠ADE=∠CBF
③∠CDE=∠ABF
④BE⊥AC,DF⊥AC
……
试试看:你还能怎样改?
A
D
B
C
O
BE∥DF
一组对边平行,另一组对边相等的四边形是平行四边形吗?是,请说明理由;不是,请举出反例。
辩一辩:
AD∥BC且AB=DC,但四边形ABCD不是平行四边形。
不一定是,如:等腰梯形
1、请你识别下列四边形哪些是平行四边形?为什么?
⑴
⑷
⑶
⑵
从边来判定:
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定:
两组对角分别相等的四边形是平行四边形
从对角线来判定:
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
2、补充一个合适的条件使⑴—⑶小题成立:
4、在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm,CD= ____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=18cm,那么当AO=___ cm,DO= ____cm时,四边形ABCD为平行四边形.
A
B
C
D
O
8㎝
4㎝
8
4
5
9
以三角形任两边为邻边作平行四边形可作几个?
小游戏:看谁反应快?
A
B
C
作业
1.课本P50页第4、5、6 题
2.练习册 P 20-23 页
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
18.1.2平行四边形的判定(1)
2.平行四边形的性质:
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
1.平行四边形的定义是什么?有什么作用?
几何语言:
我们知道了平行四边形的性质,那么,有
哪些方法可以判断一个四边形是平行四边形呢?
根据定义:两组对边分别平行的四边形
叫做平行四边形。
∵AB//CD , AD//BC
∴四边形ABCD是平行四边形
几何语言:
两组对边分别相等的
四边形是平行四边形
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:原命题正确,逆命题一定正确吗?
已知:四边形ABCD, AB=CD,AD=BC。
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
D
B
A
C
2
1
3
4
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形。
平行四边形的判定定理1:
几何语言:
∵AB=CD , AD=BC
∴四边形ABCD是平行四边形
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
证明:
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对角分别相等的四边形是平行四边形。
平行四边形的判定定理2:
符号语言:
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
已知:如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD.
∴△ADO ≌△CBO
OA=OC
证明:
OB=OD
∠AOD=∠COB
∴四边形ABCD是平行四边形
求证:四边形ABCD是平行四边形。
O
2
1
在△ADO 和△CBO中,
∴ ∠1=∠2
∴AD∥BC
同理 AB∥CD
对角线互相平分的四边形是平行四边形。
平行四边形的判定定理3:
符号语言:
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(1)根据定义:两组对边分别平行的四边形叫做平行四边形.
(2)两组对边分别相等的四边形是平行四边形。
(3)两组对角分别相等的四边形是平行四边形。
(4)两条对角线互相平分的四边形是平行四边形。
1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等 (B)两条对角线互相平分
(C)两条对角线相等 (D)两组对边分别平行
C
2、如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?
解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF
例1 如图:平行四边形ABCD的对角线AC、BD相交 于点O,E、F是AC上的两点,并且AE=CF,求证: 四边形BFDE是平行四边形。
你还有其他的证明方法吗?
证明:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
变式1 已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF。
求证:四边形BFDE是平行四边形。
O
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ BO=DO
∴EO=FO
∴ 四边形BFDE是平行四边形
O
变式2 如图:平行四边形ABCD的对角线AC、BD相交于点O,点E,F 分别在AC 两侧的延长线上,并且AE=CF.
求证: 四边形BFDE是平行四边形。
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是什么样的图形?
四边形ABCD是平行四边形
猜测:一组对边平行且相等的四边形是平行四边形。
你能证明吗?
已知:四边形ABCD中 AB∥CD, AB=CD。
求证:四边形ABCD是平行四边形。
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又∵AB =CD ,BD = DB
∴△ABD ≌△CDB (SAS)
∴AD = CB
∴四边形ABCD是平行四边形
又∵AB =CD
符号语言:
平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形。
在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由.
例2 如图,在 ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.
练习 如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.
例3 如图,分别以Rt△ABC的直角边AC及斜边AB
向外作等边△ACD、等边△ABE.且∠BAC=30°,EF
⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
例4 已知:平行四边形ABCD,对角线AC、BD相交于点O,E、F分别为OA、OC中点,求证:四边形BEDF是平行四边形。
C
A
D
B
E
H
F
O
G
你还有其他的证明方法吗?
若将“E、F分别为OA、OC中点”改为“AE=CF”,四边形BEDF还是平行四边形吗?
练习:平行四边形ABCD,对角线AC、BD相交于点O,AE=CF,求证:四边BEDF是平行四边形。
还可以是:①AF=CE
②∠ADE=∠CBF
③∠CDE=∠ABF
④BE⊥AC,DF⊥AC
……
试试看:你还能怎样改?
A
D
B
C
O
BE∥DF
一组对边平行,另一组对边相等的四边形是平行四边形吗?是,请说明理由;不是,请举出反例。
辩一辩:
AD∥BC且AB=DC,但四边形ABCD不是平行四边形。
不一定是,如:等腰梯形
1、请你识别下列四边形哪些是平行四边形?为什么?
⑴
⑷
⑶
⑵
从边来判定:
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定:
两组对角分别相等的四边形是平行四边形
从对角线来判定:
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
2、补充一个合适的条件使⑴—⑶小题成立:
4、在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm,CD= ____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=18cm,那么当AO=___ cm,DO= ____cm时,四边形ABCD为平行四边形.
A
B
C
D
O
8㎝
4㎝
8
4
5
9
以三角形任两边为邻边作平行四边形可作几个?
小游戏:看谁反应快?
A
B
C
作业
1.课本P50页第4、5、6 题
2.练习册 P 20-23 页
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
