广东省深圳市耀华实验学校2018-2019学年高一下学期入学考试数学试题(国际1班) Word版含答案
文档属性
| 名称 | 广东省深圳市耀华实验学校2018-2019学年高一下学期入学考试数学试题(国际1班) Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 190.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 00:00:00 | ||
图片预览



文档简介
耀华实验学校2018—2019 第二学期高一入学考试
数学试卷(高一国1用)
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,则( ).
. . . .
2. 下列四个函数中,在(0,+∞)上为增函数的是 ( ).
A. B. C. D.
3.下列四组函数中,表示同一函数的是 ( ).
A. B.
C. D.
4. 如图,U是全集,集合、是集合U的两个子集,则阴影部
分所表示的集合是 ( ).
A. A∩(?U B) B. ?U(A∩B)
C. (?U A)∩(?U B) D. (?U A)∩B
5.若,则 ( ).
A.0 B.1
C. D.1或
6.已知函数在区间(-∞,3]上递减,则的取值范围是 ( ).
A.[2+∞) B.(-∞,2)
C.(-∞,2] D.(2,+∞)
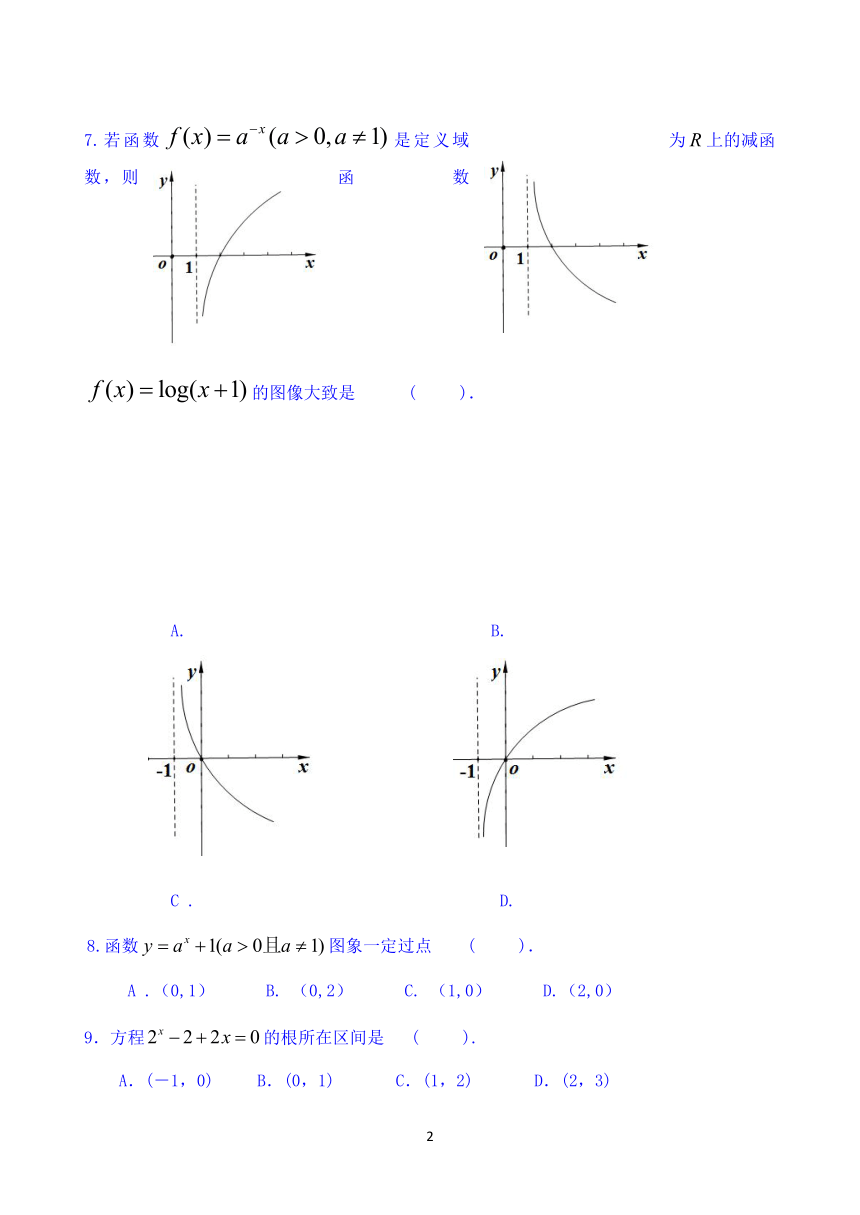
7.若函数是定义域为上的减函数,则函数的图像大致是 ( ).
A. B.
C . D.
8.函数图象一定过点 ( ).
A .(0,1) B. (0,2) C. (1,0) D.(2,0)
9.方程的根所在区间是 ( ).
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
10.设,,,则 ( ).
A. B.
C. D.
11. 已知函数=的定义域是一切实数,则的取值范围是 ( ).
A. B. C. D.
12.已知函数是上的偶函数,且在上单调递减,则下列各式成立的是 ( ).
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.计算 .
14.函数的定义域为 .
15.已知幂函数的图像过点,则 .
16.2017年国庆期间,某商店将彩电价格由原价(3250元/台)提高35%,然后在广告上写出“大酬宾八折优惠”,则商店每台彩电比原价多卖 元.
三、解答题(本大题共6小题共70分,解答应写出文字说明,证明过程或演算步骤。把答案写在答题卡上相应位置。)
17.(本小题满分10分)若集合和
(1)当时,求集合A∩B;
(2)当B?A时,求实数m的取值范围.
18.(本小题满分12分)已知函数.
(1)求、、的值;
(2)若,求的值.
19. (本小题满分12分)已知函数.
(1)求的定义域,并判断的奇偶性;
(2)判断的单调性,并用定义证明你的结论.
20.(本小题满分12分)二次函数满足且.
? (1)??? 求的解析式;
??? (2)?? 若在区间上上恒成立,,试确定实数的 取值范围.
21.(本小题满分12分)近年来,由于用电紧张,用电成本增加,某地供电局为鼓励居民节约用电,电价按等级逐级递增。规定:每月用电量不超过210度(千瓦时)的部分,电价为0.54元/度;每月用电量超过210度但不超过400度的部分,电价为0.60元/度;每月用电量超过400度的部分,电价为0.84元/度.
(1)试用分段函数写出居民应缴纳电费y与用电量的函数关系;
(2)已知某居民某月交纳电费为269.4元,那么他当月用电量是多少?
22.(本小题满分12分)设,
(1)若,试求:的值;
(2)求的值.
参考答案
选择题:
1
2
3
4
5
6
7
8
9
10
11
12
D
C
A
D
C
C
D
B
B
A
B
A
二、填空题:
5 14. 15. 8 16. 260
三、解答题:
17.解:(1)当时,.
=, ..........5分
若,则解得
的取值范围时. .........10分
解:(1)由题可知,
..........6分
当时,得(满足)
当时,得(满足)
当时,得(舍去)
综上所述,的值为或. ..........12分
解:(1)由得,
的定义域为;
对于定义域内的每一个都有
是奇函数. ..........6分
任取且则
,又
,,
,是减函数. ..........12分
解:(1)设
,
解得 ..........6分
由(1)知,由得,
,令,只需在上是减函数,在上是增函数,,即
的取值范围是. ..........12分
解:(1) 由题意可知与的函数关系为:
即 ..........7分
由题意即(1)可知
由解得
所以,该居民当月用电量为450度. ..........12分
解:(1)由题可知
; ..........6分
由(1)知,所以即
,同理可得,,......
所以,.
..........12分
数学试卷(高一国1用)
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,则( ).
. . . .
2. 下列四个函数中,在(0,+∞)上为增函数的是 ( ).
A. B. C. D.
3.下列四组函数中,表示同一函数的是 ( ).
A. B.
C. D.
4. 如图,U是全集,集合、是集合U的两个子集,则阴影部
分所表示的集合是 ( ).
A. A∩(?U B) B. ?U(A∩B)
C. (?U A)∩(?U B) D. (?U A)∩B
5.若,则 ( ).
A.0 B.1
C. D.1或
6.已知函数在区间(-∞,3]上递减,则的取值范围是 ( ).
A.[2+∞) B.(-∞,2)
C.(-∞,2] D.(2,+∞)
7.若函数是定义域为上的减函数,则函数的图像大致是 ( ).
A. B.
C . D.
8.函数图象一定过点 ( ).
A .(0,1) B. (0,2) C. (1,0) D.(2,0)
9.方程的根所在区间是 ( ).
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
10.设,,,则 ( ).
A. B.
C. D.
11. 已知函数=的定义域是一切实数,则的取值范围是 ( ).
A. B. C. D.
12.已知函数是上的偶函数,且在上单调递减,则下列各式成立的是 ( ).
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.计算 .
14.函数的定义域为 .
15.已知幂函数的图像过点,则 .
16.2017年国庆期间,某商店将彩电价格由原价(3250元/台)提高35%,然后在广告上写出“大酬宾八折优惠”,则商店每台彩电比原价多卖 元.
三、解答题(本大题共6小题共70分,解答应写出文字说明,证明过程或演算步骤。把答案写在答题卡上相应位置。)
17.(本小题满分10分)若集合和
(1)当时,求集合A∩B;
(2)当B?A时,求实数m的取值范围.
18.(本小题满分12分)已知函数.
(1)求、、的值;
(2)若,求的值.
19. (本小题满分12分)已知函数.
(1)求的定义域,并判断的奇偶性;
(2)判断的单调性,并用定义证明你的结论.
20.(本小题满分12分)二次函数满足且.
? (1)??? 求的解析式;
??? (2)?? 若在区间上上恒成立,,试确定实数的 取值范围.
21.(本小题满分12分)近年来,由于用电紧张,用电成本增加,某地供电局为鼓励居民节约用电,电价按等级逐级递增。规定:每月用电量不超过210度(千瓦时)的部分,电价为0.54元/度;每月用电量超过210度但不超过400度的部分,电价为0.60元/度;每月用电量超过400度的部分,电价为0.84元/度.
(1)试用分段函数写出居民应缴纳电费y与用电量的函数关系;
(2)已知某居民某月交纳电费为269.4元,那么他当月用电量是多少?
22.(本小题满分12分)设,
(1)若,试求:的值;
(2)求的值.
参考答案
选择题:
1
2
3
4
5
6
7
8
9
10
11
12
D
C
A
D
C
C
D
B
B
A
B
A
二、填空题:
5 14. 15. 8 16. 260
三、解答题:
17.解:(1)当时,.
=, ..........5分
若,则解得
的取值范围时. .........10分
解:(1)由题可知,
..........6分
当时,得(满足)
当时,得(满足)
当时,得(舍去)
综上所述,的值为或. ..........12分
解:(1)由得,
的定义域为;
对于定义域内的每一个都有
是奇函数. ..........6分
任取且则
,又
,,
,是减函数. ..........12分
解:(1)设
,
解得 ..........6分
由(1)知,由得,
,令,只需在上是减函数,在上是增函数,,即
的取值范围是. ..........12分
解:(1) 由题意可知与的函数关系为:
即 ..........7分
由题意即(1)可知
由解得
所以,该居民当月用电量为450度. ..........12分
解:(1)由题可知
; ..........6分
由(1)知,所以即
,同理可得,,......
所以,.
..........12分
同课章节目录
