安徽省定远重点中学2018-2019学年高一下学期开学考试数学试题 Word版含答案
文档属性
| 名称 | 安徽省定远重点中学2018-2019学年高一下学期开学考试数学试题 Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 188.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 00:00:00 | ||
图片预览

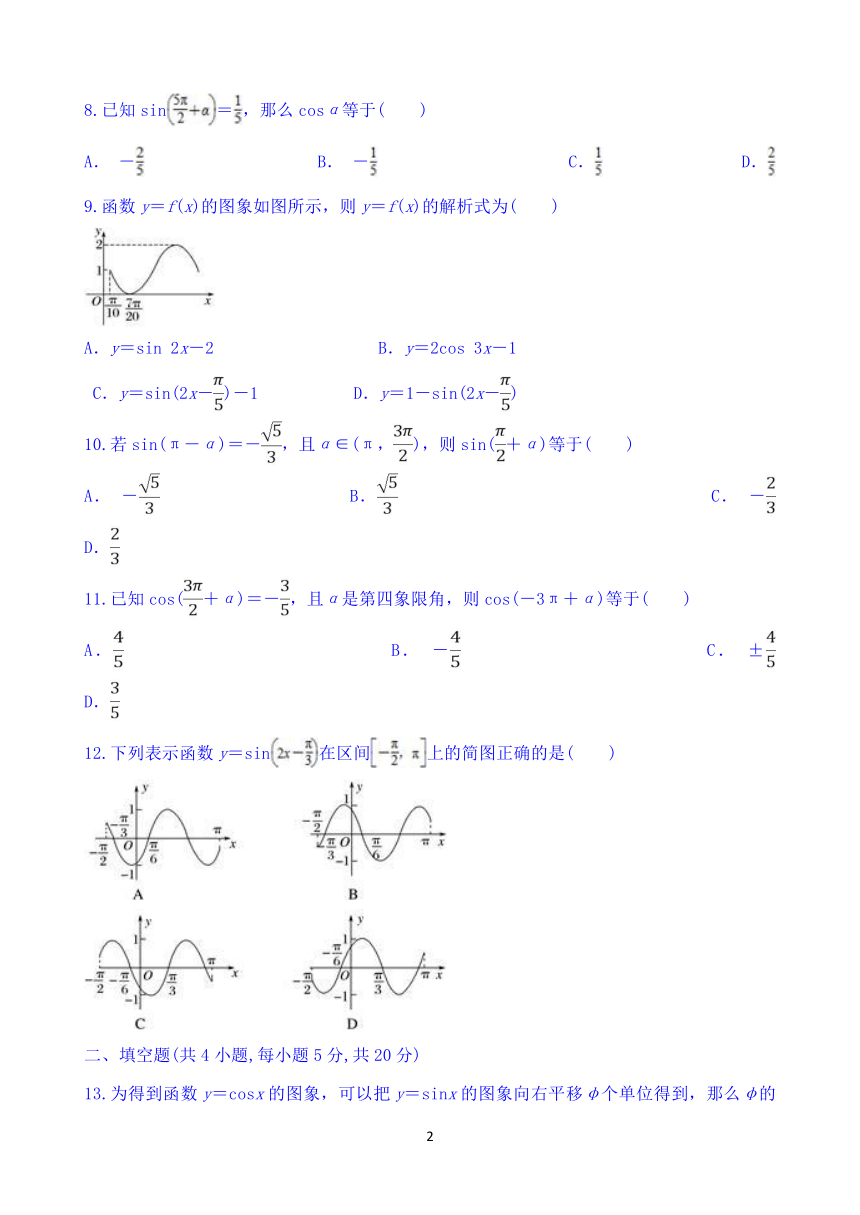

文档简介
2018-2019学年度第二学期开学考试
高一数学试题
本试卷共150分,考试时间120分钟。
一、选择题(共12小题,每小题5分,共60分)
1.设全集U=R,集合A={x|x≤1或x≥3},集合B={x|kA.k<0或k>3 B. 22.已知g(x)=1-2x,f(g(x))=(x≠0),则f()等于( )
A. 1 B. 3 C. 15 D. 30
3.已知f(x)是偶函数,对任意的x1,x2∈(-∞,-1],都有(x2-x1)[f(x2)-f(x1)]<0,则下列关系式中成立的是( )
A.f4.函数y=2x-x2的图象大致是( )
5.若φ(x),g(x)都是奇函数,f(x)=aφ(x)+bg(x)+3在(0,+∞)上有最大值10,则f(x)在(-∞,0)上有( )
A. 最小值-4 B. 最大值-4 C. 最小值-1 D. 最大值-3
6.已知函数f(x)=且f(a)=-3,则f(6-a)等于( )
A. - B. - C. - D. -
7.若点P(3,y)是角α终边上的一点,且满足y<0,cosα=,则tanα等于( )
A. - B. C. D. -
8.已知sin=,那么cosα等于( )
A. - B. - C. D.
9.函数y=f(x)的图象如图所示,则y=f(x)的解析式为( )
A.y=sin 2x-2 B.y=2cos 3x-1
C.y=sin(2x-)-1 D.y=1-sin(2x-)
10.若sin(π-α)=-,且α∈(π,),则sin(+α)等于( )
A. - B. C. - D.
11.已知cos(+α)=-,且α是第四象限角,则cos(-3π+α)等于( )
A. B. - C. ± D.
12.下列表示函数y=sin在区间上的简图正确的是( )
二、填空题(共4小题,每小题5分,共20分)
13.为得到函数y=cosx的图象,可以把y=sinx的图象向右平移φ个单位得到,那么φ的最小正值是________.
14.若sin(-α)=,则cos(+2α)=________.
15.函数f(x)=lnx+x2-3的零点x0与的大小关系为________.
16.已知函数y=f(x)+x3为偶函数,且f(10)=10,若函数g(x)=f(x)+4,则g(-10)=___________.
三、解答题(共6小题,共70分)
17. (12分) 设全集U=R,A={x|x2+x-20<0},B={x||2x+5|>7},C={x|x2-3mx+2m2<0}.
(1)若C?(A∩B),求m的取值范围;
(2)若(?UA)∩(?UB)?C,求m的取值范围.
18. (10分) 已知角为第三象限角, ,
若,求的值.
19. (12分)已知函数f(x)=log2(2x+1).
(1)求证:函数f(x)在(-∞,+∞)内单调递增;
(2)若g(x)=log2(2x-1)(x>0),且关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.
20. (12分)已知函数f(x)=2x+2ax+b,且f(1)=,f(2)=.
(1)求a,b的值;
(2)判断f(x)的奇偶性并证明;
(3)先判断并证明函数f(x)在[0,+∞)上的单调性.
21. (10分)已知函数 . (1)求函数 的最小正周期; (2)求函数 在区间 上的最大值和最小值.
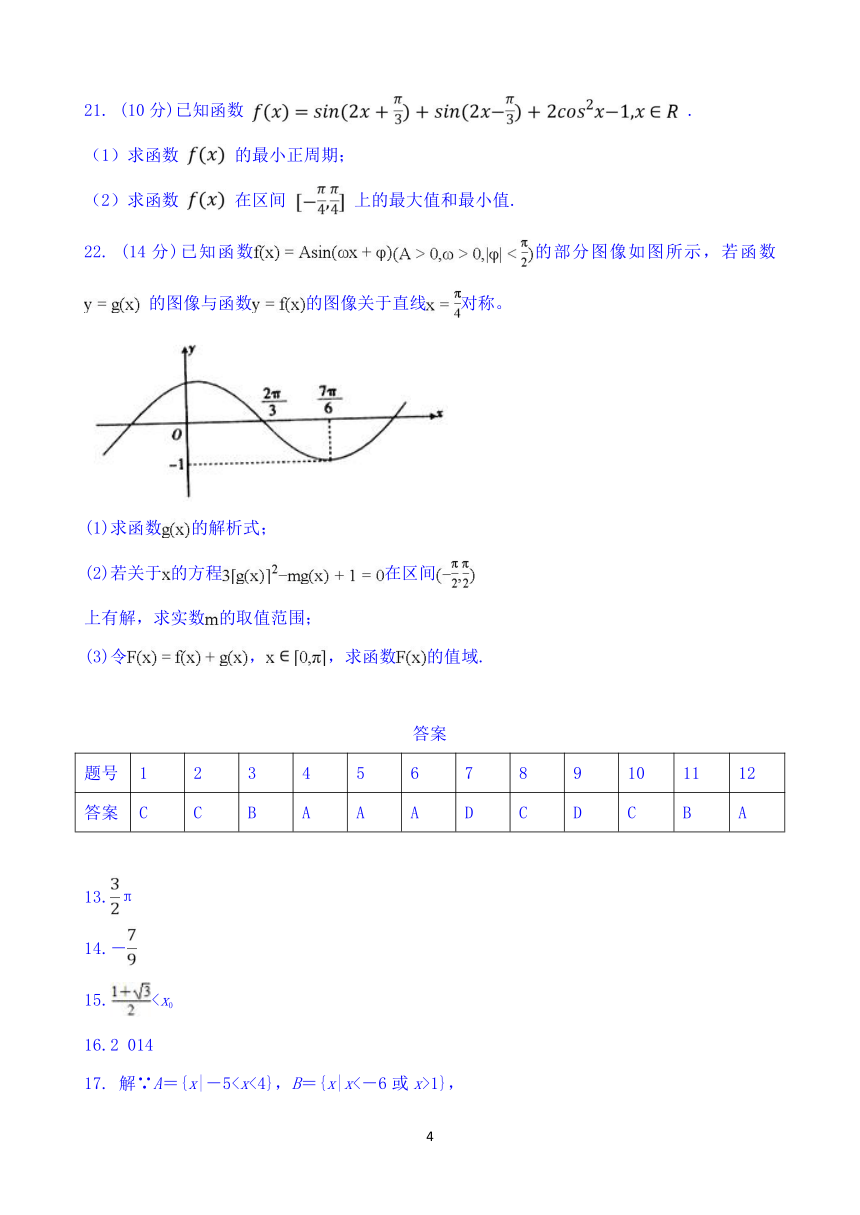
22. (14分)已知函数的部分图像如图所示,若函数 的图像与函数的图像关于直线对称。
(1)求函数的解析式;
(2)若关于的方程在区间
上有解,求实数的取值范围;
(3)令,,求函数的值域.
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
B
A
A
A
D
C
D
C
B
A
13.π
14.-
15.16.2 014
17. 解∵A={x|-51},
∵x2-3mx+2m2=(x-m)(x-2m)<0.
(1)A∩B={x|1∵C?(A∩B),
当m=0时,C=?,满足题意;
当m<0时,不合题意;
当m>0时,C={x|m综上,m=0或1≤m≤2.
(2)(?UA)∩(?UB)={x|-6≤x≤-5},
∵(?UA)∩(?UB)?C,∴C≠?,∴m≠0.
当m>0时,不合题意;
当m<0时,C={x|2m18.
解析: ,
,从而 ,
又 为第三象限角,则 ,
即 的值为 .
19.(1)证明 因为函数f(x)=log2(2x+1),
任取x1则f(x1)-f(x2)=log2(2x1+1)-log2(2x2+1)=log2,
因为x1所以log2<0,
所以f(x1)所以函数f(x)在(-∞,+∞)内单调递增.
(2)解 g(x)=m+f(x),即g(x)-f(x)=m.
设h(x)=g(x)-f(x)
=log2(2x-1)-log2(2x+1)
=log2
=log2.
设1≤x1则3≤2x1+1<2x2+1≤5,
≥>≥,
-≤<≤-,
∴≤1-<1-≤,∴log2≤h(x1)即h(x)在[1,2]上为增函数且值域为[log2,log2].
要使g(x)-f(x)=m有解,需m∈[log2,log2].
20. 解(1)??
(2)f(x)=2x+2-x,f(x)的定义域为R,
f(-x)=2-x+2x=f(x),所以f(x)为偶函数.
(3)函数f(x)在[0,+∞)上是增函数,证明如下:
任取x1f(x1)-f(x2)=(+)-(+)
=(-)+(-)=(-)·,
因为x1所以-<0,>1,
所以f(x1)-f(x2)<0,
所以f(x)在[0,+∞)上为增函数.
21. 解:(1) ,所以f(x)的最小正周期 (2)易知 在区间 上是增函数,在区间 上是减函数. 故函数 在区间 上的最大值为 ,最小值为
22.(1);(2);(3).
解析:(1)由图可知,,
,,,,
由于,故即.
。
(2),,即.
又,,
①当时,;
②当时,;
③当时,;
综上,实数的取值范围是
(3) ,
。
又,,,
即,
函数函数的值域为。
高一数学试题
本试卷共150分,考试时间120分钟。
一、选择题(共12小题,每小题5分,共60分)
1.设全集U=R,集合A={x|x≤1或x≥3},集合B={x|k
A. 1 B. 3 C. 15 D. 30
3.已知f(x)是偶函数,对任意的x1,x2∈(-∞,-1],都有(x2-x1)[f(x2)-f(x1)]<0,则下列关系式中成立的是( )
A.f
5.若φ(x),g(x)都是奇函数,f(x)=aφ(x)+bg(x)+3在(0,+∞)上有最大值10,则f(x)在(-∞,0)上有( )
A. 最小值-4 B. 最大值-4 C. 最小值-1 D. 最大值-3
6.已知函数f(x)=且f(a)=-3,则f(6-a)等于( )
A. - B. - C. - D. -
7.若点P(3,y)是角α终边上的一点,且满足y<0,cosα=,则tanα等于( )
A. - B. C. D. -
8.已知sin=,那么cosα等于( )
A. - B. - C. D.
9.函数y=f(x)的图象如图所示,则y=f(x)的解析式为( )
A.y=sin 2x-2 B.y=2cos 3x-1
C.y=sin(2x-)-1 D.y=1-sin(2x-)
10.若sin(π-α)=-,且α∈(π,),则sin(+α)等于( )
A. - B. C. - D.
11.已知cos(+α)=-,且α是第四象限角,则cos(-3π+α)等于( )
A. B. - C. ± D.
12.下列表示函数y=sin在区间上的简图正确的是( )
二、填空题(共4小题,每小题5分,共20分)
13.为得到函数y=cosx的图象,可以把y=sinx的图象向右平移φ个单位得到,那么φ的最小正值是________.
14.若sin(-α)=,则cos(+2α)=________.
15.函数f(x)=lnx+x2-3的零点x0与的大小关系为________.
16.已知函数y=f(x)+x3为偶函数,且f(10)=10,若函数g(x)=f(x)+4,则g(-10)=___________.
三、解答题(共6小题,共70分)
17. (12分) 设全集U=R,A={x|x2+x-20<0},B={x||2x+5|>7},C={x|x2-3mx+2m2<0}.
(1)若C?(A∩B),求m的取值范围;
(2)若(?UA)∩(?UB)?C,求m的取值范围.
18. (10分) 已知角为第三象限角, ,
若,求的值.
19. (12分)已知函数f(x)=log2(2x+1).
(1)求证:函数f(x)在(-∞,+∞)内单调递增;
(2)若g(x)=log2(2x-1)(x>0),且关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.
20. (12分)已知函数f(x)=2x+2ax+b,且f(1)=,f(2)=.
(1)求a,b的值;
(2)判断f(x)的奇偶性并证明;
(3)先判断并证明函数f(x)在[0,+∞)上的单调性.
21. (10分)已知函数 . (1)求函数 的最小正周期; (2)求函数 在区间 上的最大值和最小值.
22. (14分)已知函数的部分图像如图所示,若函数 的图像与函数的图像关于直线对称。
(1)求函数的解析式;
(2)若关于的方程在区间
上有解,求实数的取值范围;
(3)令,,求函数的值域.
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
B
A
A
A
D
C
D
C
B
A
13.π
14.-
15.
17. 解∵A={x|-5
∵x2-3mx+2m2=(x-m)(x-2m)<0.
(1)A∩B={x|1
当m=0时,C=?,满足题意;
当m<0时,不合题意;
当m>0时,C={x|m
(2)(?UA)∩(?UB)={x|-6≤x≤-5},
∵(?UA)∩(?UB)?C,∴C≠?,∴m≠0.
当m>0时,不合题意;
当m<0时,C={x|2m
解析: ,
,从而 ,
又 为第三象限角,则 ,
即 的值为 .
19.(1)证明 因为函数f(x)=log2(2x+1),
任取x1
因为x1
所以f(x1)
(2)解 g(x)=m+f(x),即g(x)-f(x)=m.
设h(x)=g(x)-f(x)
=log2(2x-1)-log2(2x+1)
=log2
=log2.
设1≤x1
≥>≥,
-≤<≤-,
∴≤1-<1-≤,∴log2≤h(x1)
要使g(x)-f(x)=m有解,需m∈[log2,log2].
20. 解(1)??
(2)f(x)=2x+2-x,f(x)的定义域为R,
f(-x)=2-x+2x=f(x),所以f(x)为偶函数.
(3)函数f(x)在[0,+∞)上是增函数,证明如下:
任取x1
=(-)+(-)=(-)·,
因为x1
所以f(x1)-f(x2)<0,
所以f(x)在[0,+∞)上为增函数.
21. 解:(1) ,所以f(x)的最小正周期 (2)易知 在区间 上是增函数,在区间 上是减函数. 故函数 在区间 上的最大值为 ,最小值为
22.(1);(2);(3).
解析:(1)由图可知,,
,,,,
由于,故即.
。
(2),,即.
又,,
①当时,;
②当时,;
③当时,;
综上,实数的取值范围是
(3) ,
。
又,,,
即,
函数函数的值域为。
同课章节目录
