北师大版2018-2019学年七年级下数学课时同步练习卷:1.5 平方差公式(附答案)
文档属性
| 名称 | 北师大版2018-2019学年七年级下数学课时同步练习卷:1.5 平方差公式(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 174.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 08:21:34 | ||
图片预览

文档简介
1.5 平方差公式
一、填空题(共10题;共30分)
1.计算:(2a+b)(2a-b)- =________.
2.计算:(x+1)2﹣(x+2)(x﹣2)=________.
3.两个正方形的边长和为20cm,它们的面积的差为40cm2 , 则这两个正方形的边长差为________ cm
4.若a+b=﹣3,ab=2,则a2+b2=________?
5. 已知,,则值为________.
6.(﹣x﹣11y)( ________?)=﹣121y2 .
7.化简:(m+n)(m﹣n)+2n2=________?
8.利用简便方法计算: =________.
9.计算:(x+4)(x﹣4)=________
10.在2001、2002、…、2010这10个数中,不能表示成两个平方数差的数有________个。
二、单选题(共10题;共30分)
11.下列各式能用平方差公式计算的是( ??)
A.?(2a+b)(2b-a)???????????????B.?(- x+1)(- x-1)???????????????C.?(a+b)(a-2b)???????????????D.?(2x-1)(-2x+1)
12.下列各式中不能用平方差公式计算的是(??? )
A.?(x-2y)(2y+x)???????????????B.?(x-2y)(-2y+x)???????????????C.?(x+y)(y-x)???????????????D.?(2x-3y)(3y+2x)
13.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图(1),然后拼成一个梯形,如图(2),根据这两个图形的面积关系,表明下列式子成立的是( )
A.?a2﹣b2=(a+b)(a﹣b)????????????????????????????????B.?(a+b)2=a2+2ab+b2
C.?(a﹣b)2=a2﹣2ab+b2???????????????????????????????????D.?a2﹣b2=(a﹣b)2
14.下列各式中,不能用平方差公式计算的是(?? )
A.?(﹣4x+3y)(4x+3y)????????????????????????????????????B.?(4x﹣3y)(3y﹣4x)??
C.?(﹣4x+3y)(﹣4x﹣3y)????????????????????????????????D.?(4x+3y)(4x﹣3y)
15.下列计算正确的一项是(?? )
A.?a5+a5=2a10???????????B.?(a+2)(a﹣2)=a2﹣4???????????C.?(a﹣b)2=a2﹣b2???????????D.?4a﹣2a=2
16.计算(a﹣b)(a+b)(a2+b2)(a4﹣b4)的结果是( )
A.?a8+2a4b4+b8???????????????????????B.?a8﹣2a4b4+b8???????????????????????C.?a8+b8???????????????????????D.?a8﹣b8
17. 下列算式能用平方差公式计算的是( )
A. B.
C. D.
18.下列乘法中,不能运用平方差公式进行运算的是( )
A.?(x+a)(x﹣a)???????????????????????????????????????????????B.?(﹣x﹣b)(x﹣b)
C.?(a+b)(﹣a﹣b)??????????????????????????????????????????D.?(b+m)(m﹣b)
19.计算(x﹣1)(﹣x﹣1)的结果是(?? )
A.?﹣x2+1????????????????????????????????B.?x2﹣1????????????????????????????????C.?﹣x2﹣1????????????????????????????????D.?x2+1
20.下列各式能用平方差公式计算的是( ??)???????
A.?(x+1)(x-1)????????B.?(a+b)(a-2b)????????C.?(-a+b)(a-b)????????D.?(-m-n)(m+n)
三、解答题(共9题;共60分)
21.先化简,再求值:(2x+1)(2x﹣1)﹣3x(x+1)﹣(x﹣1)2 , 当x=﹣1.
22.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”,如:4=22﹣02 , 12=42﹣22 , 20=62﹣42 , 因此4、12、20都是这种“神秘数”.
(1)28和2012这两个数是“神秘数”吗?试说明理由;
(2)试说明神秘数能被4整除;
(3)两个连续奇数的平方差是神秘数吗?试说明理由.
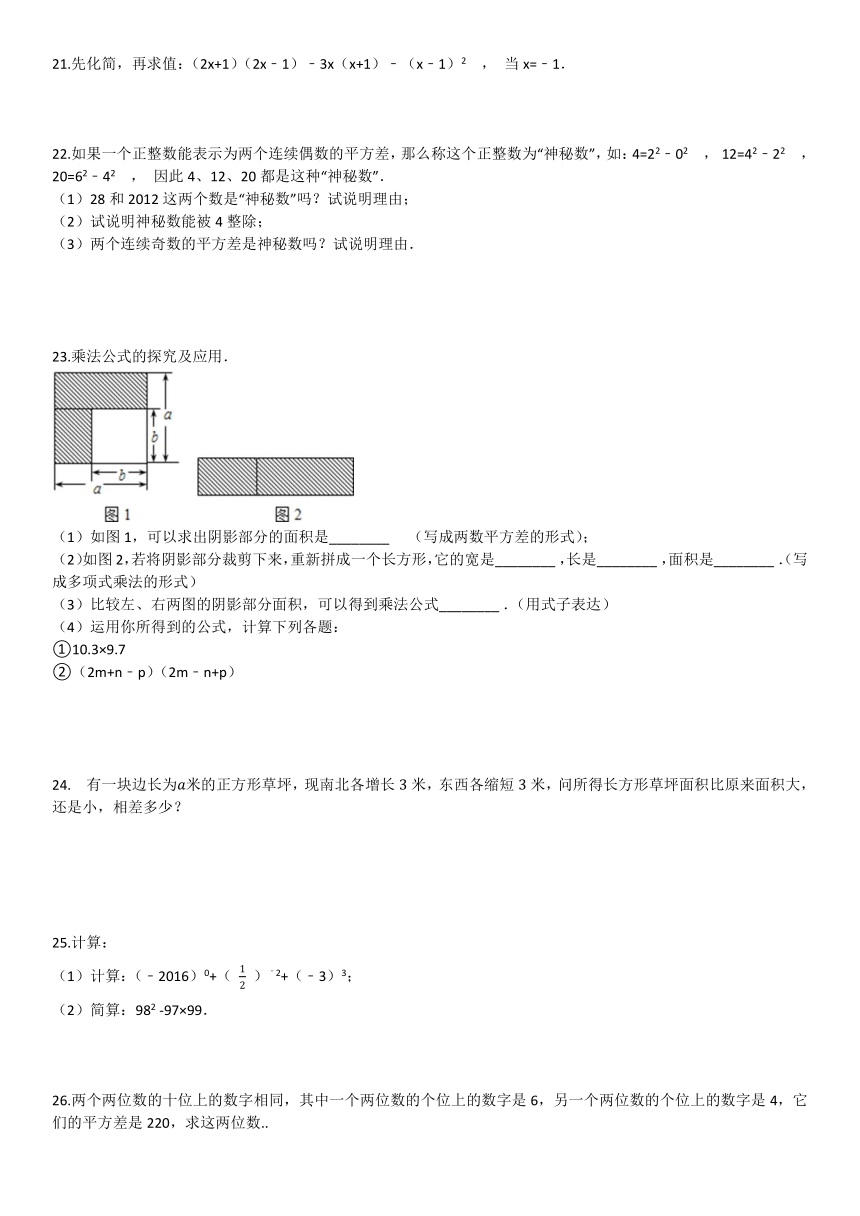
23.乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是________? (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是________?,长是________?,面积是________?.(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式________?.(用式子表达)
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
24. 有一块边长为米的正方形草坪,现南北各增长米,东西各缩短米,问所得长方形草坪面积比原来面积大,还是小,相差多少?
25.计算:
(1)计算:(﹣2016)0+( )﹣2+(﹣3)3;
(2)简算:982 -97×99.
26.两个两位数的十位上的数字相同,其中一个两位数的个位上的数字是6,另一个两位数的个位上的数字是4,它们的平方差是220,求这两位数..
27.一个单项式加上多项式9(x﹣1)2﹣2x﹣5后等于一个整式的平方,试求所有这样的单项式.
28.怎样简便就怎样计算:
(1)1232﹣124×122??????????????????????????
(2)(2a+b)(4a2+b2)(2a﹣b)
29.乘法公式的探究及应用:
(1)如图1所示,可以求出阴影部分面积是________?;(写成两数平方差的形式)
(2)若将图1中的阴影部分裁剪下来,重新拼成一个如图2的矩形,此矩形的面积是________?;(写成多项式乘法的形式)
(3)根据两图的阴影部分面积得到的乘法公式计算下列算式:
答案
一、填空题
1.【答案】3 +2ab-2
2.【答案】2x+5
3.【答案】2
4.【答案】5
5.【答案】±12
6.【答案】﹣x+11y
7.【答案】m2+n2
8.【答案】
9.【答案】x2﹣16
10.【答案】3
二、单选题
11.【答案】 B
12.【答案】 B
13.【答案】A
14.【答案】 B
15.【答案】B
16.【答案】 B
17.【答案】 D
18.【答案】C
19.【答案】 A
20.【答案】 A
三、解答题
21.【答案】解:原式=4x2﹣1﹣3x2﹣3x﹣x2+2x﹣1=﹣x﹣2,
当x=﹣1时,原式=1﹣2=﹣1.
22.【答案】解:(1)是,理由如下:
∵28=82﹣62 , 2012=5042﹣5022 ,
∴28是“神秘数”;2012是“神秘数”;
(2)“神秘数”是4的倍数.理由如下:
(2k+2)2﹣(2k)2=(2k+2+2k)(2k+2﹣2k)=2(4k+2)=4(2k+1),
∴“神秘数”是4的倍数;
(3)设两个连续的奇数为:2k+1,2k﹣1,则
(2k+1)2﹣(2k﹣1)2=8k,
而由(2)知“神秘数”是4的倍数,但不是8的倍数,
所以两个连续的奇数的平方差不是神秘数.
23.【答案】(1)a2﹣b2
(2)a﹣b;a+b;(a+b)(a﹣b)
(3)(a+b)(a﹣b)=a2﹣b2
(4)解:①原式=(10+0.3)×(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91;
②原式=[2m+(n﹣p)]?[2m﹣(n﹣p)]
=(2m)2﹣(n﹣p)2
=4m2﹣n2+2np﹣p2 .
24.【答案】解:根据题意得:
.
即所得长方形草坪面积比原来面积小了,比原来少平方米,即相差平方米.
25.【答案】(1)解:原式=1+4-27=-22.
(2)解:原式=982-(98-1)(98+1)=982-982+1=1.
26.【答案】 解:
设这个两个数的十位上的数字是x,则这两个两位数是(10x+6)和(10x+4),
由题意得:(10x+6)2-(10x+4)2=220
解这个方程得:x=5
答:这两个两位数分别是:56和54.
27.【答案】解:∵9(x﹣1)2﹣2x﹣5=9x2﹣20x+4,
又∵个单项式加上9(x﹣1)2﹣2x﹣5后等于一个整式的平方,
∴此单项式可能是常数项,可能是一次项,可能是二次项,
①∵9x2﹣20x+4+=(3x﹣)2 , 故此单项式是;
②∵9x2﹣20x+4+8x=(3x﹣2)2 , 故此单项式是8x;
∵9x2﹣20x+4+32x=(3x+2)2 , 故此单项式是32x;
③∵9x2﹣20x+4+16x2=(5x﹣2)2 , 故此单项式是16x2;
故答案是、8x、32x、16x2 .
28.【答案】解:(1)1232﹣124×122??
=1232﹣(123+1)(123﹣1)
=1232﹣(1232﹣1)
=1232﹣1232+1?????
=1;
(2)(2a+b)(4a2+b2)(2a﹣b)
=(2a+b)(2a﹣b)(4a2+b2)
=(4a2﹣b2)(4a2+b2)
=(4a2)2﹣(b2)2
=16a4﹣b4 .
29.【答案】(1)a2﹣b2
(2)(a+b)(a﹣b)
(3)解:原式=(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+),
=××××…××××,
=.
试卷第4页,总4页
一、填空题(共10题;共30分)
1.计算:(2a+b)(2a-b)- =________.
2.计算:(x+1)2﹣(x+2)(x﹣2)=________.
3.两个正方形的边长和为20cm,它们的面积的差为40cm2 , 则这两个正方形的边长差为________ cm
4.若a+b=﹣3,ab=2,则a2+b2=________?
5. 已知,,则值为________.
6.(﹣x﹣11y)( ________?)=﹣121y2 .
7.化简:(m+n)(m﹣n)+2n2=________?
8.利用简便方法计算: =________.
9.计算:(x+4)(x﹣4)=________
10.在2001、2002、…、2010这10个数中,不能表示成两个平方数差的数有________个。
二、单选题(共10题;共30分)
11.下列各式能用平方差公式计算的是( ??)
A.?(2a+b)(2b-a)???????????????B.?(- x+1)(- x-1)???????????????C.?(a+b)(a-2b)???????????????D.?(2x-1)(-2x+1)
12.下列各式中不能用平方差公式计算的是(??? )
A.?(x-2y)(2y+x)???????????????B.?(x-2y)(-2y+x)???????????????C.?(x+y)(y-x)???????????????D.?(2x-3y)(3y+2x)
13.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图(1),然后拼成一个梯形,如图(2),根据这两个图形的面积关系,表明下列式子成立的是( )
A.?a2﹣b2=(a+b)(a﹣b)????????????????????????????????B.?(a+b)2=a2+2ab+b2
C.?(a﹣b)2=a2﹣2ab+b2???????????????????????????????????D.?a2﹣b2=(a﹣b)2
14.下列各式中,不能用平方差公式计算的是(?? )
A.?(﹣4x+3y)(4x+3y)????????????????????????????????????B.?(4x﹣3y)(3y﹣4x)??
C.?(﹣4x+3y)(﹣4x﹣3y)????????????????????????????????D.?(4x+3y)(4x﹣3y)
15.下列计算正确的一项是(?? )
A.?a5+a5=2a10???????????B.?(a+2)(a﹣2)=a2﹣4???????????C.?(a﹣b)2=a2﹣b2???????????D.?4a﹣2a=2
16.计算(a﹣b)(a+b)(a2+b2)(a4﹣b4)的结果是( )
A.?a8+2a4b4+b8???????????????????????B.?a8﹣2a4b4+b8???????????????????????C.?a8+b8???????????????????????D.?a8﹣b8
17. 下列算式能用平方差公式计算的是( )
A. B.
C. D.
18.下列乘法中,不能运用平方差公式进行运算的是( )
A.?(x+a)(x﹣a)???????????????????????????????????????????????B.?(﹣x﹣b)(x﹣b)
C.?(a+b)(﹣a﹣b)??????????????????????????????????????????D.?(b+m)(m﹣b)
19.计算(x﹣1)(﹣x﹣1)的结果是(?? )
A.?﹣x2+1????????????????????????????????B.?x2﹣1????????????????????????????????C.?﹣x2﹣1????????????????????????????????D.?x2+1
20.下列各式能用平方差公式计算的是( ??)???????
A.?(x+1)(x-1)????????B.?(a+b)(a-2b)????????C.?(-a+b)(a-b)????????D.?(-m-n)(m+n)
三、解答题(共9题;共60分)
21.先化简,再求值:(2x+1)(2x﹣1)﹣3x(x+1)﹣(x﹣1)2 , 当x=﹣1.
22.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”,如:4=22﹣02 , 12=42﹣22 , 20=62﹣42 , 因此4、12、20都是这种“神秘数”.
(1)28和2012这两个数是“神秘数”吗?试说明理由;
(2)试说明神秘数能被4整除;
(3)两个连续奇数的平方差是神秘数吗?试说明理由.
23.乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是________? (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是________?,长是________?,面积是________?.(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式________?.(用式子表达)
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
24. 有一块边长为米的正方形草坪,现南北各增长米,东西各缩短米,问所得长方形草坪面积比原来面积大,还是小,相差多少?
25.计算:
(1)计算:(﹣2016)0+( )﹣2+(﹣3)3;
(2)简算:982 -97×99.
26.两个两位数的十位上的数字相同,其中一个两位数的个位上的数字是6,另一个两位数的个位上的数字是4,它们的平方差是220,求这两位数..
27.一个单项式加上多项式9(x﹣1)2﹣2x﹣5后等于一个整式的平方,试求所有这样的单项式.
28.怎样简便就怎样计算:
(1)1232﹣124×122??????????????????????????
(2)(2a+b)(4a2+b2)(2a﹣b)
29.乘法公式的探究及应用:
(1)如图1所示,可以求出阴影部分面积是________?;(写成两数平方差的形式)
(2)若将图1中的阴影部分裁剪下来,重新拼成一个如图2的矩形,此矩形的面积是________?;(写成多项式乘法的形式)
(3)根据两图的阴影部分面积得到的乘法公式计算下列算式:
答案
一、填空题
1.【答案】3 +2ab-2
2.【答案】2x+5
3.【答案】2
4.【答案】5
5.【答案】±12
6.【答案】﹣x+11y
7.【答案】m2+n2
8.【答案】
9.【答案】x2﹣16
10.【答案】3
二、单选题
11.【答案】 B
12.【答案】 B
13.【答案】A
14.【答案】 B
15.【答案】B
16.【答案】 B
17.【答案】 D
18.【答案】C
19.【答案】 A
20.【答案】 A
三、解答题
21.【答案】解:原式=4x2﹣1﹣3x2﹣3x﹣x2+2x﹣1=﹣x﹣2,
当x=﹣1时,原式=1﹣2=﹣1.
22.【答案】解:(1)是,理由如下:
∵28=82﹣62 , 2012=5042﹣5022 ,
∴28是“神秘数”;2012是“神秘数”;
(2)“神秘数”是4的倍数.理由如下:
(2k+2)2﹣(2k)2=(2k+2+2k)(2k+2﹣2k)=2(4k+2)=4(2k+1),
∴“神秘数”是4的倍数;
(3)设两个连续的奇数为:2k+1,2k﹣1,则
(2k+1)2﹣(2k﹣1)2=8k,
而由(2)知“神秘数”是4的倍数,但不是8的倍数,
所以两个连续的奇数的平方差不是神秘数.
23.【答案】(1)a2﹣b2
(2)a﹣b;a+b;(a+b)(a﹣b)
(3)(a+b)(a﹣b)=a2﹣b2
(4)解:①原式=(10+0.3)×(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91;
②原式=[2m+(n﹣p)]?[2m﹣(n﹣p)]
=(2m)2﹣(n﹣p)2
=4m2﹣n2+2np﹣p2 .
24.【答案】解:根据题意得:
.
即所得长方形草坪面积比原来面积小了,比原来少平方米,即相差平方米.
25.【答案】(1)解:原式=1+4-27=-22.
(2)解:原式=982-(98-1)(98+1)=982-982+1=1.
26.【答案】 解:
设这个两个数的十位上的数字是x,则这两个两位数是(10x+6)和(10x+4),
由题意得:(10x+6)2-(10x+4)2=220
解这个方程得:x=5
答:这两个两位数分别是:56和54.
27.【答案】解:∵9(x﹣1)2﹣2x﹣5=9x2﹣20x+4,
又∵个单项式加上9(x﹣1)2﹣2x﹣5后等于一个整式的平方,
∴此单项式可能是常数项,可能是一次项,可能是二次项,
①∵9x2﹣20x+4+=(3x﹣)2 , 故此单项式是;
②∵9x2﹣20x+4+8x=(3x﹣2)2 , 故此单项式是8x;
∵9x2﹣20x+4+32x=(3x+2)2 , 故此单项式是32x;
③∵9x2﹣20x+4+16x2=(5x﹣2)2 , 故此单项式是16x2;
故答案是、8x、32x、16x2 .
28.【答案】解:(1)1232﹣124×122??
=1232﹣(123+1)(123﹣1)
=1232﹣(1232﹣1)
=1232﹣1232+1?????
=1;
(2)(2a+b)(4a2+b2)(2a﹣b)
=(2a+b)(2a﹣b)(4a2+b2)
=(4a2﹣b2)(4a2+b2)
=(4a2)2﹣(b2)2
=16a4﹣b4 .
29.【答案】(1)a2﹣b2
(2)(a+b)(a﹣b)
(3)解:原式=(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+),
=××××…××××,
=.
试卷第4页,总4页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
