沪科版九年级下册 24.1《旋转》图形的旋转课件 (25张PPT)
文档属性
| 名称 | 沪科版九年级下册 24.1《旋转》图形的旋转课件 (25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 362.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 00:00:00 | ||
图片预览




文档简介
课件25张PPT。图形的旋转扇叶水轮动感的旋转世界使用扳手拧螺丝活动1观 察、感知
1:上面情景中的转动现象,有什么共同的特征?
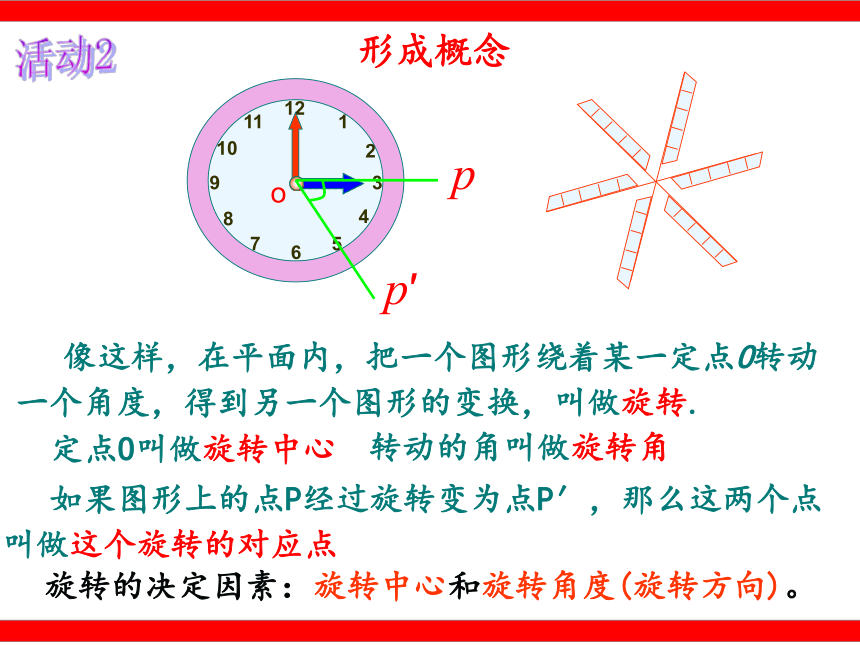
2:在转动过程中,其形状、大小、位置是否发生变化呢?探究: 像这样,在平面内,把一个图形绕着某一定点O转动一个角度,得到另一个图形的变换,叫做旋转. 定点O叫做旋转中心 如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点opp′转动的角叫做旋转角活动2形成概念 旋转的决定因素:旋转中心和旋转角度(旋转方向)。 1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5 抢答:2.下列物体的运动不是旋转的是( )
A.坐在摩天轮里的小朋友 B.正在走动的时针
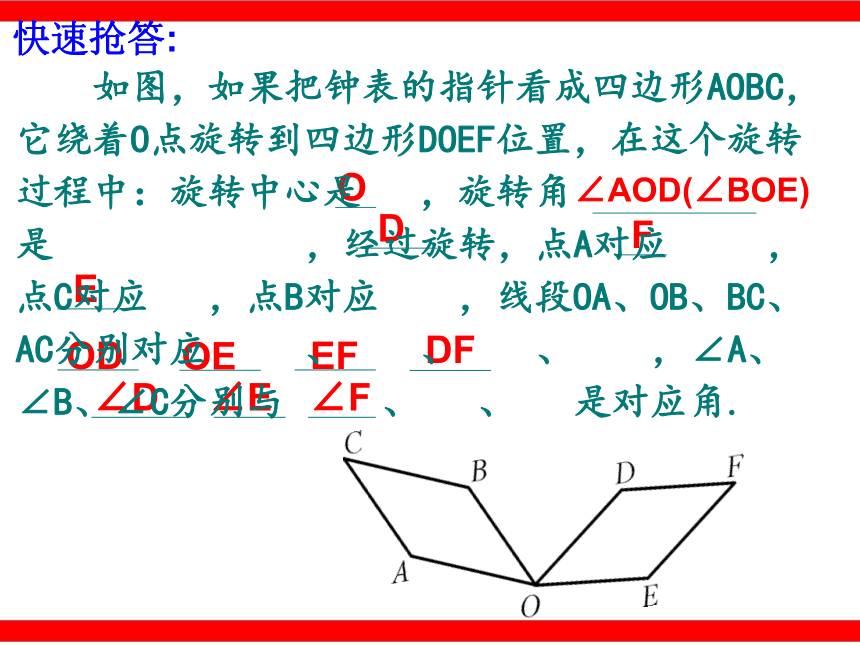
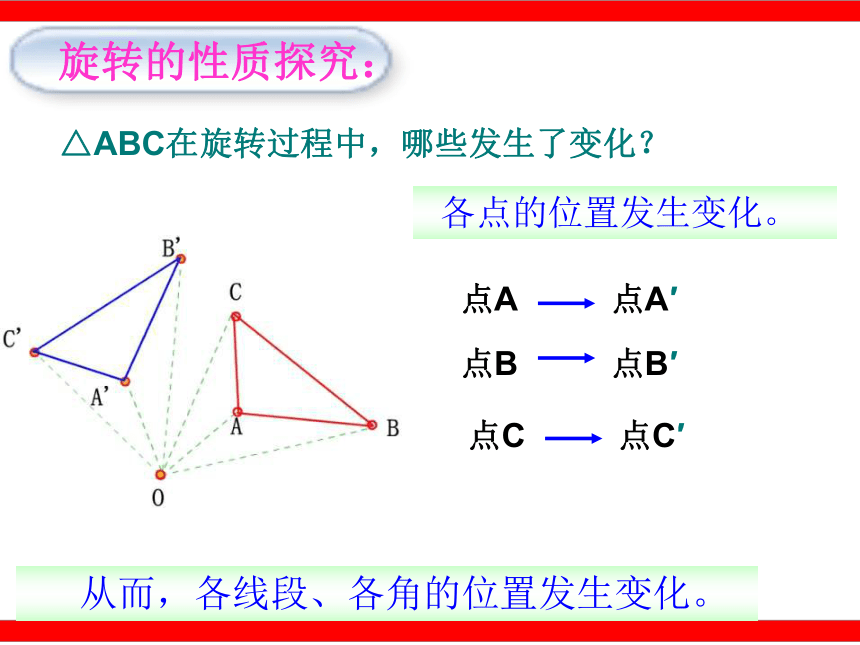
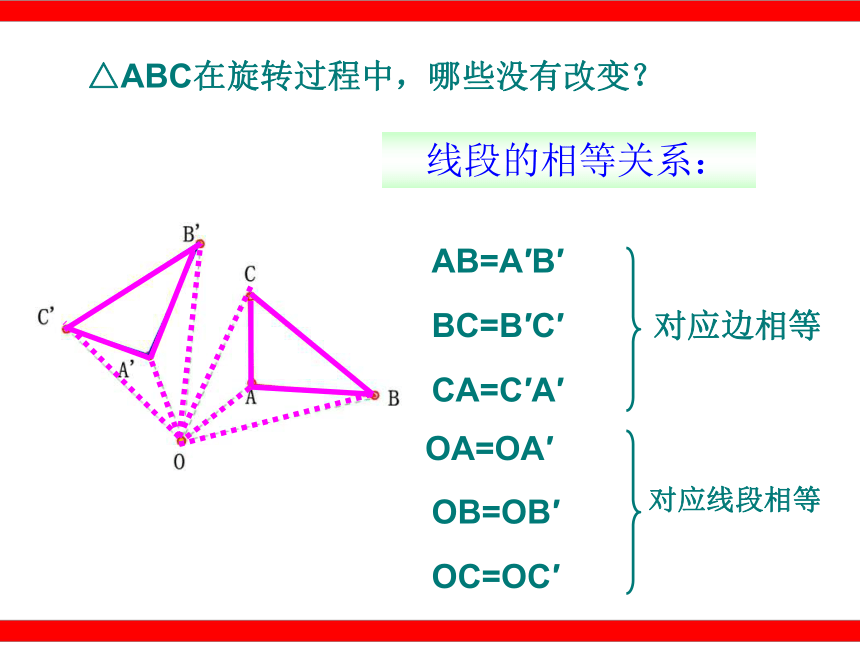
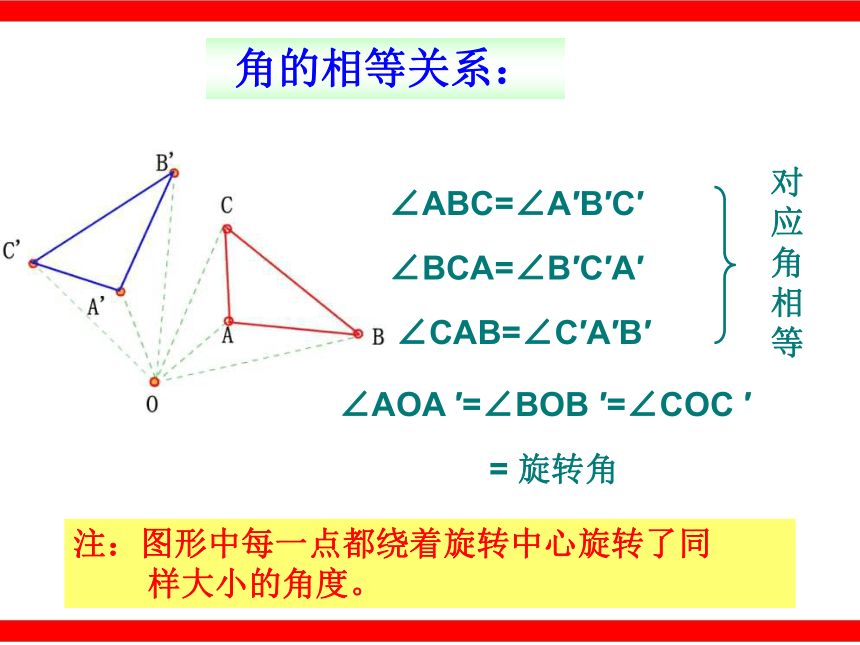
C.骑自行车的人 D.正在转动的风车叶片 C C快速抢答:∠AOD(∠BOE)ODFEODOEEFDF∠D∠E∠F 如图,如果把钟表的指针看成四边形AOBC,它绕着O点旋转到四边形DOEF位置,在这个旋转过程中:旋转中心是 ,旋转角是 ,经过旋转,点A对应 ,点C对应 ,点B对应 ,线段OA、OB、BC、AC分别对应 、 、 、 ,∠A、∠B、∠C分别与 、 、 是对应角. △ABC在旋转过程中,哪些发生了变化?旋转的性质探究: 各点的位置发生变化。点A′点A点B′点B点C′点C 从而,各线段、各角的位置发生变化。OA=OA′OB=OB′OC=OC′ 线段的相等关系:AB=A′B′BC=B′C′CA=C′A′对应边相等 △ABC在旋转过程中,哪些没有改变?对应线段相等 角的相等关系:∠ABC=∠A′B′C′ ∠AOA ′=∠BOB ′=∠COC ′ ∠BCA=∠B′C′A′ ∠CAB=∠C′A′B′ 对应角相等= 旋转角注:图形中每一点都绕着旋转中心旋转了同
样大小的角度。1. 对应点到旋转中心的距离相等。
2.对应点与旋转中心所连线段的夹角等于旋转角。
3.旋转前、后的图形全等。
即:对应边相等,对应 角相等。
4.图形的旋转不改变图形的形状、大小,只改变图形的位置。知识归纳:旋转的基本性质: 例1:四边形ABCD是正方形,△ABF是△ADE的旋转图形。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果连结EF,那么△AEF是怎样的三角形?点A (2)∵ △ABF是由△ADE旋转而得的,
∴ B是D的对应点。
∴ ∠DAB是旋转角,答:∴ ∠DAB = 90°,即旋转了90°。(3)等腰直角三角形 例2:如图,?ABC是等边三角形,D是BC上一点, ?ABD经过 旋转后到达?ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
AA点600如图所示:正方形ABCD中E为BC的中点,将△ABE旋转后得到△CBF.则旋转中心是__;
旋转角=___;AE与CF的位置关系_______ ;
如果正方形的面积为18cm2,△BCF的面积为4cm2,则四边形AECD的面积是_______B900互相垂直14cm2初试锋芒:ABCDD` 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将⊿ABD绕点A按逆时针方向旋转到⊿ACD`的位置,则∠ADD′=( )
A. 45° B . 48° C .30° D.60°A初试锋芒:如图所示,在△ABC中,∠BAC=90°,AB=AC,点P是△ABC内的一点,且AP=3,将△ABP绕点A旋转后与△ACP′重合,求PP′的长.解:依题意,AP绕点A旋转90°时得AP′=AP=3,则△APP′是等腰直角三角形.
所以PP′=
= = .挑战自我: 本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 18002次 1200 , 2400 5次 600, 1200, 1800, 2400, 3000
3个 1次 600火眼金睛: 像这样,在平面内,一个图形绕着一个定点旋转一定的角度后,能够与原图形重合,这样的图形叫旋转对称图形。这个定点就是旋转中心。 你还能举出其他旋转对称图形的例子吗?试试看!像,平行四边形,圆,线段,正多边形等。课堂回顾:这节课,主要学习了什么? 在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转旋转的概念:旋转的性质:1、旋转不改变图形的大小和形状.2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.3、对应点到旋转中心的距离相等作业:课后习题初试锋芒: 如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF=_____cm ,∠EBF=______39001.如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A.100 B.150 C.200 D.250
2、如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为 . B锋芒毕露:以 下 备 用ABCD 1. 如图,把正方形ABCD绕点A按顺时针方向旋转,得到正方形AEFG,边FG与BC交于点H,线段HG与HB相等吗?说明你的理由。EHGF相等,HL.挑战自我: 2.如图所示,点C是线段AB上任意一点,分别以AC、BC为边在同侧作等边三角形ACD和等边三角形BCE,连接AE、BD,试找出图中能通过旋转完全重合的一对三角形,并指明旋转中心、旋转角及旋转方向.解:△ACE旋转后能与△DCB完全重合.
旋转中心是点C,旋转角是60°,旋转方向是顺时针方向.(也可看作△DCB绕点C逆时针旋转60°得到△ACE)挑战自我: 挑战自我: 3 . 两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为,现把其中一个正方形固定不动,另一个正方形绕其中心旋转,问在旋转过程中,两个正方形重叠部分面积是否发生变化?说明理由.点拨精讲:设任转一角度,如图中的虚线部分,要说明旋转后正方形重叠部分面积不变,只要说明S△OEE′=S△ODD′,那么只要说明△OEF′≌△ODD′.? 勇攀高峰: (1)旋转中心是哪一点?(2)旋转角是多少度? 如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:ABFCEGDH(3)∠EAF等于多少度?(4)经过旋转,点B与点E分别转到
什么位置?(5)若点G是线段BE的中点,经过旋转
后,点G转到了什么位置?请在图形
上作出.
1:上面情景中的转动现象,有什么共同的特征?
2:在转动过程中,其形状、大小、位置是否发生变化呢?探究: 像这样,在平面内,把一个图形绕着某一定点O转动一个角度,得到另一个图形的变换,叫做旋转. 定点O叫做旋转中心 如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点opp′转动的角叫做旋转角活动2形成概念 旋转的决定因素:旋转中心和旋转角度(旋转方向)。 1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5 抢答:2.下列物体的运动不是旋转的是( )
A.坐在摩天轮里的小朋友 B.正在走动的时针
C.骑自行车的人 D.正在转动的风车叶片 C C快速抢答:∠AOD(∠BOE)ODFEODOEEFDF∠D∠E∠F 如图,如果把钟表的指针看成四边形AOBC,它绕着O点旋转到四边形DOEF位置,在这个旋转过程中:旋转中心是 ,旋转角是 ,经过旋转,点A对应 ,点C对应 ,点B对应 ,线段OA、OB、BC、AC分别对应 、 、 、 ,∠A、∠B、∠C分别与 、 、 是对应角. △ABC在旋转过程中,哪些发生了变化?旋转的性质探究: 各点的位置发生变化。点A′点A点B′点B点C′点C 从而,各线段、各角的位置发生变化。OA=OA′OB=OB′OC=OC′ 线段的相等关系:AB=A′B′BC=B′C′CA=C′A′对应边相等 △ABC在旋转过程中,哪些没有改变?对应线段相等 角的相等关系:∠ABC=∠A′B′C′ ∠AOA ′=∠BOB ′=∠COC ′ ∠BCA=∠B′C′A′ ∠CAB=∠C′A′B′ 对应角相等= 旋转角注:图形中每一点都绕着旋转中心旋转了同
样大小的角度。1. 对应点到旋转中心的距离相等。
2.对应点与旋转中心所连线段的夹角等于旋转角。
3.旋转前、后的图形全等。
即:对应边相等,对应 角相等。
4.图形的旋转不改变图形的形状、大小,只改变图形的位置。知识归纳:旋转的基本性质: 例1:四边形ABCD是正方形,△ABF是△ADE的旋转图形。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果连结EF,那么△AEF是怎样的三角形?点A (2)∵ △ABF是由△ADE旋转而得的,
∴ B是D的对应点。
∴ ∠DAB是旋转角,答:∴ ∠DAB = 90°,即旋转了90°。(3)等腰直角三角形 例2:如图,?ABC是等边三角形,D是BC上一点, ?ABD经过 旋转后到达?ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
AA点600如图所示:正方形ABCD中E为BC的中点,将△ABE旋转后得到△CBF.则旋转中心是__;
旋转角=___;AE与CF的位置关系_______ ;
如果正方形的面积为18cm2,△BCF的面积为4cm2,则四边形AECD的面积是_______B900互相垂直14cm2初试锋芒:ABCDD` 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将⊿ABD绕点A按逆时针方向旋转到⊿ACD`的位置,则∠ADD′=( )
A. 45° B . 48° C .30° D.60°A初试锋芒:如图所示,在△ABC中,∠BAC=90°,AB=AC,点P是△ABC内的一点,且AP=3,将△ABP绕点A旋转后与△ACP′重合,求PP′的长.解:依题意,AP绕点A旋转90°时得AP′=AP=3,则△APP′是等腰直角三角形.
所以PP′=
= = .挑战自我: 本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 18002次 1200 , 2400 5次 600, 1200, 1800, 2400, 3000
3个 1次 600火眼金睛: 像这样,在平面内,一个图形绕着一个定点旋转一定的角度后,能够与原图形重合,这样的图形叫旋转对称图形。这个定点就是旋转中心。 你还能举出其他旋转对称图形的例子吗?试试看!像,平行四边形,圆,线段,正多边形等。课堂回顾:这节课,主要学习了什么? 在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转旋转的概念:旋转的性质:1、旋转不改变图形的大小和形状.2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.3、对应点到旋转中心的距离相等作业:课后习题初试锋芒: 如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF=_____cm ,∠EBF=______39001.如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A.100 B.150 C.200 D.250
2、如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为 . B锋芒毕露:以 下 备 用ABCD 1. 如图,把正方形ABCD绕点A按顺时针方向旋转,得到正方形AEFG,边FG与BC交于点H,线段HG与HB相等吗?说明你的理由。EHGF相等,HL.挑战自我: 2.如图所示,点C是线段AB上任意一点,分别以AC、BC为边在同侧作等边三角形ACD和等边三角形BCE,连接AE、BD,试找出图中能通过旋转完全重合的一对三角形,并指明旋转中心、旋转角及旋转方向.解:△ACE旋转后能与△DCB完全重合.
旋转中心是点C,旋转角是60°,旋转方向是顺时针方向.(也可看作△DCB绕点C逆时针旋转60°得到△ACE)挑战自我: 挑战自我: 3 . 两个边长为1的正方形,如图所示,让一个正方形的顶点与另一个正方形中心重合,不难知道重合部分的面积为,现把其中一个正方形固定不动,另一个正方形绕其中心旋转,问在旋转过程中,两个正方形重叠部分面积是否发生变化?说明理由.点拨精讲:设任转一角度,如图中的虚线部分,要说明旋转后正方形重叠部分面积不变,只要说明S△OEE′=S△ODD′,那么只要说明△OEF′≌△ODD′.? 勇攀高峰: (1)旋转中心是哪一点?(2)旋转角是多少度? 如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:ABFCEGDH(3)∠EAF等于多少度?(4)经过旋转,点B与点E分别转到
什么位置?(5)若点G是线段BE的中点,经过旋转
后,点G转到了什么位置?请在图形
上作出.
