人教高中数学 (A版)必修五 1.1.2余弦定理教学设计
文档属性
| 名称 | 人教高中数学 (A版)必修五 1.1.2余弦定理教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 262.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 11:02:22 | ||
图片预览

文档简介
余弦定理教学设计
一、教学目标:
(1)由已有的知识直角三角形、正弦定理进一步研究三角形中其他的边角关系。
(2)学生合作探究通过直角三角形等已有知识,经历余弦定理的证明过程。
(3)注重公式结构及变形,掌握公式的内在联系
(4)公式的顺用与逆用
二、教学重点:余弦定理的发现及证明过程
教学难点:余弦定理的发现及证明
三、信息化设备:电子白板,录播室,几何画板
四、教学过程
知识回顾; :
(1)在一个三角形中各边和它的对边的正弦比相等,即:
(2) 运用正弦定理可以解决一些怎样的解三角形问题呢?
由,可以解决“已知两角及其一边可以求其他边。”“已知两边及其一边的对角可以求其他角。”等解三角形问题
余弦定理的教学过程:
1) 创设情境,激发学生兴趣
我们已经解决了两边及一边对角,以及两角一边解三角形----------正弦定理。
问题1:思考:如图,在中,已知,求c即。我们发现用正弦定理已无法解决这个问题,这就需要我们继续研究三角形中其他的边角关系。
问题2:我们研究问题的途径是什么?(由特殊到一般)
问题3:怎样把一般三角形化为特殊三角形呢?(分割、辅助线化为直角三角形)
问题:4、怎样表示出三角形的边c呢?
让学生遇到问题,激发兴趣,尝试解决
2) 余弦定理的得出及推导:
先让学生尝试具体问题:①已知三角形ABC中,a=5,b=1,C=,求第三边c
进而,改为字母:②已知三角形ABC中,BC=a,AC=b,∠ACB=C,试用a,b及C表示第三边c
设想:学生可能把图形加以分割转化为已有知识直角三角形进行解决。
小组合作探讨:
证明:学生可能想法有
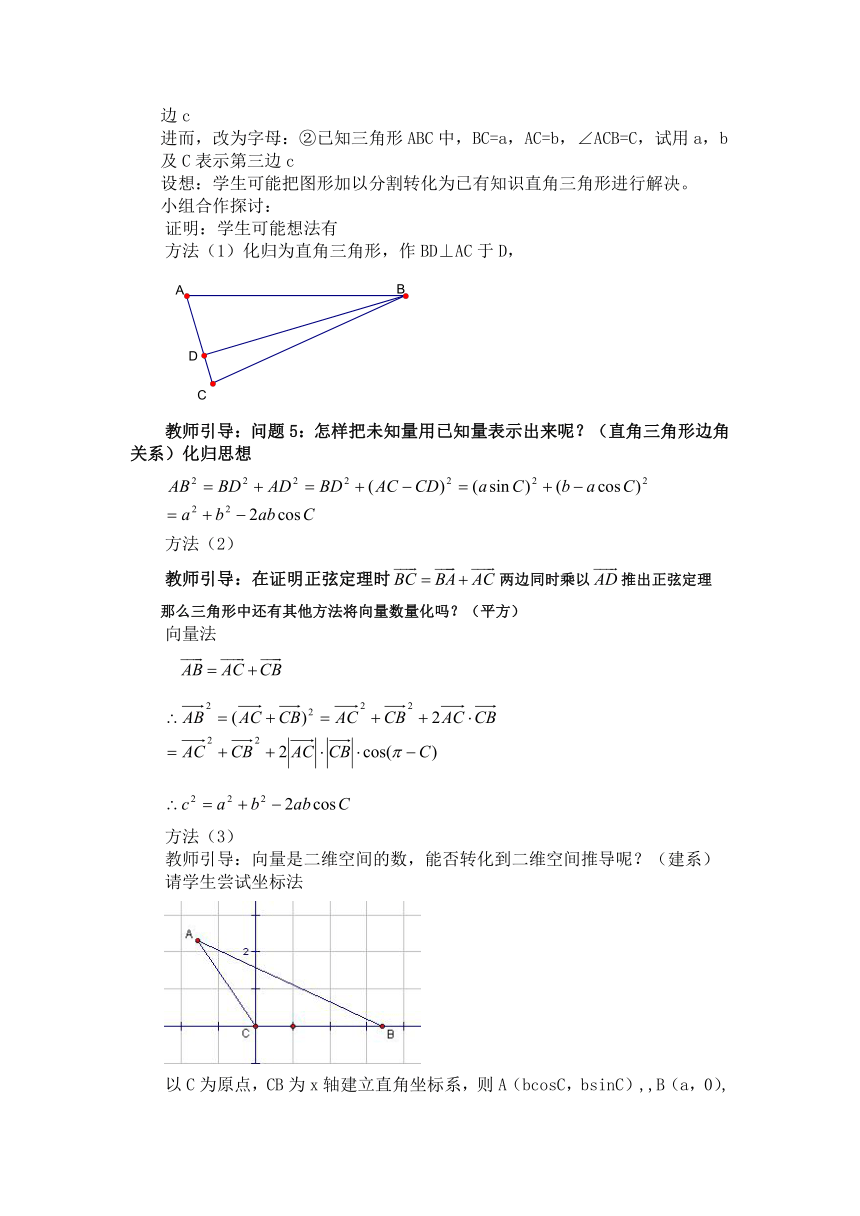
方法(1)化归为直角三角形,作BD⊥AC于D,
教师引导:问题5:怎样把未知量用已知量表示出来呢?(直角三角形边角关系)化归思想
方法(2)
教师引导:在证明正弦定理时两边同时乘以推出正弦定理
那么三角形中还有其他方法将向量数量化吗?(平方)
向量法
方法(3)
教师引导:向量是二维空间的数,能否转化到二维空间推导呢?(建系)
请学生尝试坐标法
以C为原点,CB为x轴建立直角坐标系,则A(bcosC,bsinC),,B(a,0),
同理可得,,
教师可以借助用几何画板形象直观的反映出数量关系。
(几何画板供参考)
利用几何画板制作动画,帮助学生认知:
公式变形:,,
问题6我们怎样记忆公式:结构的对称性,角和边的对应,我们观察一个等式是从整体到局部,由特殊到一般的过程,余弦定理就是勾股定理的推广。
(1)余弦定理与正弦定理一样,也是任何三角形边角之间存在的共同规律,余弦定理是勾股定理的推广,勾股定理是余弦定理的特例.
(2)等式含有四个量,从方程的角度看,已知其中三个量,总可以求出第四个量。
问题7:我们为什么要学余弦定理,他有什么用呢?
利用余弦定理及推论可以解决以下两类三角形的问题:
①已知三边求三角形的三个角;
②已知两边及其夹角求三角形的其他边与角。
这两种类型问题在有解时都只有一个解,把“边、边、边”和“边、角、边”判定三角形全等的定理从数量化的角度进行刻画,使其变成了可计算的公式。
(4)从余弦定理和余弦函数的性质可知:在一个三角形中,如果两边的平方和等于第三边的平方,那么第三边所对的角是直角;如果两边的平方和大于第三边的平方,那么第三边所对的角是锐角;如果两边的平方和小于第三边的平方,那么第三边所对的角是钝角;
余弦定理是勾股定理的推广,利用余弦定理可以解决以下两类问题:已知三边求三角;已知两边和夹角求第三边和其他各角
五、问题解决:
问题1:中,,解这个三角形。
解:∵,
∴这个三角形的最大角是。
所以这个三角形的最大角是。
引申:已知三角形三边长为,怎样判断是锐角三角形、直角三角形还是钝角三角形?
反馈练习:1、中,,求及。(学生板演、教师评讲,强调规范化解题)
六、归纳小结 反思拓展
(一)归纳小结
1、余弦定理是任何三角形边角之间存在的共同规律,余弦定理是勾股定理的推广,勾股定理是余弦定理的特例。能否用余弦定理证明勾股定理呢?
2、余弦定理有两个基本应用:一是已知三边求三角,二是已知两边及他们的夹角求第三边。
3、余弦定理和正弦定理是同一三角形的约束条件的不同表现形式,在本质上应该是一致的。
4、要让学生体会余弦定理的发现过程,尤其是怎么想到这个方法的。
(二)反思拓展、课后探讨
1、余弦定理和正弦定理反映了同一三角形边、角之间的的度量关系,本质上是一致的.你能证明这两个定理时等价的吗?
2、总结解三角形的方法:已知三角形边角中哪三个量,有唯一解或多解或无解?分别用什么方法?
作业; 1、P51 练习第1、2题;
2、课后探讨内容
一、教学目标:
(1)由已有的知识直角三角形、正弦定理进一步研究三角形中其他的边角关系。
(2)学生合作探究通过直角三角形等已有知识,经历余弦定理的证明过程。
(3)注重公式结构及变形,掌握公式的内在联系
(4)公式的顺用与逆用
二、教学重点:余弦定理的发现及证明过程
教学难点:余弦定理的发现及证明
三、信息化设备:电子白板,录播室,几何画板
四、教学过程
知识回顾; :
(1)在一个三角形中各边和它的对边的正弦比相等,即:
(2) 运用正弦定理可以解决一些怎样的解三角形问题呢?
由,可以解决“已知两角及其一边可以求其他边。”“已知两边及其一边的对角可以求其他角。”等解三角形问题
余弦定理的教学过程:
1) 创设情境,激发学生兴趣
我们已经解决了两边及一边对角,以及两角一边解三角形----------正弦定理。
问题1:思考:如图,在中,已知,求c即。我们发现用正弦定理已无法解决这个问题,这就需要我们继续研究三角形中其他的边角关系。
问题2:我们研究问题的途径是什么?(由特殊到一般)
问题3:怎样把一般三角形化为特殊三角形呢?(分割、辅助线化为直角三角形)
问题:4、怎样表示出三角形的边c呢?
让学生遇到问题,激发兴趣,尝试解决
2) 余弦定理的得出及推导:
先让学生尝试具体问题:①已知三角形ABC中,a=5,b=1,C=,求第三边c
进而,改为字母:②已知三角形ABC中,BC=a,AC=b,∠ACB=C,试用a,b及C表示第三边c
设想:学生可能把图形加以分割转化为已有知识直角三角形进行解决。
小组合作探讨:
证明:学生可能想法有
方法(1)化归为直角三角形,作BD⊥AC于D,
教师引导:问题5:怎样把未知量用已知量表示出来呢?(直角三角形边角关系)化归思想
方法(2)
教师引导:在证明正弦定理时两边同时乘以推出正弦定理
那么三角形中还有其他方法将向量数量化吗?(平方)
向量法
方法(3)
教师引导:向量是二维空间的数,能否转化到二维空间推导呢?(建系)
请学生尝试坐标法
以C为原点,CB为x轴建立直角坐标系,则A(bcosC,bsinC),,B(a,0),
同理可得,,
教师可以借助用几何画板形象直观的反映出数量关系。
(几何画板供参考)
利用几何画板制作动画,帮助学生认知:
公式变形:,,
问题6我们怎样记忆公式:结构的对称性,角和边的对应,我们观察一个等式是从整体到局部,由特殊到一般的过程,余弦定理就是勾股定理的推广。
(1)余弦定理与正弦定理一样,也是任何三角形边角之间存在的共同规律,余弦定理是勾股定理的推广,勾股定理是余弦定理的特例.
(2)等式含有四个量,从方程的角度看,已知其中三个量,总可以求出第四个量。
问题7:我们为什么要学余弦定理,他有什么用呢?
利用余弦定理及推论可以解决以下两类三角形的问题:
①已知三边求三角形的三个角;
②已知两边及其夹角求三角形的其他边与角。
这两种类型问题在有解时都只有一个解,把“边、边、边”和“边、角、边”判定三角形全等的定理从数量化的角度进行刻画,使其变成了可计算的公式。
(4)从余弦定理和余弦函数的性质可知:在一个三角形中,如果两边的平方和等于第三边的平方,那么第三边所对的角是直角;如果两边的平方和大于第三边的平方,那么第三边所对的角是锐角;如果两边的平方和小于第三边的平方,那么第三边所对的角是钝角;
余弦定理是勾股定理的推广,利用余弦定理可以解决以下两类问题:已知三边求三角;已知两边和夹角求第三边和其他各角
五、问题解决:
问题1:中,,解这个三角形。
解:∵,
∴这个三角形的最大角是。
所以这个三角形的最大角是。
引申:已知三角形三边长为,怎样判断是锐角三角形、直角三角形还是钝角三角形?
反馈练习:1、中,,求及。(学生板演、教师评讲,强调规范化解题)
六、归纳小结 反思拓展
(一)归纳小结
1、余弦定理是任何三角形边角之间存在的共同规律,余弦定理是勾股定理的推广,勾股定理是余弦定理的特例。能否用余弦定理证明勾股定理呢?
2、余弦定理有两个基本应用:一是已知三边求三角,二是已知两边及他们的夹角求第三边。
3、余弦定理和正弦定理是同一三角形的约束条件的不同表现形式,在本质上应该是一致的。
4、要让学生体会余弦定理的发现过程,尤其是怎么想到这个方法的。
(二)反思拓展、课后探讨
1、余弦定理和正弦定理反映了同一三角形边、角之间的的度量关系,本质上是一致的.你能证明这两个定理时等价的吗?
2、总结解三角形的方法:已知三角形边角中哪三个量,有唯一解或多解或无解?分别用什么方法?
作业; 1、P51 练习第1、2题;
2、课后探讨内容
