18.1.2 平行四边形的判定(2)课件
图片预览



文档简介
人教版数学八年级下册
18.1.2平行四边形的判定(2)
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
1、已知在四边形ABCD中,AD∥BC,要使这个四边形为平行四边形,则需添加一个你认为正确的条件为:
A B∥DC,或∠A =∠C或AD=BC
2、能判定一个四边形是平行四边形的条件是( )
A、一组对角相等 B、一组对边平行且相等
C、一对邻角互补 D、两条对角线互相垂直
B
3、四边形ABCD中,若∠A = ∠C,∠B = ∠D,则下列结论中错误的是( )
C
A、AB = CD B、AD∥BC
C、∠A = ∠B D、对角线互相平分
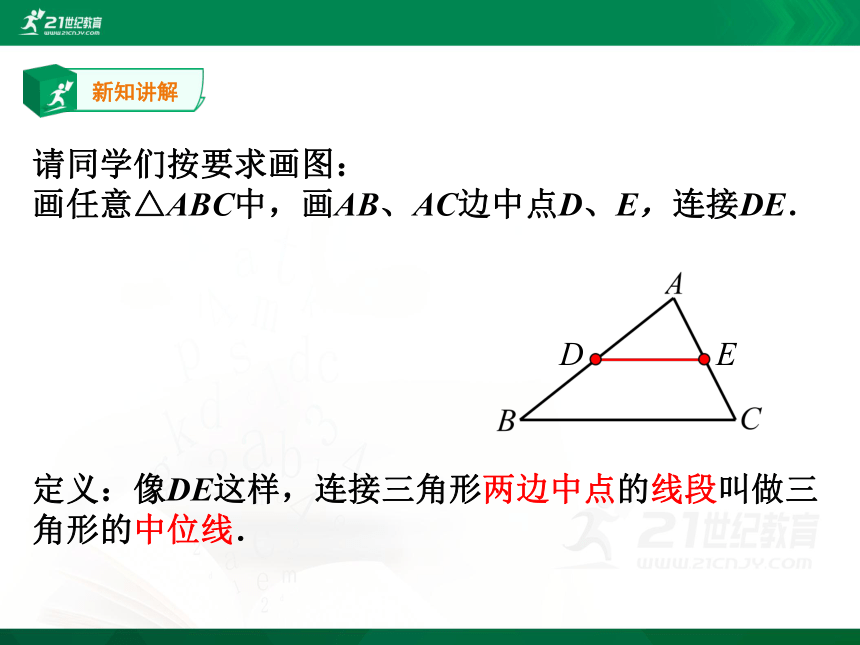
请同学们按要求画图:
画任意△ABC中,画AB、AC边中点D、E,连接DE.
定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
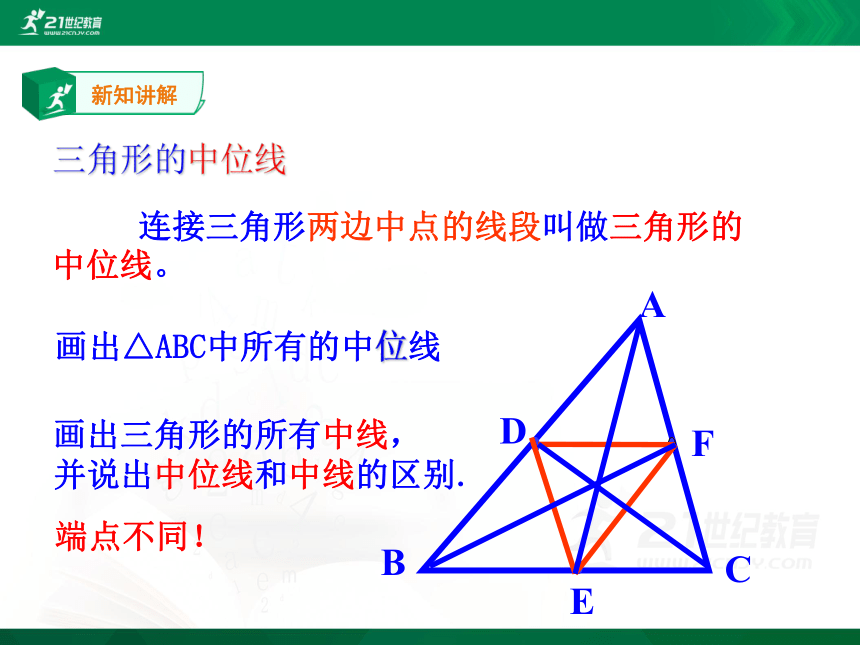
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
画出三角形的所有中线,
并说出中位线和中线的区别.
D
E
F
端点不同!
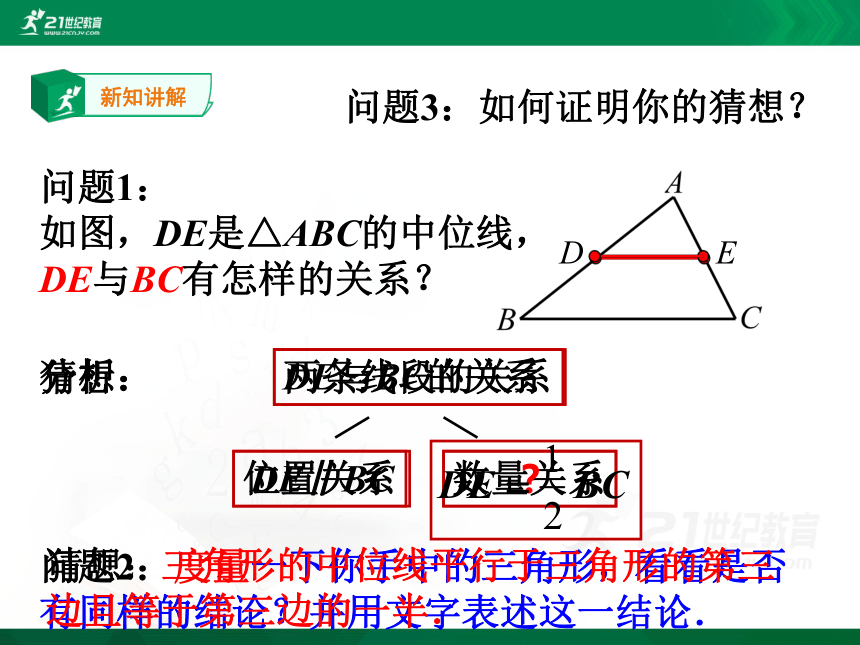
问题1:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
问题2:度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
猜想:三角形的中位线平行于三角形的第三边且等于第三边的一半.
问题3:如何证明你的猜想?Z```x``xk
F
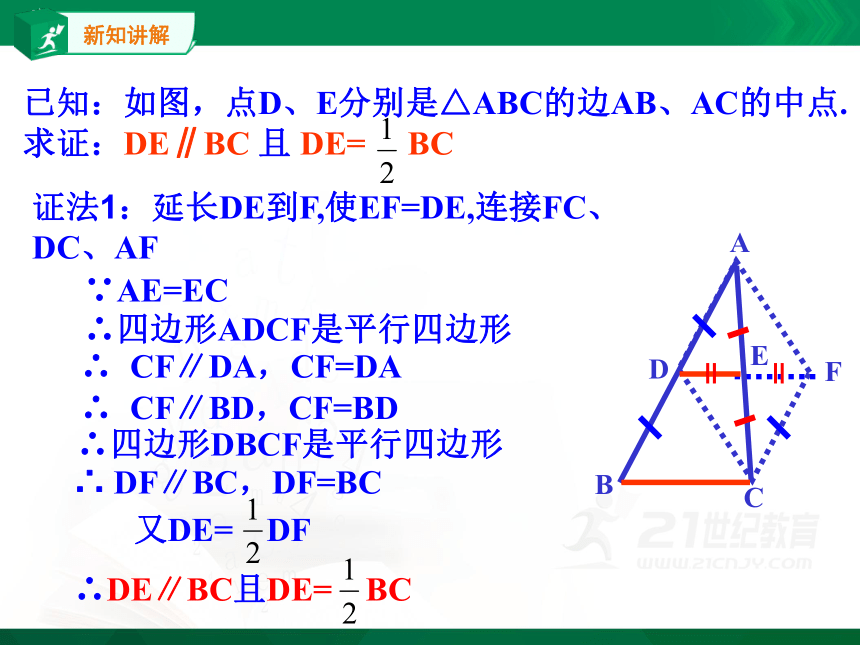
证法1:延长DE到F,使EF=DE,连接FC、
DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
∴ CF∥DA,CF=DA
∴ CF∥BD,CF=BD
∴ DF∥BC,DF=BC
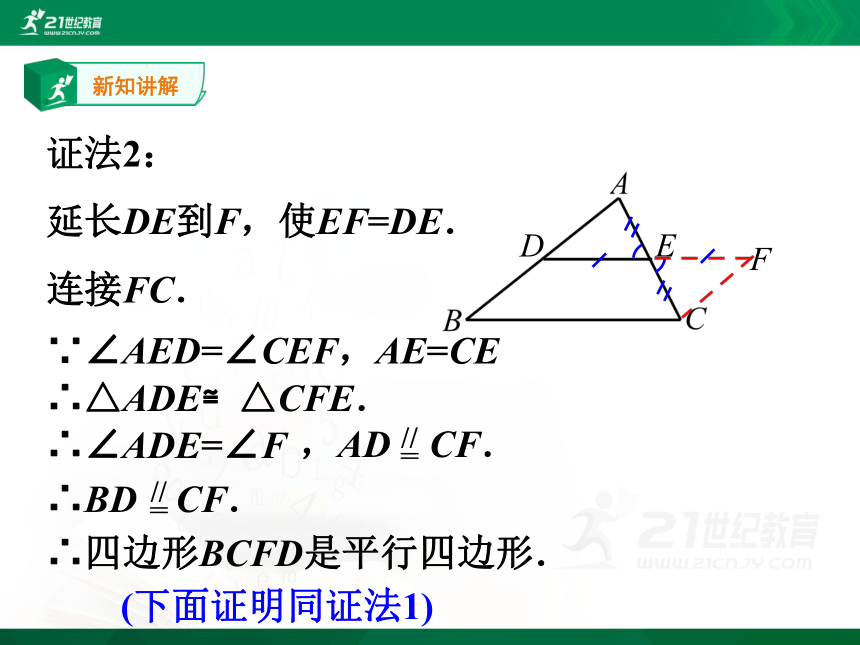
证法2:
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE
(下面证明同证法1)
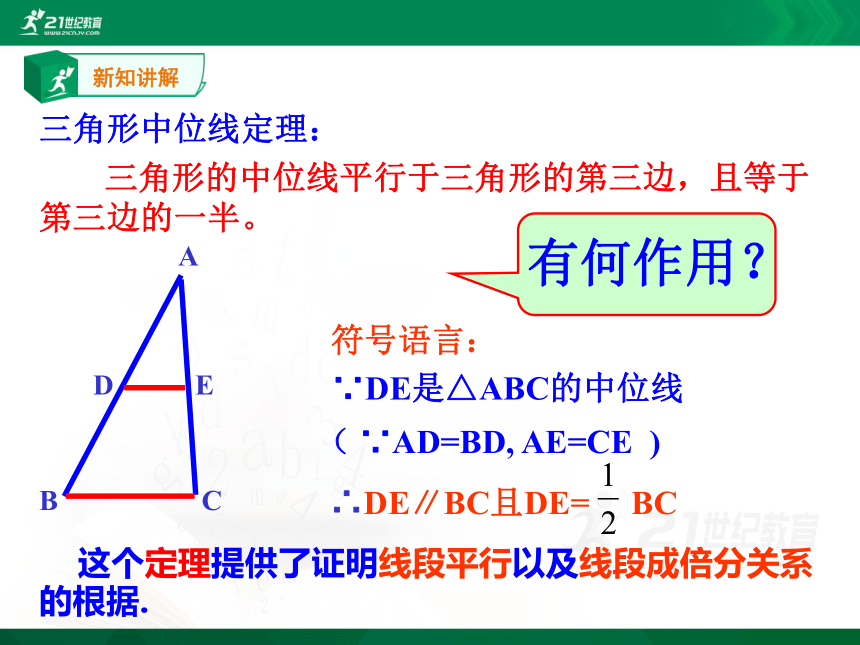
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
三角形中位线定理:
∵DE是△ABC的中位线
符号语言:
( ∵AD=BD, AE=CE )
这个定理提供了证明线段平行以及线段成倍分关系的根据.
G
F
E
D
O
∴四边形DGFE是平行四边形
证明:
例1:如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
求证:四边形DGFE是平行四边形.
典型例题
证明:
例2:如图,△ABC中,D是AB上一点,且 AD=AC , AE⊥CD于E,F是CB的中点。
求证:BD=2EF
6
15
例3:如图,□ABCD的周长为36,对角线AC、 BD交于点O, 点E是CD的中点,BD=12,求△DOE的周长.
例4 如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样量出A、B两点间的距离?根据是什么?
分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
N
M
根据是三角形中位线定理.
E
F
G
H
A
B
C
D
(一组对边平行且相等的四边形是平行四边形)
顺次连接四边形各边中点的线段组成一个平行四边形
例5:已知: 如图,点E、F、G、H分别是四边形 ABCD各边中点。
求证:四边形EFGH为平行四边形。
例6:如图,D、 E 、F分别是△ABC三边中点,AH⊥BC于H.
求证:DF=EH
A
B
C
H
F
E
D
例7:如图,△ABC中,M是BC的中点,AD是
∠ B AC的平分线 , BD⊥AD于D,AB=12,
AC=18. 求DM的长.
12
18
N
△ ADB ≌ △ ADN
6
3
例8:如图,在四边形ABCD中,对角线AC,BD相交于点O,且 ,E,F分别是AB,CD的中点,EF分别交BD,AC于点G , H。
求证:
H
G
O
F
E
AC=BD
OG=OH
M
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)
1. 如图,△ABC中,D、E分别是AB、AC中点.
(1) 若DE=5,则BC= .
(2) 若∠B=65°,则∠ADE= °.
(3) 若DE+BC=12,则BC= .
10
65
x
2x
8
2.已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△ABC的周长是12cm,那么△DEF的周长是?? ?? cm.
3.一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是?? ?cm.
6
270
4.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?
A
B
C
D
E
F
3个
证明:
取AE的中点F,连接DF
∵D是AB中点
∴DF是△ABE的中位线
∴DF=1/2BE且DF‖BE(三角形中位线定理)
∵3AE=2AC
∴AE=2/3AC
∴AF=FE=EC=1/3AC
在△CFD中,
∵?EF=EC且DF//BE,即OE//DF,?
∴?CO=DO(过三角形一边中点,与另一边平行的
直线,必平分第三边)?
∴?OE是△CDF的中位线?
∴?OE=1/2DF?
∴?OE=1/4BE。
必做题:教材第49页练习第1、2题.
选做题:顺次连接平行四边形各边中点,得到一个新的四边形,判断这个新四边形是否是平行四边形,并说明理由.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
18.1.2平行四边形的判定(2)
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
1、已知在四边形ABCD中,AD∥BC,要使这个四边形为平行四边形,则需添加一个你认为正确的条件为:
A B∥DC,或∠A =∠C或AD=BC
2、能判定一个四边形是平行四边形的条件是( )
A、一组对角相等 B、一组对边平行且相等
C、一对邻角互补 D、两条对角线互相垂直
B
3、四边形ABCD中,若∠A = ∠C,∠B = ∠D,则下列结论中错误的是( )
C
A、AB = CD B、AD∥BC
C、∠A = ∠B D、对角线互相平分
请同学们按要求画图:
画任意△ABC中,画AB、AC边中点D、E,连接DE.
定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
画出三角形的所有中线,
并说出中位线和中线的区别.
D
E
F
端点不同!
问题1:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
问题2:度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
猜想:三角形的中位线平行于三角形的第三边且等于第三边的一半.
问题3:如何证明你的猜想?Z```x``xk
F
证法1:延长DE到F,使EF=DE,连接FC、
DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
∴ CF∥DA,CF=DA
∴ CF∥BD,CF=BD
∴ DF∥BC,DF=BC
证法2:
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE
(下面证明同证法1)
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
三角形中位线定理:
∵DE是△ABC的中位线
符号语言:
( ∵AD=BD, AE=CE )
这个定理提供了证明线段平行以及线段成倍分关系的根据.
G
F
E
D
O
∴四边形DGFE是平行四边形
证明:
例1:如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
求证:四边形DGFE是平行四边形.
典型例题
证明:
例2:如图,△ABC中,D是AB上一点,且 AD=AC , AE⊥CD于E,F是CB的中点。
求证:BD=2EF
6
15
例3:如图,□ABCD的周长为36,对角线AC、 BD交于点O, 点E是CD的中点,BD=12,求△DOE的周长.
例4 如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样量出A、B两点间的距离?根据是什么?
分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
N
M
根据是三角形中位线定理.
E
F
G
H
A
B
C
D
(一组对边平行且相等的四边形是平行四边形)
顺次连接四边形各边中点的线段组成一个平行四边形
例5:已知: 如图,点E、F、G、H分别是四边形 ABCD各边中点。
求证:四边形EFGH为平行四边形。
例6:如图,D、 E 、F分别是△ABC三边中点,AH⊥BC于H.
求证:DF=EH
A
B
C
H
F
E
D
例7:如图,△ABC中,M是BC的中点,AD是
∠ B AC的平分线 , BD⊥AD于D,AB=12,
AC=18. 求DM的长.
12
18
N
△ ADB ≌ △ ADN
6
3
例8:如图,在四边形ABCD中,对角线AC,BD相交于点O,且 ,E,F分别是AB,CD的中点,EF分别交BD,AC于点G , H。
求证:
H
G
O
F
E
AC=BD
OG=OH
M
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)
1. 如图,△ABC中,D、E分别是AB、AC中点.
(1) 若DE=5,则BC= .
(2) 若∠B=65°,则∠ADE= °.
(3) 若DE+BC=12,则BC= .
10
65
x
2x
8
2.已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△ABC的周长是12cm,那么△DEF的周长是?? ?? cm.
3.一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是?? ?cm.
6
270
4.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?
A
B
C
D
E
F
3个
证明:
取AE的中点F,连接DF
∵D是AB中点
∴DF是△ABE的中位线
∴DF=1/2BE且DF‖BE(三角形中位线定理)
∵3AE=2AC
∴AE=2/3AC
∴AF=FE=EC=1/3AC
在△CFD中,
∵?EF=EC且DF//BE,即OE//DF,?
∴?CO=DO(过三角形一边中点,与另一边平行的
直线,必平分第三边)?
∴?OE是△CDF的中位线?
∴?OE=1/2DF?
∴?OE=1/4BE。
必做题:教材第49页练习第1、2题.
选做题:顺次连接平行四边形各边中点,得到一个新的四边形,判断这个新四边形是否是平行四边形,并说明理由.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
