2018-2019学年江苏省泰州市高二(上)期末数学试卷(文科)
文档属性
| 名称 | 2018-2019学年江苏省泰州市高二(上)期末数学试卷(文科) |  | |
| 格式 | zip | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 10:53:08 | ||
图片预览




文档简介
2018-2019学年江苏省泰州市高二(上)期末数学试卷(文科)
一、填空题(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上)
1.(5分)命题:“若a=0,则ab=0”的逆否命题是 .
2.(5分)已知复数z=2﹣i(i是虚数单位),则|z|= .
3.(5分)已知椭圆,则椭圆的焦点坐标是 .
4.(5分)“(x+2)(x﹣1)<0”是“﹣3<x<1”成立的 条件(在“充分不必要”,“必要不充分”,“充要”,“既不充分又不必要”中选一个填写).
5.(5分)函数f(x)=sinx﹣x,x∈(0,)的单调递增区间是 .
6.(5分)若双曲线C:(a>0,b>0)的离心率为,则的值为 .
7.(5分)直线l过点(0,1),且与曲线y=f(x)相切于点(a,3),若f'(a)=1,则实数a的值是 .
8.(5分)古埃及发现如下有趣等式:,,,,…,按此规律,= (n∈N*).
9.(5分)函数f(x)的定义域为R,若对任意的x∈R,f(x)+xf'(x)>0,且,则不等式(x2+1)f(x2+1)>1的解集为 .
10.(5分)在实数中:要证明实数a,b相等,可以利用a≤b且a≥b来证明:类比到集合中:要证明集合A,B相等,可以利用 来证明.
11.(5分)已知椭圆C:,过点P(0,6)的直线l与椭圆C交于A,B两点,若A是线段PB的中点,则点A的坐标为 .
12.(5分)若定义在R上的函数f(x)=|x3﹣3x2+m|有三个不同的单调递增区间,则实数m的取值范围是 .
13.(5分)已知椭圆C:的右焦点为F(2,0),F关于直线的对称点Q在椭圆C上,则b= .
14.(5分)若函数在(l,+∞)上的最大值为8,则实数a的值为 .
二、解答题(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤)
15.(14分)已知复数z=,(m∈R,i是虚数单位)
(1)若z是纯虚数,求m的值;
(2)设是z的共轭复数,在复平面上对应的点在第四象限,求m的取值范围.
16.(14分)已知p:函数f(x)=x2﹣2mx+1在(﹣∞,1)上单调递减(其中m∈R),q:?x∈R,x2+2x+m≥0(其中m∈R).
(1)如果“p且q”为真,求实数m的取值范围.
(2)如果“p或q”为真,“p且q”为假,求实数m的取值范围.
17.(14分)(1)已知f(x)=,x∈[0,+∞),若x1,x2∈[0,+∞),且x1≠x2,求证:[f(x1)+f(x2)]<f();
(2)用反证法证明:若f(x)为R上的增函数,且a+f(a)≤b+f(b),求证:a≤b.
18.(16分)如图,以两条互相垂直的公路所在直线分别为x轴,y轴建立平面直角坐标系,公路附近有一居民区EFG和一风景区,其中OE=1(单位:百米),∠OEF=45°,风景区的部分边界为曲线C,曲线C的方程为y=(≤x≤5),拟在居民和风景区间辟出一个三角形区域EMN用于工作人员办公,点M,N分别在x轴和EF上,且MN与曲线C相切于P点.
(1)设P点的横坐标为t,写出△EMN面积的函数表达式S(t);
(2)当t为何值时,△EMN面积最小?并求出最小面积.
19.(16分)在平面直角坐标系xOy中,已知椭圆C:的右准线方程为x=4,右顶点为A(2,0).
(1)求椭圆C的方程;
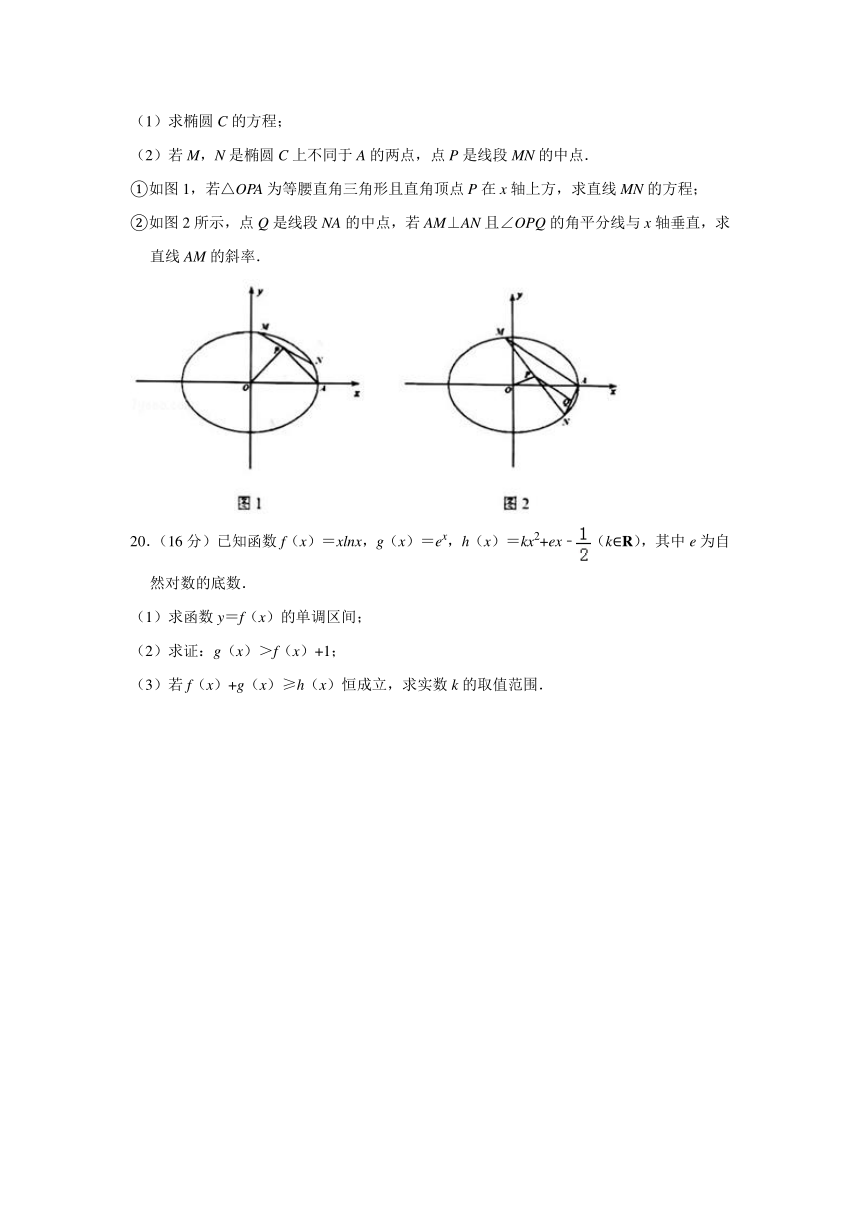
(2)若M,N是椭圆C上不同于A的两点,点P是线段MN的中点.
①如图1,若△OPA为等腰直角三角形且直角顶点P在x轴上方,求直线MN的方程;
②如图2所示,点Q是线段NA的中点,若AM⊥AN且∠OPQ的角平分线与x轴垂直,求直线AM的斜率.
20.(16分)已知函数f(x)=xlnx,g(x)=ex,h(x)=kx2+ex﹣(k∈R),其中e为自然对数的底数.
(1)求函数y=f(x)的单调区间;
(2)求证:g(x)>f(x)+1;
(3)若f(x)+g(x)≥h(x)恒成立,求实数k的取值范围.
2018-2019学年江苏省泰州市高二(上)期末数学试卷(文科)
参考答案与试题解析
一、填空题(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上)
1.【解答】解:∵:“若a=0,则ab=0”
∴逆否命题:若ab≠0,则a≠0
故答案为:若ab≠0,则a≠0
2.【解答】解:∵复数z=2﹣i,
∴|z|===.
故答案为:.
3.【解答】解:∵椭圆,∴a2=25,b2=16
∴c2=a2﹣b2=9
∴c=3
∴椭圆的焦点坐标是(﹣3,0),(3,0)
故答案为:(﹣3,0),(3,0)
4.【解答】解:(x+2)(x﹣1)<0,解得﹣2<x<1.
∴“(x+2)(x﹣1)<0”是“﹣3<x<1”成立的充分不必要条件.
故答案为:充分不必要.
5.【解答】解:由f(x)=sinx﹣x,x∈(0,),得f′(x)=cosx﹣,
由f′(x)=cosx﹣>0,得cosx>,
∵x∈(0,),∴x∈(0,),
则f(x)的单调递增区间为(0,).
故答案为:(0,).
6.【解答】解:双曲线C:(a>0,b>0)的离心率为,
可得e==,可得a2+b2=10a2,可得=3.
故答案为:3.
7.【解答】解:直线l经过点(0,1),且与曲线y=f(x)相切于点(a,3).若f′(a)=1,
切线的斜率为1,切线方程为:y﹣1=x,
所以3﹣1=a,解得a=2.
故答案为:2.
8.【解答】解:由,,,,…,可归纳出:=+,
故答案为:+,
9.【解答】解:令g(x)=xf(x),则g′(x)=f(x)+xf'(x)>0,
可得g(x)在(﹣∞,+∞)上为增函数,
由,得g(2)=2f(2)=1,
∴不等式(x2+1)f(x2+1)>1化为g(x2+1)>g(2),
又g(x)在(﹣∞,+∞)上为增函数,
∴x2+1>2,得x<﹣1或x>1.
∴不等式(x2+1)f(x2+1)>1的解集为(﹣∞,﹣1)∪(1,+∞).
故答案为:(﹣∞,﹣1)∪(1,+∞).
10.【解答】解:在实数中:要证明实数a,b相等,可以利用a≤b且a≥b来证明:类比到集合中:要证明集合A,B相等,可以利用 A?B且B?A来证明.
故答案为:A?B且B?A.
11.【解答】解:易知直线的斜率存在,设直线AB的方程y=kx+6,设A(x1,y1),B(x2,y2),
∵A是线段PB的中点,
∴2x1=x2,①
由,消y整理可得(3+4k2)x2+48kx+96=0,
∴x1+x2=﹣,②,x1x2=,③,
由①②③可得=,
整理解得4k2=9,
∴x12==4,
∴x1=±2,
∴y1=±3,
∴A(2,3)或(﹣2,3)
故答案为:(2,3)或(﹣2,3)
12.【解答】解:令g(x)=x3﹣3x2+m,由g′(x)=3x2﹣6x=0可得,x=0或x=2.
g(x)在(﹣∞,0),(2,+∞)递增,在(0,2)递减.
要使函数f(x)=|x3﹣3x2+m|有三个不同的单调递增区间,则g(x)的图象只能如下图所示,
∴∴0<m<4.
故答案为:(0,4).
13.【解答】解:设Q(m,n),
由F关于直线的对称点Q在椭圆C上,
∴?=﹣1,=?(),
解得m=,n=,
∵点Q在椭圆上,且a2=4+b2,
∴+=1,
整理可得b2(b2+4)2=256,
∴b(b2+4)=16,
解得b=2,
故答案为:2
14.【解答】解:函数在(l,+∞)上的最大值为8,
∴函数≤8,在(l,+∞)上恒成立.
化为:a≤(2x3﹣7x2+8x)min,x∈(l,+∞).
令f(x)=2x3﹣7x2+8x,x∈(l,+∞).
则f′(x)=6x2﹣14x+8=2(3x﹣4)(x﹣1),
可得x=时,函数f(x)取得极小值即最小值,=.
∴实数a的值为.
故答案为:.
二、解答题(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤)
15.【解答】解:z==.
(1)若z是纯虚数,则,即m=2;
(2),
由在复平面上对应的点在第四象限,得,即﹣2<m<2.
16.【解答】解:(1)当p为真时,即函数f(x)=x2﹣2mx+1在(﹣∞,1)上单调递减,则m≥1,
当q为真时,即:?x∈R,x2+2x+m≥0,则△=(2)2﹣4m≤0,即m≥3,
“p且q”为真,则p为真且q为真,
即,即m≥3;
(2)由“p或q”为真,“p且q”为假,则p、q一真一假,
由(1)得:
即,解得:1≤m<3.
17.【解答】解:(1)分析法:要证明[f(x1)+f(x2)]<f();
即证明+<2,
即证明(+)2<(2)2,
即x1+x2+2<4×=2(x1+x2)
即证明2<x1+x2,
∵x1,x2∈[0,+∞),且x1≠x2,
∴2<x1+x2,成立,即[f(x1)+f(x2)]<f();
(2)反证法:
假设结论不成立,即a>b,
∵若f(x)为R上的增函数,
∴g(x)=x+f(x)在R上为增函数,
则g(a)>g(b),即a+f(a)>b+f(b),与已知a+f(a)≤b+f(b)矛盾,
即假设不成立,则原命题成立.
18.【解答】解:(1)由已知可知P(t,),故直线MN的斜率为﹣,
∴直线MN的方程为y=﹣(x﹣t)+,
令y=0可得x=2t,∴M(2t,0).
又E(1,0),∠OEF=45°,
∴直线EF的方程为y=﹣x+1,
联立方程组,解得x=,y=,
∴yN=,
∴S(t)==(2t﹣1)?=(≤t≤5).
(2)S′(t)=.
∴当≤t<2时,S′(t)<0,当2<t≤时,S′(t)>0,
∴当t=2时,S(t)取得最小值S(2)=.
∴当t=2时,△EMN面积最小,最小面积为.
19.【解答】解:(1)∵椭圆C:的右准线方程为x=4,右顶点为A(2,0).
∴,a=2,∴c=1,b2=a2﹣c2=3,
∴椭圆C的方程为.
(2)①∵△OPA为等腰直角三角形且直角顶点P在x轴上方.
∴OP的方程为:y=x,AP的方程为:y=x﹣2.
由可得P(1,1).
设M(x1,y1),N(x2,y2).则x1+x2=2,y1+y2=2
∴,,
两式相减可得=0.∴kMN
∵kOP=1,∴=﹣,即k.
∴直线MN的方程为y﹣1=﹣(x﹣1),即3x+4y﹣7=0.
②设AM的斜率为k,∵点P是线段MN的中点,点Q是线段NA的中点,∴kPQ=k.
∵∠OPQ的角平分线与x轴垂直,∴kOP+kPQ=0,∴kOP=﹣k.
由①可得kMN,∴.
设AM的方程为y=k(x﹣2).
由可得(3+4k2)x2﹣16k2x+16k2﹣12=0.
∴2,
∴x,,
以﹣换k,可得,y,
∴=,
整理可得:10k4+7k2﹣3=0,解得,k=±.
∴直线AM的斜率为.
20.【解答】解:(1)函数f(x)=xlnx的导数为f′(x)=1+lnx,
由f′(x)>0,可得x>;由f′(x)<0,可得0<x<;
即f(x)的增区间为(,+∞),减区间为(0,);
(2)证明:设F(x)=﹣lnx﹣(x>0),
可得F′(x)=﹣+=,
当x>1时,ex>1,F′(x)>0,F(x)递增;
当0<x<1时,ex>1,F′(x)<0,F(x)递减;
可得F(x)的最小值为F(1)=e﹣1>0,
即有﹣lnx﹣>0,即为xlnx+1<ex,可得g(x)>f(x)+1;
(3)f(x)+g(x)≥h(x)恒成立?k≤恒成立,
令m(x)=,m′(x)==,
令r(x)=ex﹣﹣lnx+e+1﹣,r′(x)==,
设G(x)=ex﹣x+1,可得G′(x)=ex﹣1,当x>0时,G(x)递增,可得G(x)>G(0)=0,
即有ex>x+1,即有r′(x)>0,r(x)在x>0递增,r(1)=0,
而在(0,1)上,r(x)<0;m(x)在(0,1)递减;
在[1,+∞)上r(x)>0,m(x)在[1,+∞)递增,可得m(x)的最小值为m(1)=,即k≤,
综上可得k的取值范围是(﹣∞,].
一、填空题(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上)
1.(5分)命题:“若a=0,则ab=0”的逆否命题是 .
2.(5分)已知复数z=2﹣i(i是虚数单位),则|z|= .
3.(5分)已知椭圆,则椭圆的焦点坐标是 .
4.(5分)“(x+2)(x﹣1)<0”是“﹣3<x<1”成立的 条件(在“充分不必要”,“必要不充分”,“充要”,“既不充分又不必要”中选一个填写).
5.(5分)函数f(x)=sinx﹣x,x∈(0,)的单调递增区间是 .
6.(5分)若双曲线C:(a>0,b>0)的离心率为,则的值为 .
7.(5分)直线l过点(0,1),且与曲线y=f(x)相切于点(a,3),若f'(a)=1,则实数a的值是 .
8.(5分)古埃及发现如下有趣等式:,,,,…,按此规律,= (n∈N*).
9.(5分)函数f(x)的定义域为R,若对任意的x∈R,f(x)+xf'(x)>0,且,则不等式(x2+1)f(x2+1)>1的解集为 .
10.(5分)在实数中:要证明实数a,b相等,可以利用a≤b且a≥b来证明:类比到集合中:要证明集合A,B相等,可以利用 来证明.
11.(5分)已知椭圆C:,过点P(0,6)的直线l与椭圆C交于A,B两点,若A是线段PB的中点,则点A的坐标为 .
12.(5分)若定义在R上的函数f(x)=|x3﹣3x2+m|有三个不同的单调递增区间,则实数m的取值范围是 .
13.(5分)已知椭圆C:的右焦点为F(2,0),F关于直线的对称点Q在椭圆C上,则b= .
14.(5分)若函数在(l,+∞)上的最大值为8,则实数a的值为 .
二、解答题(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤)
15.(14分)已知复数z=,(m∈R,i是虚数单位)
(1)若z是纯虚数,求m的值;
(2)设是z的共轭复数,在复平面上对应的点在第四象限,求m的取值范围.
16.(14分)已知p:函数f(x)=x2﹣2mx+1在(﹣∞,1)上单调递减(其中m∈R),q:?x∈R,x2+2x+m≥0(其中m∈R).
(1)如果“p且q”为真,求实数m的取值范围.
(2)如果“p或q”为真,“p且q”为假,求实数m的取值范围.
17.(14分)(1)已知f(x)=,x∈[0,+∞),若x1,x2∈[0,+∞),且x1≠x2,求证:[f(x1)+f(x2)]<f();
(2)用反证法证明:若f(x)为R上的增函数,且a+f(a)≤b+f(b),求证:a≤b.
18.(16分)如图,以两条互相垂直的公路所在直线分别为x轴,y轴建立平面直角坐标系,公路附近有一居民区EFG和一风景区,其中OE=1(单位:百米),∠OEF=45°,风景区的部分边界为曲线C,曲线C的方程为y=(≤x≤5),拟在居民和风景区间辟出一个三角形区域EMN用于工作人员办公,点M,N分别在x轴和EF上,且MN与曲线C相切于P点.
(1)设P点的横坐标为t,写出△EMN面积的函数表达式S(t);
(2)当t为何值时,△EMN面积最小?并求出最小面积.
19.(16分)在平面直角坐标系xOy中,已知椭圆C:的右准线方程为x=4,右顶点为A(2,0).
(1)求椭圆C的方程;
(2)若M,N是椭圆C上不同于A的两点,点P是线段MN的中点.
①如图1,若△OPA为等腰直角三角形且直角顶点P在x轴上方,求直线MN的方程;
②如图2所示,点Q是线段NA的中点,若AM⊥AN且∠OPQ的角平分线与x轴垂直,求直线AM的斜率.
20.(16分)已知函数f(x)=xlnx,g(x)=ex,h(x)=kx2+ex﹣(k∈R),其中e为自然对数的底数.
(1)求函数y=f(x)的单调区间;
(2)求证:g(x)>f(x)+1;
(3)若f(x)+g(x)≥h(x)恒成立,求实数k的取值范围.
2018-2019学年江苏省泰州市高二(上)期末数学试卷(文科)
参考答案与试题解析
一、填空题(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上)
1.【解答】解:∵:“若a=0,则ab=0”
∴逆否命题:若ab≠0,则a≠0
故答案为:若ab≠0,则a≠0
2.【解答】解:∵复数z=2﹣i,
∴|z|===.
故答案为:.
3.【解答】解:∵椭圆,∴a2=25,b2=16
∴c2=a2﹣b2=9
∴c=3
∴椭圆的焦点坐标是(﹣3,0),(3,0)
故答案为:(﹣3,0),(3,0)
4.【解答】解:(x+2)(x﹣1)<0,解得﹣2<x<1.
∴“(x+2)(x﹣1)<0”是“﹣3<x<1”成立的充分不必要条件.
故答案为:充分不必要.
5.【解答】解:由f(x)=sinx﹣x,x∈(0,),得f′(x)=cosx﹣,
由f′(x)=cosx﹣>0,得cosx>,
∵x∈(0,),∴x∈(0,),
则f(x)的单调递增区间为(0,).
故答案为:(0,).
6.【解答】解:双曲线C:(a>0,b>0)的离心率为,
可得e==,可得a2+b2=10a2,可得=3.
故答案为:3.
7.【解答】解:直线l经过点(0,1),且与曲线y=f(x)相切于点(a,3).若f′(a)=1,
切线的斜率为1,切线方程为:y﹣1=x,
所以3﹣1=a,解得a=2.
故答案为:2.
8.【解答】解:由,,,,…,可归纳出:=+,
故答案为:+,
9.【解答】解:令g(x)=xf(x),则g′(x)=f(x)+xf'(x)>0,
可得g(x)在(﹣∞,+∞)上为增函数,
由,得g(2)=2f(2)=1,
∴不等式(x2+1)f(x2+1)>1化为g(x2+1)>g(2),
又g(x)在(﹣∞,+∞)上为增函数,
∴x2+1>2,得x<﹣1或x>1.
∴不等式(x2+1)f(x2+1)>1的解集为(﹣∞,﹣1)∪(1,+∞).
故答案为:(﹣∞,﹣1)∪(1,+∞).
10.【解答】解:在实数中:要证明实数a,b相等,可以利用a≤b且a≥b来证明:类比到集合中:要证明集合A,B相等,可以利用 A?B且B?A来证明.
故答案为:A?B且B?A.
11.【解答】解:易知直线的斜率存在,设直线AB的方程y=kx+6,设A(x1,y1),B(x2,y2),
∵A是线段PB的中点,
∴2x1=x2,①
由,消y整理可得(3+4k2)x2+48kx+96=0,
∴x1+x2=﹣,②,x1x2=,③,
由①②③可得=,
整理解得4k2=9,
∴x12==4,
∴x1=±2,
∴y1=±3,
∴A(2,3)或(﹣2,3)
故答案为:(2,3)或(﹣2,3)
12.【解答】解:令g(x)=x3﹣3x2+m,由g′(x)=3x2﹣6x=0可得,x=0或x=2.
g(x)在(﹣∞,0),(2,+∞)递增,在(0,2)递减.
要使函数f(x)=|x3﹣3x2+m|有三个不同的单调递增区间,则g(x)的图象只能如下图所示,
∴∴0<m<4.
故答案为:(0,4).
13.【解答】解:设Q(m,n),
由F关于直线的对称点Q在椭圆C上,
∴?=﹣1,=?(),
解得m=,n=,
∵点Q在椭圆上,且a2=4+b2,
∴+=1,
整理可得b2(b2+4)2=256,
∴b(b2+4)=16,
解得b=2,
故答案为:2
14.【解答】解:函数在(l,+∞)上的最大值为8,
∴函数≤8,在(l,+∞)上恒成立.
化为:a≤(2x3﹣7x2+8x)min,x∈(l,+∞).
令f(x)=2x3﹣7x2+8x,x∈(l,+∞).
则f′(x)=6x2﹣14x+8=2(3x﹣4)(x﹣1),
可得x=时,函数f(x)取得极小值即最小值,=.
∴实数a的值为.
故答案为:.
二、解答题(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤)
15.【解答】解:z==.
(1)若z是纯虚数,则,即m=2;
(2),
由在复平面上对应的点在第四象限,得,即﹣2<m<2.
16.【解答】解:(1)当p为真时,即函数f(x)=x2﹣2mx+1在(﹣∞,1)上单调递减,则m≥1,
当q为真时,即:?x∈R,x2+2x+m≥0,则△=(2)2﹣4m≤0,即m≥3,
“p且q”为真,则p为真且q为真,
即,即m≥3;
(2)由“p或q”为真,“p且q”为假,则p、q一真一假,
由(1)得:
即,解得:1≤m<3.
17.【解答】解:(1)分析法:要证明[f(x1)+f(x2)]<f();
即证明+<2,
即证明(+)2<(2)2,
即x1+x2+2<4×=2(x1+x2)
即证明2<x1+x2,
∵x1,x2∈[0,+∞),且x1≠x2,
∴2<x1+x2,成立,即[f(x1)+f(x2)]<f();
(2)反证法:
假设结论不成立,即a>b,
∵若f(x)为R上的增函数,
∴g(x)=x+f(x)在R上为增函数,
则g(a)>g(b),即a+f(a)>b+f(b),与已知a+f(a)≤b+f(b)矛盾,
即假设不成立,则原命题成立.
18.【解答】解:(1)由已知可知P(t,),故直线MN的斜率为﹣,
∴直线MN的方程为y=﹣(x﹣t)+,
令y=0可得x=2t,∴M(2t,0).
又E(1,0),∠OEF=45°,
∴直线EF的方程为y=﹣x+1,
联立方程组,解得x=,y=,
∴yN=,
∴S(t)==(2t﹣1)?=(≤t≤5).
(2)S′(t)=.
∴当≤t<2时,S′(t)<0,当2<t≤时,S′(t)>0,
∴当t=2时,S(t)取得最小值S(2)=.
∴当t=2时,△EMN面积最小,最小面积为.
19.【解答】解:(1)∵椭圆C:的右准线方程为x=4,右顶点为A(2,0).
∴,a=2,∴c=1,b2=a2﹣c2=3,
∴椭圆C的方程为.
(2)①∵△OPA为等腰直角三角形且直角顶点P在x轴上方.
∴OP的方程为:y=x,AP的方程为:y=x﹣2.
由可得P(1,1).
设M(x1,y1),N(x2,y2).则x1+x2=2,y1+y2=2
∴,,
两式相减可得=0.∴kMN
∵kOP=1,∴=﹣,即k.
∴直线MN的方程为y﹣1=﹣(x﹣1),即3x+4y﹣7=0.
②设AM的斜率为k,∵点P是线段MN的中点,点Q是线段NA的中点,∴kPQ=k.
∵∠OPQ的角平分线与x轴垂直,∴kOP+kPQ=0,∴kOP=﹣k.
由①可得kMN,∴.
设AM的方程为y=k(x﹣2).
由可得(3+4k2)x2﹣16k2x+16k2﹣12=0.
∴2,
∴x,,
以﹣换k,可得,y,
∴=,
整理可得:10k4+7k2﹣3=0,解得,k=±.
∴直线AM的斜率为.
20.【解答】解:(1)函数f(x)=xlnx的导数为f′(x)=1+lnx,
由f′(x)>0,可得x>;由f′(x)<0,可得0<x<;
即f(x)的增区间为(,+∞),减区间为(0,);
(2)证明:设F(x)=﹣lnx﹣(x>0),
可得F′(x)=﹣+=,
当x>1时,ex>1,F′(x)>0,F(x)递增;
当0<x<1时,ex>1,F′(x)<0,F(x)递减;
可得F(x)的最小值为F(1)=e﹣1>0,
即有﹣lnx﹣>0,即为xlnx+1<ex,可得g(x)>f(x)+1;
(3)f(x)+g(x)≥h(x)恒成立?k≤恒成立,
令m(x)=,m′(x)==,
令r(x)=ex﹣﹣lnx+e+1﹣,r′(x)==,
设G(x)=ex﹣x+1,可得G′(x)=ex﹣1,当x>0时,G(x)递增,可得G(x)>G(0)=0,
即有ex>x+1,即有r′(x)>0,r(x)在x>0递增,r(1)=0,
而在(0,1)上,r(x)<0;m(x)在(0,1)递减;
在[1,+∞)上r(x)>0,m(x)在[1,+∞)递增,可得m(x)的最小值为m(1)=,即k≤,
综上可得k的取值范围是(﹣∞,].
同课章节目录
