勾股定理应用——蚂蚁爬行问题中的最短路程问题课件(共16张PPT)
文档属性
| 名称 | 勾股定理应用——蚂蚁爬行问题中的最短路程问题课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 365.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 14:44:45 | ||
图片预览


文档简介
课件16张PPT。蚂蚁爬行问题中的最短
路程问题
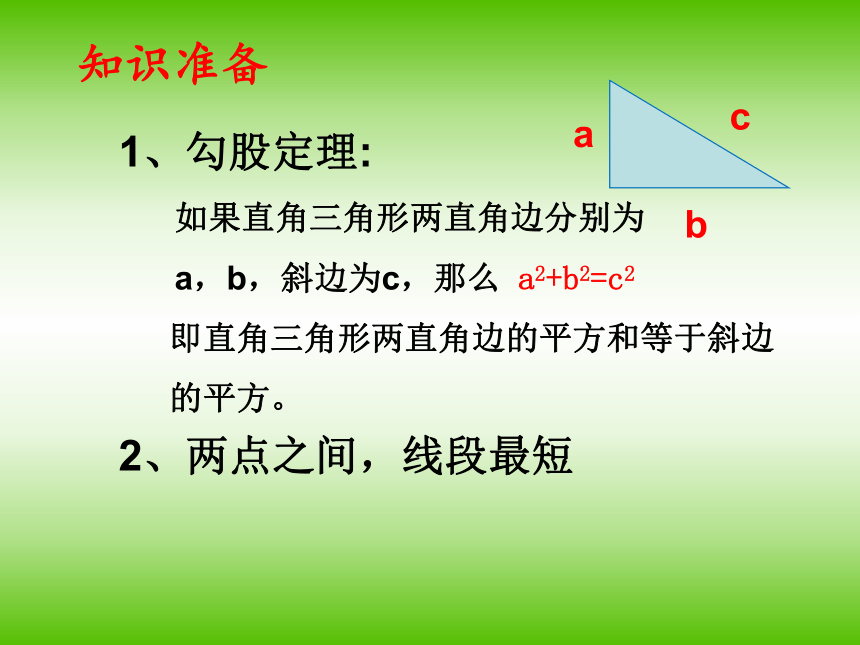
知识准备2、两点之间,线段最短1、勾股定理:
如果直角三角形两直角边分别为
a,b,斜边为c,那么 a2+b2=c2
即直角三角形两直角边的平方和等于斜边
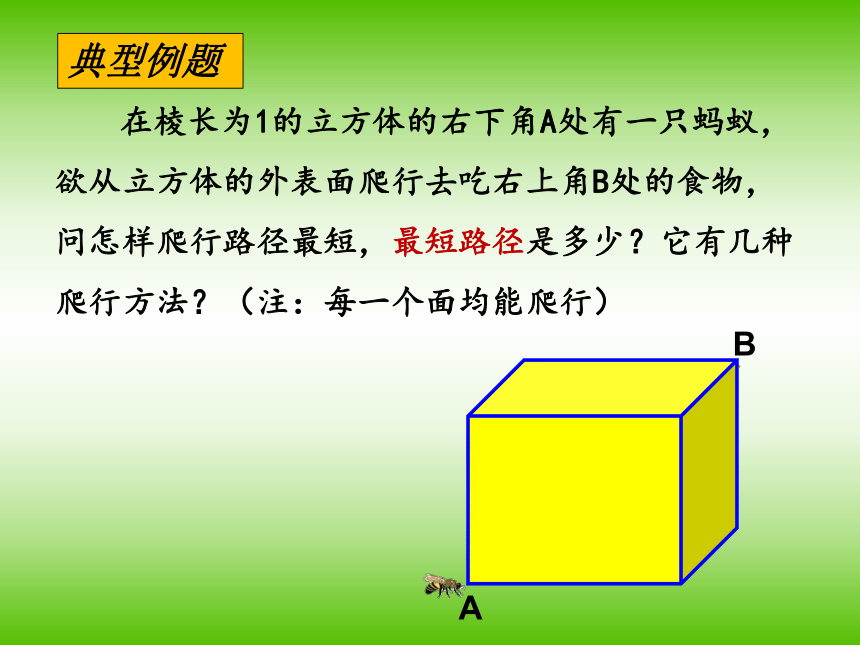
的平方。abc 在棱长为1的立方体的右下角A处有一只蚂蚁,
欲从立方体的外表面爬行去吃右上角B处的食物,
问怎样爬行路径最短,最短路径是多少?它有几种
爬行方法?(注:每一个面均能爬行)典型例题思路点拨1、在立体图形中,怎样利用线段公理解决路径
最短问题?
2、怎样展开立方体的表面?展开哪几个面呢?
3、和A相连的面有哪几个?和B相连的面有哪几个?
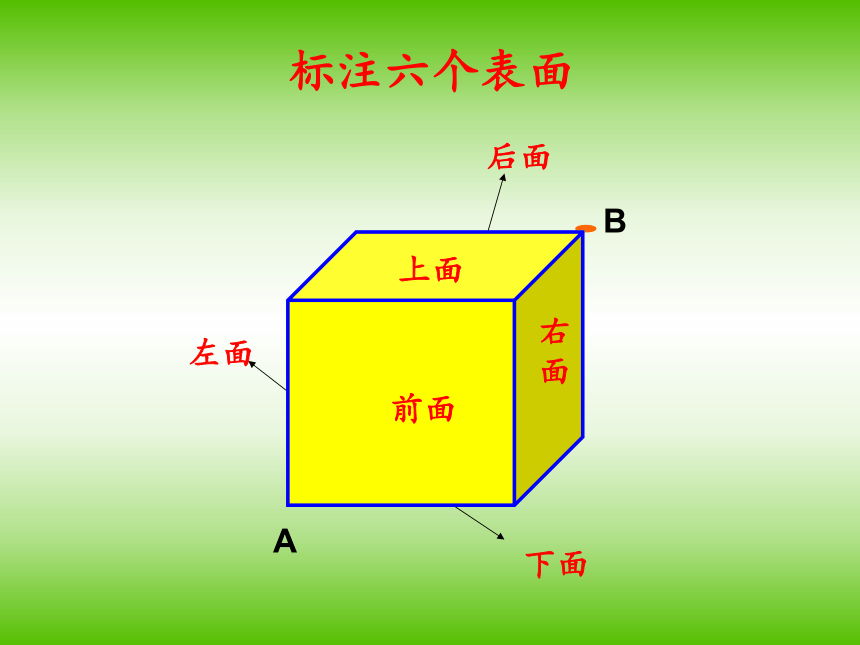
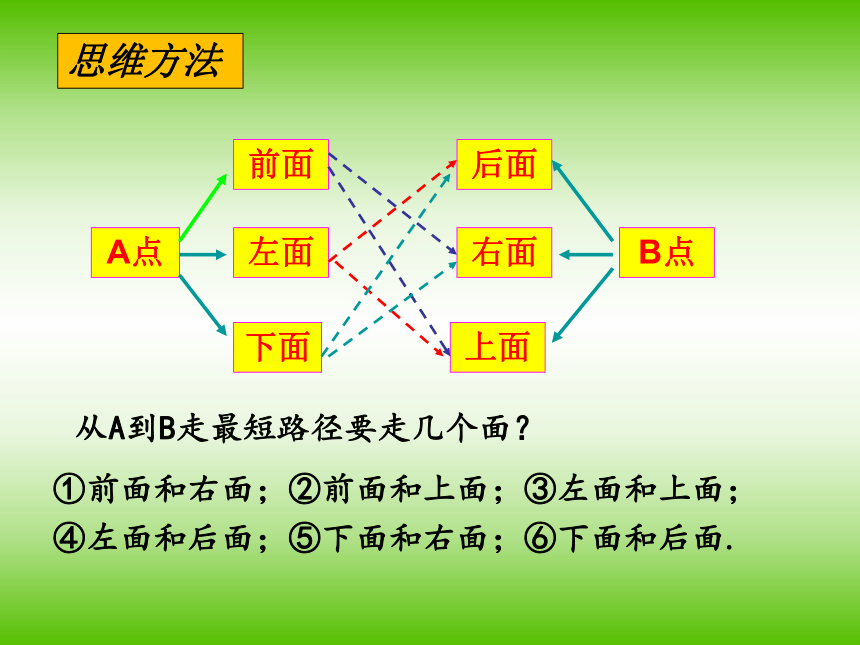
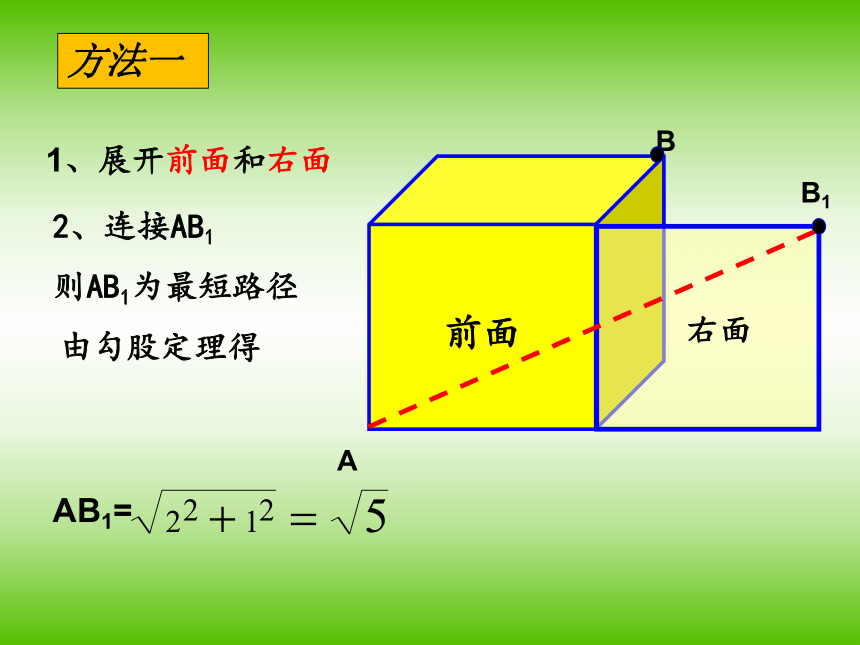
4、最短路径要走几个面?怎么走?后面左面下面标注六个表面上面前面右面A点前面左面下面上面右面后面B点从A到B走最短路径要走几个面?①前面和右面;②前面和上面;③左面和上面;④左面和后面;⑤下面和右面;⑥下面和后面.思维方法AB1B1、展开前面和右面2、连接AB1则AB1为最短路径由勾股定理得方法一前面右面1、展开前面和上面2、连接AB2则AB2为最短路径由勾股定理得AB2B方法二前面上面2、连接A1B3则A1B3为最短路径1、展开左面和上面由勾股定理得方法三上面左面2、连接AB4则AB4为最短路径,1、展开左面和后面由勾股定理得B4方法四左面后面2、连接AB5则AB5为最短路径1、展开下面和右面由勾股定理得AB5B方法五右面下面2、连接AB6则AB6为最短路径1、展开下面和后面由勾股定理得B6方法六后面下面从A到B共有六种最短路径总结立体图形表面两点间“最短路程”的一般策略:方法提炼异面两点求最短;
立体化归成平面;
展开分类罗列全;
比较长短答案现;立体图形中的“最短路程”谢谢聆听!
知识准备2、两点之间,线段最短1、勾股定理:
如果直角三角形两直角边分别为
a,b,斜边为c,那么 a2+b2=c2
即直角三角形两直角边的平方和等于斜边
的平方。abc 在棱长为1的立方体的右下角A处有一只蚂蚁,
欲从立方体的外表面爬行去吃右上角B处的食物,
问怎样爬行路径最短,最短路径是多少?它有几种
爬行方法?(注:每一个面均能爬行)典型例题思路点拨1、在立体图形中,怎样利用线段公理解决路径
最短问题?
2、怎样展开立方体的表面?展开哪几个面呢?
3、和A相连的面有哪几个?和B相连的面有哪几个?
4、最短路径要走几个面?怎么走?后面左面下面标注六个表面上面前面右面A点前面左面下面上面右面后面B点从A到B走最短路径要走几个面?①前面和右面;②前面和上面;③左面和上面;④左面和后面;⑤下面和右面;⑥下面和后面.思维方法AB1B1、展开前面和右面2、连接AB1则AB1为最短路径由勾股定理得方法一前面右面1、展开前面和上面2、连接AB2则AB2为最短路径由勾股定理得AB2B方法二前面上面2、连接A1B3则A1B3为最短路径1、展开左面和上面由勾股定理得方法三上面左面2、连接AB4则AB4为最短路径,1、展开左面和后面由勾股定理得B4方法四左面后面2、连接AB5则AB5为最短路径1、展开下面和右面由勾股定理得AB5B方法五右面下面2、连接AB6则AB6为最短路径1、展开下面和后面由勾股定理得B6方法六后面下面从A到B共有六种最短路径总结立体图形表面两点间“最短路程”的一般策略:方法提炼异面两点求最短;
立体化归成平面;
展开分类罗列全;
比较长短答案现;立体图形中的“最短路程”谢谢聆听!
