【鲁教版七下精美学案】8.4 平行线的判定定理(知识梳理+考点突破+巩固提高+真题训练)
文档属性
| 名称 | 【鲁教版七下精美学案】8.4 平行线的判定定理(知识梳理+考点突破+巩固提高+真题训练) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 09:47:55 | ||
图片预览


文档简介
8.4 平行线的判定定理
知 识 梳 理
知识点1 平行线的判定公理
同位角相等,两直线平行。
符号语言:∵_______________,
∴________________.
知识点2 平行线的判定定理
(1)同旁内角互补,两直线平行.
符号语言:∵_______________,
∴________________.
(2)内错角相等,两直线平行
符号语言:∵_______________,
∴________________.
注意 平行线的判定方法有三个.因此证两直线平行有三种思路,在具体证题时,根据条件选取最合适的证法.
考 点 突 破
考点: 平行线的判定
【典例】如图所示,∠ABC=∠BCD=120°,BE⊥AB,CF⊥CD.求证:BE∥CF。
思路导析:注意运用逆向思维的方法,从要证明的结论出发,得出需要的条件,本题中∠EBC和∠BCF是被截线BE,CF与截线BC所形成的内错角,只要证明∠EBC=∠BCF就能证出结论BE∥CF.
证明:∵BE⊥AB,CF⊥CD(已知),∴∠ABE=∠FCD=90°(垂直的定义)
∵∠ABC=∠BCD=120°(已知),∴∠ABC-∠ABE=∠BCD-∠FCD(等式的性质),
即∠EBC=∠BCF(等量代换)∴BE∥CF(内错角相等,两直线平行)
友情提示 平行线的判定公理和判定定理是根据两角的关系判定两条直线的位置关系的.在做题时,分清截线和被截线、分清“三线八角”的位置关系是应用公理、定理的前提。
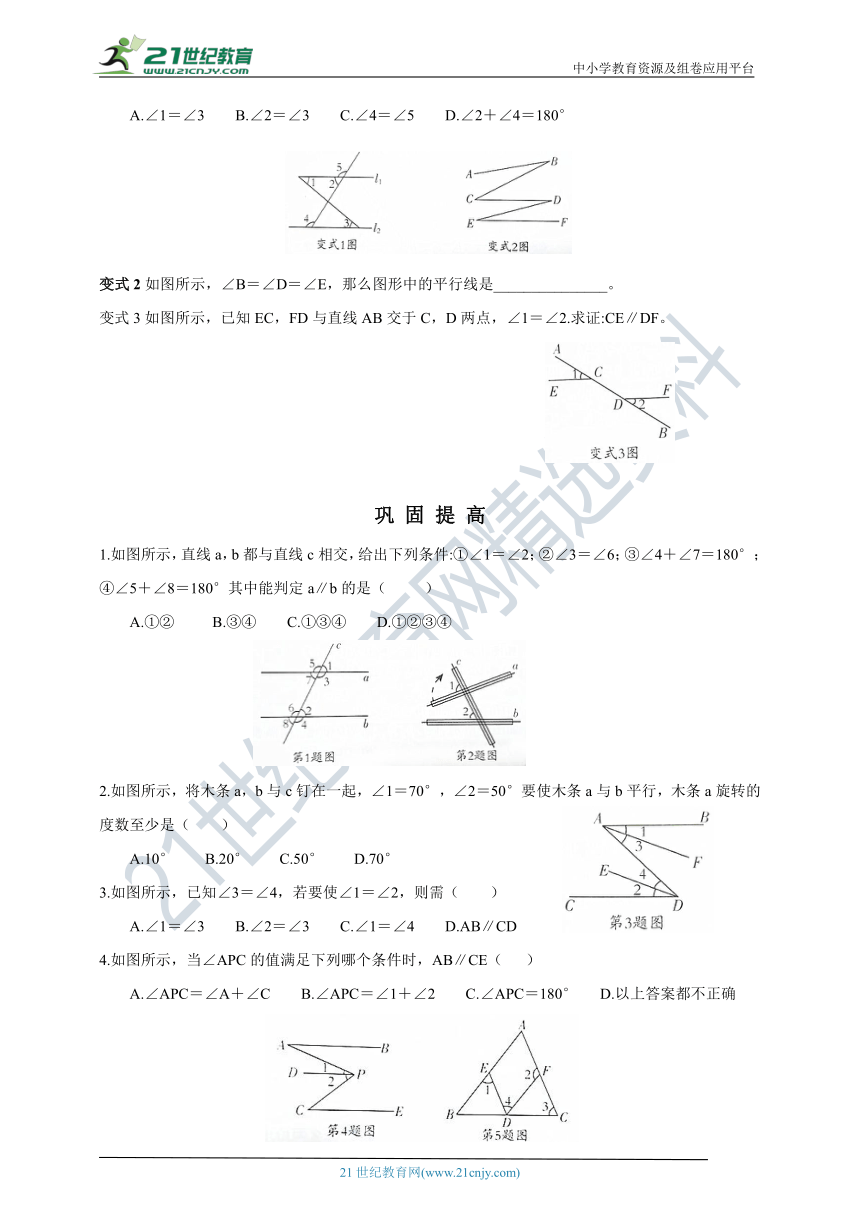
变式1 如图所示,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
变式2如图所示,∠B=∠D=∠E,那么图形中的平行线是_______________。
变式3如图所示,已知EC,FD与直线AB交于C,D两点,∠1=∠2.求证:CE∥DF。
巩 固 提 高
1.如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°其中能判定a∥b的是( )
A.①② B.③④ C.①③④ D.①②③④
2.如图所示,将木条a,b与c钉在一起,∠1=70°,∠2=50°要使木条a与b平行,木条a旋转的度数至少是( )
A.10° B.20° C.50° D.70°
3.如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.AB∥CD
4.如图所示,当∠APC的值满足下列哪个条件时,AB∥CE( )
A.∠APC=∠A+∠C B.∠APC=∠1+∠2 C.∠APC=180° D.以上答案都不正确
5.如图所示,在下列结论给出的条件中,不能判定AB∥DF的是( )
A.∠2+∠A=180° B.∠3=∠A C.∠1=∠4 D.∠B=∠FDC
6.如图所示是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
7.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图①所示,展开后,测得∠1=∠2
B.如图②所示,展开后,测得∠1=∠2,且∠3=∠4
C.如图③所示,测得∠1=∠2
D.如图④所示,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
8.如图所示,推理填空:
(1)∵∠A=∠___________(已知),∴AC∥ED( )
(2)∵∠2=∠___________(已知),∴AC∥ED( )
(3)∵∠A+∠AFD=180°(已知),∴AB∥FD( )
(4)∵∠2+∠____=180°(已知),∴AC∥ED( )
9.如图所示,可以得到DE∥BC的条件是___________________。
10.如图所示,如果∠1=∠2,那么下面结论正确的是______________。
①AD∥BC ②AB∥CD ③∠3=∠4 ④∠A=∠C
11.如图所示,已知∠A=∠F,∠C=∠D,试说明BD∥CE。
真 题 训 练
1.(2018·郴州)如图所示,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠2=∠4
B.∠1+∠4=180°
C.∠5=∠4
D.∠1=∠3
2.(2018·湘潭)如图所示,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为_______________。(任意添加一个符合题意的条件即可)
3.(淄博中考)如图所示,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,
∠3=130°,找出图中的平行线,并说明理由。
参考答案及解析
知识梳理
知识点1: ∠1=∠2 a∥b
知识点2:(1)∠1+∠2=180° a∥b (2)∠1=∠2 a∥b
考点突破
1.B 2.CD∥EF
3.证明:∵∠1+∠ECD=180°,∠2+∠FDC=180°(平角定义),
∴∠ECD=180°- ∠1,∠FDC=180 - ∠2(等式性质)
又∵∠1=∠2(已知),∴∠ECD=∠FDC(等量代换)
∴CE∥DF(内错角相等,两直线平行)
巩固提高
1.D 2.B 3.D 4.A 5.B 6.A 7.C
8.(1)BED 同位角相等,两直线平行
(2)DFC 内错角相等,两直线平行
(3)同旁内角互补,两直线平行
(4)AFD 同旁内角互补,两直线平行
9.答案不唯一,比如∠DAB=∠B,∠EAC=∠C,∠EAB+∠B=180°,∠DAC+∠C=180°
10.②
11.证明:∵∠A=∠F(已知),
∴AC∥DF(内错角相等,两直线平行)
∴∠C=∠CEF(两直线平行,内错角相等)
∵∠C=∠D(已知),
∴∠D=∠CEF(等量代换)
∴BD∥CE(同位角相等,两直线平行)
真题训练
1.D
2.∠CBD=∠BDA(或者∠C=∠CDE,或者∠C+∠CDA=180°,以及∠CBA+∠A=180°中的一个即可)
3.解:OA∥BC,OB∥AC
理由:∵∠1=50°,∠2=50°,∴∠1=∠2。 ∴OB∥AC.
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°
∴OA∥BC.
知 识 梳 理
知识点1 平行线的判定公理
同位角相等,两直线平行。
符号语言:∵_______________,
∴________________.
知识点2 平行线的判定定理
(1)同旁内角互补,两直线平行.
符号语言:∵_______________,
∴________________.
(2)内错角相等,两直线平行
符号语言:∵_______________,
∴________________.
注意 平行线的判定方法有三个.因此证两直线平行有三种思路,在具体证题时,根据条件选取最合适的证法.
考 点 突 破
考点: 平行线的判定
【典例】如图所示,∠ABC=∠BCD=120°,BE⊥AB,CF⊥CD.求证:BE∥CF。
思路导析:注意运用逆向思维的方法,从要证明的结论出发,得出需要的条件,本题中∠EBC和∠BCF是被截线BE,CF与截线BC所形成的内错角,只要证明∠EBC=∠BCF就能证出结论BE∥CF.
证明:∵BE⊥AB,CF⊥CD(已知),∴∠ABE=∠FCD=90°(垂直的定义)
∵∠ABC=∠BCD=120°(已知),∴∠ABC-∠ABE=∠BCD-∠FCD(等式的性质),
即∠EBC=∠BCF(等量代换)∴BE∥CF(内错角相等,两直线平行)
友情提示 平行线的判定公理和判定定理是根据两角的关系判定两条直线的位置关系的.在做题时,分清截线和被截线、分清“三线八角”的位置关系是应用公理、定理的前提。
变式1 如图所示,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
变式2如图所示,∠B=∠D=∠E,那么图形中的平行线是_______________。
变式3如图所示,已知EC,FD与直线AB交于C,D两点,∠1=∠2.求证:CE∥DF。
巩 固 提 高
1.如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°其中能判定a∥b的是( )
A.①② B.③④ C.①③④ D.①②③④
2.如图所示,将木条a,b与c钉在一起,∠1=70°,∠2=50°要使木条a与b平行,木条a旋转的度数至少是( )
A.10° B.20° C.50° D.70°
3.如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.AB∥CD
4.如图所示,当∠APC的值满足下列哪个条件时,AB∥CE( )
A.∠APC=∠A+∠C B.∠APC=∠1+∠2 C.∠APC=180° D.以上答案都不正确
5.如图所示,在下列结论给出的条件中,不能判定AB∥DF的是( )
A.∠2+∠A=180° B.∠3=∠A C.∠1=∠4 D.∠B=∠FDC
6.如图所示是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
7.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图①所示,展开后,测得∠1=∠2
B.如图②所示,展开后,测得∠1=∠2,且∠3=∠4
C.如图③所示,测得∠1=∠2
D.如图④所示,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
8.如图所示,推理填空:
(1)∵∠A=∠___________(已知),∴AC∥ED( )
(2)∵∠2=∠___________(已知),∴AC∥ED( )
(3)∵∠A+∠AFD=180°(已知),∴AB∥FD( )
(4)∵∠2+∠____=180°(已知),∴AC∥ED( )
9.如图所示,可以得到DE∥BC的条件是___________________。
10.如图所示,如果∠1=∠2,那么下面结论正确的是______________。
①AD∥BC ②AB∥CD ③∠3=∠4 ④∠A=∠C
11.如图所示,已知∠A=∠F,∠C=∠D,试说明BD∥CE。
真 题 训 练
1.(2018·郴州)如图所示,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠2=∠4
B.∠1+∠4=180°
C.∠5=∠4
D.∠1=∠3
2.(2018·湘潭)如图所示,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为_______________。(任意添加一个符合题意的条件即可)
3.(淄博中考)如图所示,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,
∠3=130°,找出图中的平行线,并说明理由。
参考答案及解析
知识梳理
知识点1: ∠1=∠2 a∥b
知识点2:(1)∠1+∠2=180° a∥b (2)∠1=∠2 a∥b
考点突破
1.B 2.CD∥EF
3.证明:∵∠1+∠ECD=180°,∠2+∠FDC=180°(平角定义),
∴∠ECD=180°- ∠1,∠FDC=180 - ∠2(等式性质)
又∵∠1=∠2(已知),∴∠ECD=∠FDC(等量代换)
∴CE∥DF(内错角相等,两直线平行)
巩固提高
1.D 2.B 3.D 4.A 5.B 6.A 7.C
8.(1)BED 同位角相等,两直线平行
(2)DFC 内错角相等,两直线平行
(3)同旁内角互补,两直线平行
(4)AFD 同旁内角互补,两直线平行
9.答案不唯一,比如∠DAB=∠B,∠EAC=∠C,∠EAB+∠B=180°,∠DAC+∠C=180°
10.②
11.证明:∵∠A=∠F(已知),
∴AC∥DF(内错角相等,两直线平行)
∴∠C=∠CEF(两直线平行,内错角相等)
∵∠C=∠D(已知),
∴∠D=∠CEF(等量代换)
∴BD∥CE(同位角相等,两直线平行)
真题训练
1.D
2.∠CBD=∠BDA(或者∠C=∠CDE,或者∠C+∠CDA=180°,以及∠CBA+∠A=180°中的一个即可)
3.解:OA∥BC,OB∥AC
理由:∵∠1=50°,∠2=50°,∴∠1=∠2。 ∴OB∥AC.
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°
∴OA∥BC.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
