北师大版数学八年级下册 1.4《角平分线(二)》 课件 共25张PPT
文档属性
| 名称 | 北师大版数学八年级下册 1.4《角平分线(二)》 课件 共25张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 242.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 18:17:59 | ||
图片预览





文档简介
课件25张PPT。1.4 角平分线 (2)
一 回顾与思考
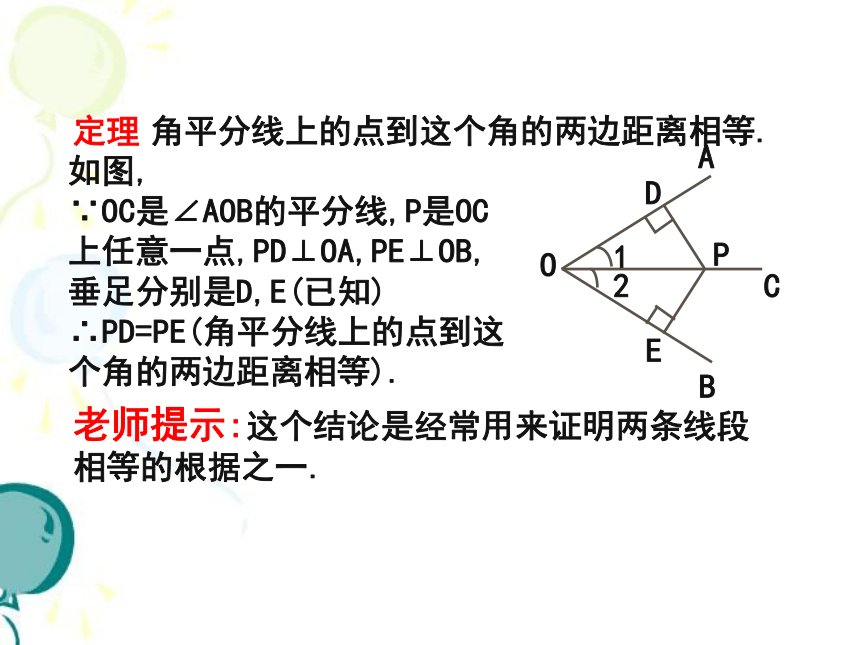
定理 角平分线上的点到这个角的两边距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.如图,
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
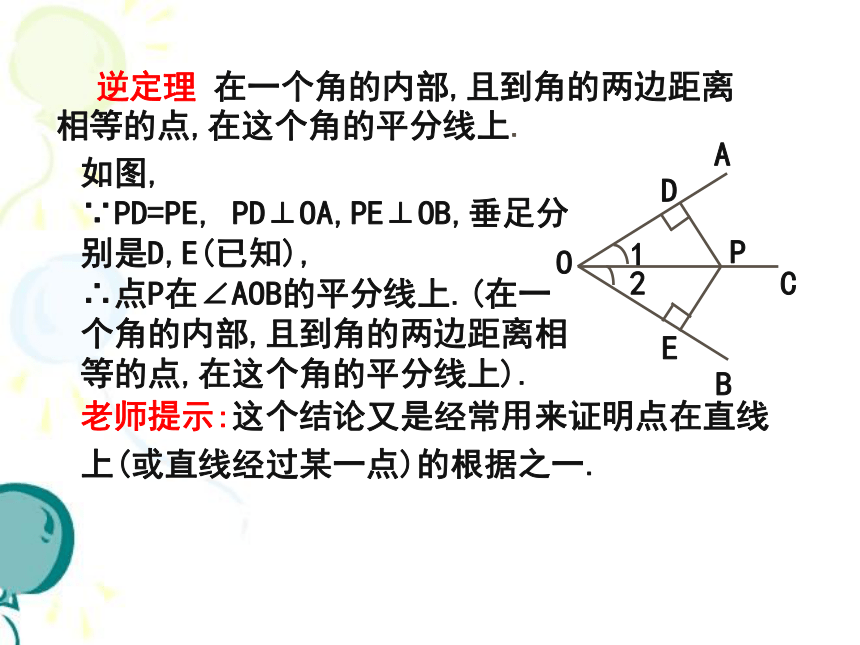
∴PD=PE(角平分线上的点到这个角的两边距离相等). 逆定理 在一个角的内部,且到角的两边距离 相等的点,在这个角的平分线上.如图,
∵PD=PE, PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).老师提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
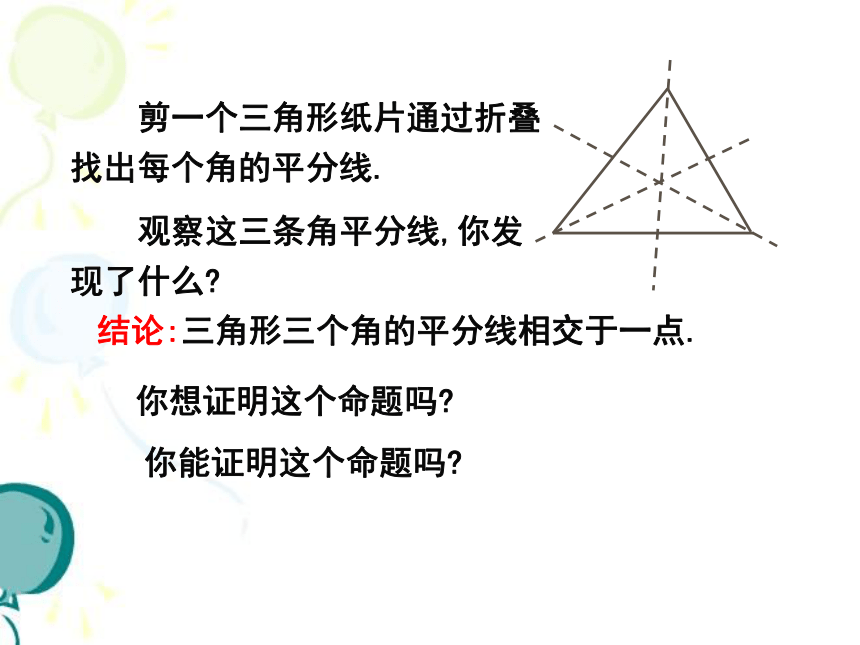
二 探究新知 剪一个三角形纸片通过折叠找出每个角的平分线. 结论:三角形三个角的平分线相交于一点. 你想证明这个命题吗?
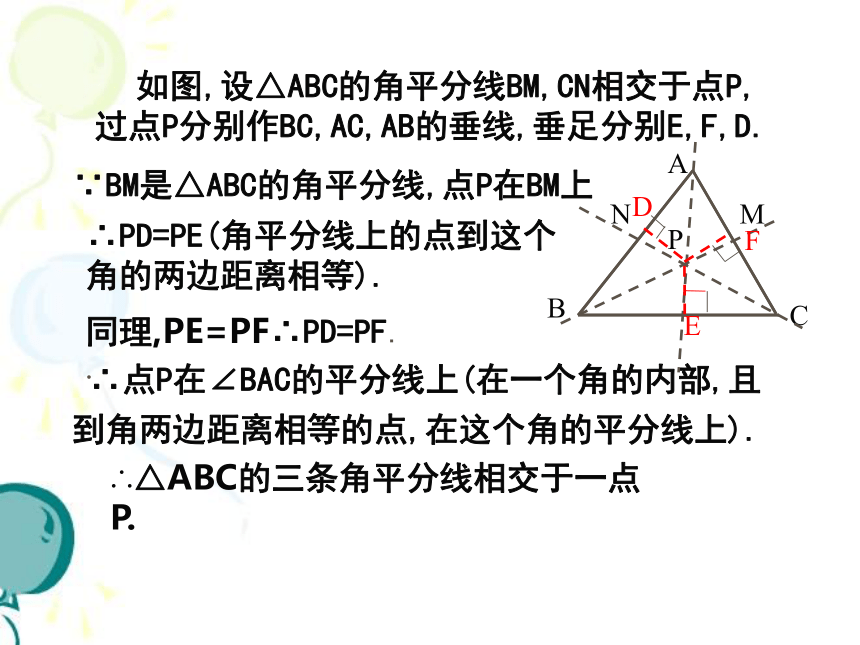
观察这三条角平分线,你发现了什么? 你能证明这个命题吗? 利用尺规作出三角形三个角的角平分线. 结论:三角形三个角的角平分线相交于一点.老师期望:你能写出规范的证明过程.你想证明这个命题吗?你能证明这个命题吗? 再观察这三条角平分线,你又发现了什么?与同伴交流. 命题:三角形三个角的平分线相交于一点. 基本思路:我们知道,两条直线相交只有一个交点.要想证明三条直线相交于一点,只要能证明两条直线的交点在第三条直线上即可.这时可以考 虑前面刚刚学到的逆定理.如何证三条直线交于一点? 如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作BC,AC,AB的垂线,垂足分别E,F,D.∵BM是△ABC的角平分线,点P在BM上∴PD=PE(角平分线上的点到这个角的两边距离相等).同理,PE=PF∴PD=PF.
. ∴点P在∠BAC的平分线上(在一个角的内部,且 到角两边距离相等的点,在这个角的平分线上).∴△ABC的三条角平分线相交于一点P. 定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等. 如图,在△ABC中,
∵BM,CN,AH分别是△ABC的三条角平分且PD⊥AB,PE⊥BC,PF⊥AC 老师提示:这又是一个证明三条直线交于一点的根据之一这个交点叫做三角形的内心.∴BM,CN,AH相交于一点P,且PD=PE=PF(三角形的三条角平分线相交于一点,并且这一点到三边的距离相等).H[例3]如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4 cm,求AC的长;
(2)求证:AB=AC+CD. 练一练(1)解:∵AD是△ABC的角平分线,∠C=90°,DE⊥AB
∴DE=CD=4cm
∵AC=BC ∴∠B=∠BAC(等边对等角)
∵∠C=90°,∴∠B= ×90°=45°.
∴∠BDE=90°-45°=45°.
∴BE=DE(等角对等边).
在等腰直角三角形BDE中
(勾股定理),
∴AC=BC=CD+BD=(4+ )cm.[例3]如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4 cm,求AC的长;
(2)求证:AB=AC+CD. 练一练(2)证明:由(1)的求解过程可知,
Rt△ACD≌Rt△AED(HL)
∴AC=AE(全等三角形的对应边相等)
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
三 挑战自我 1.已知:如图,∠C=900, ∠B=300, AD是Rt△ABC的角平分线.
求证:BD=2CD. 老师期望:你能写出规范的证明过程.证明 ∵ ∠C=90°∴ ∠B= 30°
∴Rt△ABC中,AB=2BC, ∠BAC= 60°
∵ AD是△ABC的角平分线
∴ ∠BAD= ∠DAC= 30°,AD=BD
∴ Rt△ACD中,AD=2CD
∴ BD=2CD
2.已知:如图,△ABC的外角∠CBD和∠BCE的角平分线相交于点F.
求证:点F在∠DAE的平分线上. 证明: ∵ BF是∠CBD的角平分线
∴ F到BC,AD的距离相等
∵ BF是∠CBD的角平分线
∴ F到BC,AE的距离相等
∴ F到AD,AE的距离相等
从而点F在∠DAE的平分线上. 3.已知:如图,P是∠AOB平分线上的一个点,并且PC⊥OA,PD⊥OB,垂足分别是C,D.
求证:
(1)OC=OD;
(2)OP是CD的垂直平分线. BAPDCO证明(1) ∵P为P是∠AOB平分线上的一个点
PC⊥OA,PD⊥OB
∴PC=PD
Rt△POC和 Rt△POD
∵ OP=OP
Rt△POC ≌ Rt△POD ∴OC=OD
(2) 由PC=PD得P在CD的垂直平分线上
由OC=OD得O在CD的垂直平分线上
∴OP是CD的垂直平分线.
拓展探索:如图,已知△ABC,作△ABC一个内角和与它不相邻的两个外角的平分线,看它们是否交于一点?这样的点有几个?如果以这个点为圆心,这一点到三角形一边的距离为半径作圆,你能作出这个图形吗?
四 回顾与小结 定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等(这个交点叫做三角形的内心).
如图,在△ABC中,
∵BM,CN,AH分别是△ABC的三条角平分且PD⊥AB,PE⊥BC,PF⊥AC 老师提示:这又是一个证明三条直线交于一点的根据之一这个交点叫做三角形的内心.∴BM,CN,AH相交于一点P,且PD=PE=PF(三角形的三条角平分线相交于一点,并且这一点到三边的距离相等).H复习题 4,6,7题.
祝你成功! 结束寄语 严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
一 回顾与思考
定理 角平分线上的点到这个角的两边距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.如图,
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等). 逆定理 在一个角的内部,且到角的两边距离 相等的点,在这个角的平分线上.如图,
∵PD=PE, PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).老师提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
二 探究新知 剪一个三角形纸片通过折叠找出每个角的平分线. 结论:三角形三个角的平分线相交于一点. 你想证明这个命题吗?
观察这三条角平分线,你发现了什么? 你能证明这个命题吗? 利用尺规作出三角形三个角的角平分线. 结论:三角形三个角的角平分线相交于一点.老师期望:你能写出规范的证明过程.你想证明这个命题吗?你能证明这个命题吗? 再观察这三条角平分线,你又发现了什么?与同伴交流. 命题:三角形三个角的平分线相交于一点. 基本思路:我们知道,两条直线相交只有一个交点.要想证明三条直线相交于一点,只要能证明两条直线的交点在第三条直线上即可.这时可以考 虑前面刚刚学到的逆定理.如何证三条直线交于一点? 如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作BC,AC,AB的垂线,垂足分别E,F,D.∵BM是△ABC的角平分线,点P在BM上∴PD=PE(角平分线上的点到这个角的两边距离相等).同理,PE=PF∴PD=PF.
. ∴点P在∠BAC的平分线上(在一个角的内部,且 到角两边距离相等的点,在这个角的平分线上).∴△ABC的三条角平分线相交于一点P. 定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等. 如图,在△ABC中,
∵BM,CN,AH分别是△ABC的三条角平分且PD⊥AB,PE⊥BC,PF⊥AC 老师提示:这又是一个证明三条直线交于一点的根据之一这个交点叫做三角形的内心.∴BM,CN,AH相交于一点P,且PD=PE=PF(三角形的三条角平分线相交于一点,并且这一点到三边的距离相等).H[例3]如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4 cm,求AC的长;
(2)求证:AB=AC+CD. 练一练(1)解:∵AD是△ABC的角平分线,∠C=90°,DE⊥AB
∴DE=CD=4cm
∵AC=BC ∴∠B=∠BAC(等边对等角)
∵∠C=90°,∴∠B= ×90°=45°.
∴∠BDE=90°-45°=45°.
∴BE=DE(等角对等边).
在等腰直角三角形BDE中
(勾股定理),
∴AC=BC=CD+BD=(4+ )cm.[例3]如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4 cm,求AC的长;
(2)求证:AB=AC+CD. 练一练(2)证明:由(1)的求解过程可知,
Rt△ACD≌Rt△AED(HL)
∴AC=AE(全等三角形的对应边相等)
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
三 挑战自我 1.已知:如图,∠C=900, ∠B=300, AD是Rt△ABC的角平分线.
求证:BD=2CD. 老师期望:你能写出规范的证明过程.证明 ∵ ∠C=90°∴ ∠B= 30°
∴Rt△ABC中,AB=2BC, ∠BAC= 60°
∵ AD是△ABC的角平分线
∴ ∠BAD= ∠DAC= 30°,AD=BD
∴ Rt△ACD中,AD=2CD
∴ BD=2CD
2.已知:如图,△ABC的外角∠CBD和∠BCE的角平分线相交于点F.
求证:点F在∠DAE的平分线上. 证明: ∵ BF是∠CBD的角平分线
∴ F到BC,AD的距离相等
∵ BF是∠CBD的角平分线
∴ F到BC,AE的距离相等
∴ F到AD,AE的距离相等
从而点F在∠DAE的平分线上. 3.已知:如图,P是∠AOB平分线上的一个点,并且PC⊥OA,PD⊥OB,垂足分别是C,D.
求证:
(1)OC=OD;
(2)OP是CD的垂直平分线. BAPDCO证明(1) ∵P为P是∠AOB平分线上的一个点
PC⊥OA,PD⊥OB
∴PC=PD
Rt△POC和 Rt△POD
∵ OP=OP
Rt△POC ≌ Rt△POD ∴OC=OD
(2) 由PC=PD得P在CD的垂直平分线上
由OC=OD得O在CD的垂直平分线上
∴OP是CD的垂直平分线.
拓展探索:如图,已知△ABC,作△ABC一个内角和与它不相邻的两个外角的平分线,看它们是否交于一点?这样的点有几个?如果以这个点为圆心,这一点到三角形一边的距离为半径作圆,你能作出这个图形吗?
四 回顾与小结 定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等(这个交点叫做三角形的内心).
如图,在△ABC中,
∵BM,CN,AH分别是△ABC的三条角平分且PD⊥AB,PE⊥BC,PF⊥AC 老师提示:这又是一个证明三条直线交于一点的根据之一这个交点叫做三角形的内心.∴BM,CN,AH相交于一点P,且PD=PE=PF(三角形的三条角平分线相交于一点,并且这一点到三边的距离相等).H复习题 4,6,7题.
祝你成功! 结束寄语 严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
