2018_2019学年高中数学第二章函数2.1.2函数的表示方法课件新人教B版必修1(37张)
文档属性
| 名称 | 2018_2019学年高中数学第二章函数2.1.2函数的表示方法课件新人教B版必修1(37张) |

|
|
| 格式 | zip | ||
| 文件大小 | 853.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 00:00:00 | ||
图片预览










文档简介
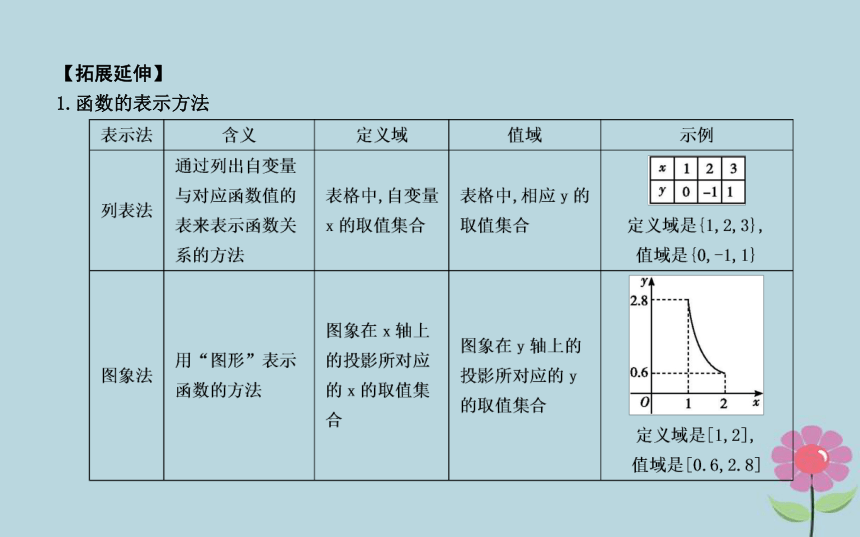
课件37张PPT。2.1.2 函数的表示方法目标导航新知探求课堂探究新知探求·素养养成点击进入 情境导学知识探究1.函数的表示方法图象2.在函数的定义域内,对于自变量x的不同取值区间,有着 的对应法则,这样的函数通常叫做分段函数. 不同【拓展延伸】
1.函数的表示方法2.关于分段函数的几点说明
(1)分段函数是一个函数而不是几个函数.处理分段函数问题时,首先要确定自变量的数值属于哪一个范围,从而选择相应的对应关系.
(2)分段函数的图象,应根据不同定义域上的解析式分别画出,再将它们组合在一起得到整个分段函数的图象.特别要考虑区间端点是否包含在内,若端点包含在内,则用实心点“·”表示;若端点不包含在内,则用空心圆圈“??”表示.(3)写分段函数的定义域时,要注意区间端点值的取舍,区间端点应不重不漏.分段函数的定义域是各段自变量取值范围的并集,各段定义域的交集是空集.
(4)分段函数的值域是各段函数在相应区间上函数取值集合的并集.
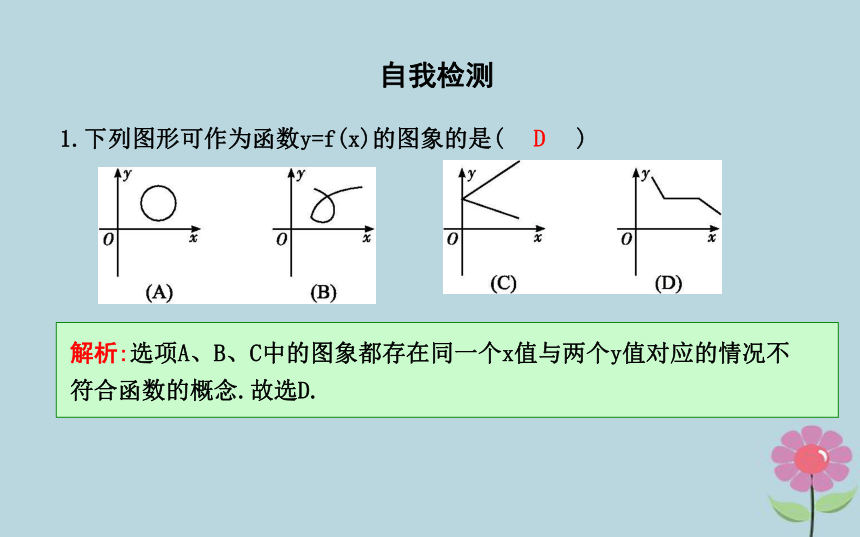
3.分段函数的定义域是各段定义域的并集;分段函数的值域是分别求出各段上的值域后取并集;分段函数的最大(小)值则是分别在每段上求出最大(小)值,然后取各段中的最大(小)值.自我检测1.下列图形可作为函数y=f(x)的图象的是( )D解析:选项A、B、C中的图象都存在同一个x值与两个y值对应的情况不符合函数的概念.故选D.2.已知函数f(x)=x2-3x+1,则f(x-1)的解析式为( )
(A)x2-3x+1 (B)x2-x-1
(C)x2-5x+5 (D)x2-2x+1C解析:因为f(x)=x2-3x+1,所以f(x-1)=(x-1)2-3(x-1)+1=x2-5x+5.选C.A4.某班连续进行了5次数学测试,其中王明的成绩如下表所示:答案:{1,2,3,4,5} {76,84,88,90,91}从这张表中看出这个函数的定义域是 ,值域是 .?类型一 函数的表示方法课堂探究·素养提升解析:由题意f(0)=3,f(f(0))=f(3)=-1,f(f(f(0)))=f(-1)=2.
答案:2方法技巧 用列表法表示的函数,可以直接从表格中寻找自变量对应的函数值及函数值对应的自变量.变式训练1-1:已知函数f(x),g(x)分别由下表给出.则f(g(1))的值为 .?解析:由第2个表知g(1)=3,
所以f(g(1))=f(3)=1.
答案:1变式训练1-2:已知函数y=f(n)满足f(1)=1,f(n+1)=f(n)+2n,n∈N*,求f(2),f(3),f(4).解:因为f(1)=1,
所以f(2)=f(1)+2×1=3,
f(3)=f(2)+2×2=7,
f(4)=f(3)+2×3=13.类型二 作函数的图象【例2】 作出下列函数的图象:
(1)y=1-x(x∈Z且|x|≤2);(2)y=x2-2x-3(x∈R);方法技巧 画函数图象时,以定义域、对应法则为依据,采用列表、描点法作图,当已知是一次式或二次式时,可借助一次函数或二次函数的图象帮助作图.作图象时,应标出某些关键点,如图象的顶点、与坐标轴的交点、最高点、最低点等.要分清这些关键点是实心点还是空心点.(2)y=x2-2x+2,x∈(-1,2];解:(2)x∈(-1,2],图象如图.(3)y=|x-1|,x∈R.解:(3)法一 可用描点作图法,画出函数图象.
法二 可先作出y=x-1的图象,将x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变可得y=|x-1|的图象.如图所示.类型三 分段函数思路点拨:(1)根据自变量的值所在区间选用相应的关系式求值;(2)作出函数的简图;
(3)求函数的值域.思路点拨:(2)分段作出函数的图象;(3)借助图象求函数的值域.
解:(2)在同一坐标系中分段画出函数的图象,如图所示.(3)由图象可知,函数的值域为[0,2]. 方法技巧 分段函数的值域是各段函数值的集合的并集,求值时,一定要注意所给自变量的值所在的范围,代入相应的解析式求得,有多层“f”时,要按照“由里到外”的顺序,画图象时,要注意不同段的图象间的衔接不要出现“一对多”的现象.解:(1)f(-4)=-4+2=-2,f(3)=2×3=6,
f[f(-2)]=f(0)=02=0.
(2)当a≤-1时,a+2=10,得a=8,不符合;
当-1当a≥2时,2a=10,得a=5.所以a=5.类型四 实际应用中的分段函数【例4】 漳州市“网约车”的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元).
(1)将某乘客搭乘一次“网约车”的费用f(x)(单位:元)表示为行程x(060,单位:km)的分段函数;
(2)某乘客的行程为16 km,他准备先乘一辆“网约车”行驶8 km后,再换乘另一辆“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱?请说明理由.思路点拨:根据漳州市“网约车”的计价标准,分段将乘客搭乘一次出租车的费用f(x)(元)表示为行程x(0换乘两辆车的车费为2f(8)=2×(4.2+1.9×8)=38.8(元).
因为40.3>38.8,所以该乘客换乘比只乘一辆车更省钱.方法技巧 由实际问题决定的分段函数,要写出它的解析式,就是根据实际问题需要分成几类就分成几段,求解析式时,先分段分别求出它的解析式,再把各段综合在一起写一个函数.变式训练4-1:为了节约用水,某市打算出台一项水费政策,规定每季度每人用水量不超过5吨时,每吨水的水费为1.2元,若超过5吨而不超过6吨时,超过部分的水费按原价的200%收费,若超过6吨而不超过7吨时,超过部分的水费按原价的400%收费.如果某人本季度实际用水量为x(x≤7)吨,试计算本季度他应交的水费y(单位:元).类型五 易错辨析答案:x2-1.答案:x2-1(x≥1)变式训练5-1:某城市出租车按如下方法收费:起步价6元,可行3 km(含3 km),
3 km后到10 km(含10 km)每走1 km 加价0.5元,10 km后每走1 km加价0.8元,某人坐出租车走了12 km,他应交费 元.?答案:11.1谢谢观赏!
1.函数的表示方法2.关于分段函数的几点说明
(1)分段函数是一个函数而不是几个函数.处理分段函数问题时,首先要确定自变量的数值属于哪一个范围,从而选择相应的对应关系.
(2)分段函数的图象,应根据不同定义域上的解析式分别画出,再将它们组合在一起得到整个分段函数的图象.特别要考虑区间端点是否包含在内,若端点包含在内,则用实心点“·”表示;若端点不包含在内,则用空心圆圈“??”表示.(3)写分段函数的定义域时,要注意区间端点值的取舍,区间端点应不重不漏.分段函数的定义域是各段自变量取值范围的并集,各段定义域的交集是空集.
(4)分段函数的值域是各段函数在相应区间上函数取值集合的并集.
3.分段函数的定义域是各段定义域的并集;分段函数的值域是分别求出各段上的值域后取并集;分段函数的最大(小)值则是分别在每段上求出最大(小)值,然后取各段中的最大(小)值.自我检测1.下列图形可作为函数y=f(x)的图象的是( )D解析:选项A、B、C中的图象都存在同一个x值与两个y值对应的情况不符合函数的概念.故选D.2.已知函数f(x)=x2-3x+1,则f(x-1)的解析式为( )
(A)x2-3x+1 (B)x2-x-1
(C)x2-5x+5 (D)x2-2x+1C解析:因为f(x)=x2-3x+1,所以f(x-1)=(x-1)2-3(x-1)+1=x2-5x+5.选C.A4.某班连续进行了5次数学测试,其中王明的成绩如下表所示:答案:{1,2,3,4,5} {76,84,88,90,91}从这张表中看出这个函数的定义域是 ,值域是 .?类型一 函数的表示方法课堂探究·素养提升解析:由题意f(0)=3,f(f(0))=f(3)=-1,f(f(f(0)))=f(-1)=2.
答案:2方法技巧 用列表法表示的函数,可以直接从表格中寻找自变量对应的函数值及函数值对应的自变量.变式训练1-1:已知函数f(x),g(x)分别由下表给出.则f(g(1))的值为 .?解析:由第2个表知g(1)=3,
所以f(g(1))=f(3)=1.
答案:1变式训练1-2:已知函数y=f(n)满足f(1)=1,f(n+1)=f(n)+2n,n∈N*,求f(2),f(3),f(4).解:因为f(1)=1,
所以f(2)=f(1)+2×1=3,
f(3)=f(2)+2×2=7,
f(4)=f(3)+2×3=13.类型二 作函数的图象【例2】 作出下列函数的图象:
(1)y=1-x(x∈Z且|x|≤2);(2)y=x2-2x-3(x∈R);方法技巧 画函数图象时,以定义域、对应法则为依据,采用列表、描点法作图,当已知是一次式或二次式时,可借助一次函数或二次函数的图象帮助作图.作图象时,应标出某些关键点,如图象的顶点、与坐标轴的交点、最高点、最低点等.要分清这些关键点是实心点还是空心点.(2)y=x2-2x+2,x∈(-1,2];解:(2)x∈(-1,2],图象如图.(3)y=|x-1|,x∈R.解:(3)法一 可用描点作图法,画出函数图象.
法二 可先作出y=x-1的图象,将x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变可得y=|x-1|的图象.如图所示.类型三 分段函数思路点拨:(1)根据自变量的值所在区间选用相应的关系式求值;(2)作出函数的简图;
(3)求函数的值域.思路点拨:(2)分段作出函数的图象;(3)借助图象求函数的值域.
解:(2)在同一坐标系中分段画出函数的图象,如图所示.(3)由图象可知,函数的值域为[0,2]. 方法技巧 分段函数的值域是各段函数值的集合的并集,求值时,一定要注意所给自变量的值所在的范围,代入相应的解析式求得,有多层“f”时,要按照“由里到外”的顺序,画图象时,要注意不同段的图象间的衔接不要出现“一对多”的现象.解:(1)f(-4)=-4+2=-2,f(3)=2×3=6,
f[f(-2)]=f(0)=02=0.
(2)当a≤-1时,a+2=10,得a=8,不符合;
当-1
(1)将某乘客搭乘一次“网约车”的费用f(x)(单位:元)表示为行程x(0
(2)某乘客的行程为16 km,他准备先乘一辆“网约车”行驶8 km后,再换乘另一辆“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱?请说明理由.思路点拨:根据漳州市“网约车”的计价标准,分段将乘客搭乘一次出租车的费用f(x)(元)表示为行程x(0
因为40.3>38.8,所以该乘客换乘比只乘一辆车更省钱.方法技巧 由实际问题决定的分段函数,要写出它的解析式,就是根据实际问题需要分成几类就分成几段,求解析式时,先分段分别求出它的解析式,再把各段综合在一起写一个函数.变式训练4-1:为了节约用水,某市打算出台一项水费政策,规定每季度每人用水量不超过5吨时,每吨水的水费为1.2元,若超过5吨而不超过6吨时,超过部分的水费按原价的200%收费,若超过6吨而不超过7吨时,超过部分的水费按原价的400%收费.如果某人本季度实际用水量为x(x≤7)吨,试计算本季度他应交的水费y(单位:元).类型五 易错辨析答案:x2-1.答案:x2-1(x≥1)变式训练5-1:某城市出租车按如下方法收费:起步价6元,可行3 km(含3 km),
3 km后到10 km(含10 km)每走1 km 加价0.5元,10 km后每走1 km加价0.8元,某人坐出租车走了12 km,他应交费 元.?答案:11.1谢谢观赏!
