2018_2019学年高中数学第三章函数的应用3.2.1几类不同增长的函数模型课件新人教A版必修1(34张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第三章函数的应用3.2.1几类不同增长的函数模型课件新人教A版必修1(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 842.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 00:00:00 | ||
图片预览









文档简介
课件34张PPT。3.2 函数模型及其应用
3.2.1 几类不同增长的函数模型目标导航新知探求课堂探究新知探求·素养养成【情境导学】
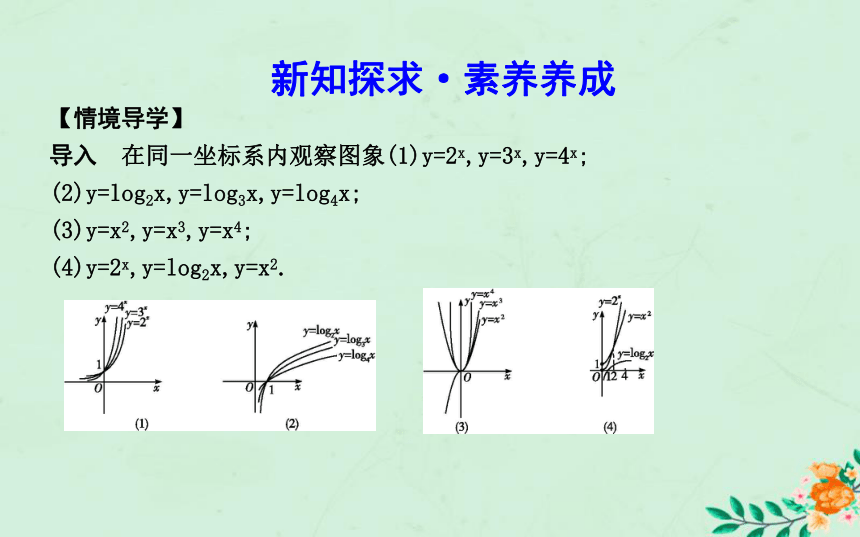
导入 在同一坐标系内观察图象(1)y=2x,y=3x,y=4x;
(2)y=log2x,y=log3x,y=log4x;
(3)y=x2,y=x3,y=x4;
(4)y=2x,y=log2x,y=x2.想一想 指数函数,对数函数底数大于1时增长快慢有什么规律?幂函数的幂指数大于0且不相同时增长快慢如何?
(由图象可知,指数函数在x>0时,底数越大增长得越快,对数函数在x>1时底数越大增长得越慢,幂函数在x>1时指数越大增长得越快)知识探究1.三种函数模型的性质上升上升上升2.三种函数的增长速度比较
(1)在区间(0,+∞)上,函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是
,但 不同,且不在同一个“档次”上.增函数增长速度(2)随着x的增大,y=ax(a>1)增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度 .
(3)存在一个x0,当x>x0时,有 .越来越慢logax三种函数模型的增长差异
(1)指数型函数模型:y=k·ax+b,当k>0,a>1或k<0,0y=k·ax+b,当k>0,01时,在(0,+∞)上为减函数.
(2)对数型函数模型:y=k·logax+b,当k>0,a>1或k<0,0y=k·logax+b,当k>0,01时,在(0,+∞)上为减函数.
(3)幂型函数模型:y=kxn+b,当k>0,n>0时,在(0,+∞)上为增函数;
y=kxn+b,当k<0,n>0时,在(0,+∞)上为减函数.自我检测1.(单调性)下列函数在(0,+∞)上单调递增的是( )C2.(增长速度比较)当x越来越大时,下列函数中,增长速度最快的应该是( )
(A)y=100x (B)y=log100x
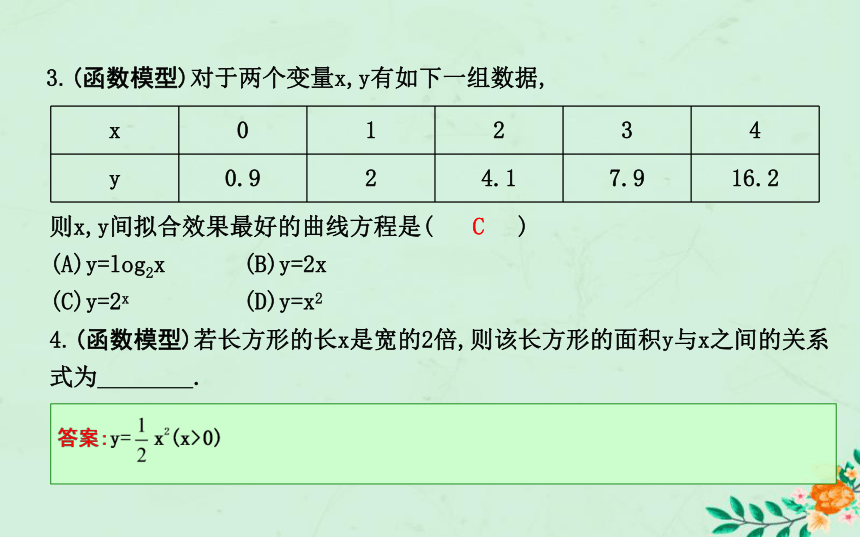
(C)y=x100 (D)y=100xD解析:几种函数模型中,指数函数增长速度最快,故选D.C 3.(函数模型)对于两个变量x,y有如下一组数据,则x,y间拟合效果最好的曲线方程是( )
(A)y=log2x (B)y=2x
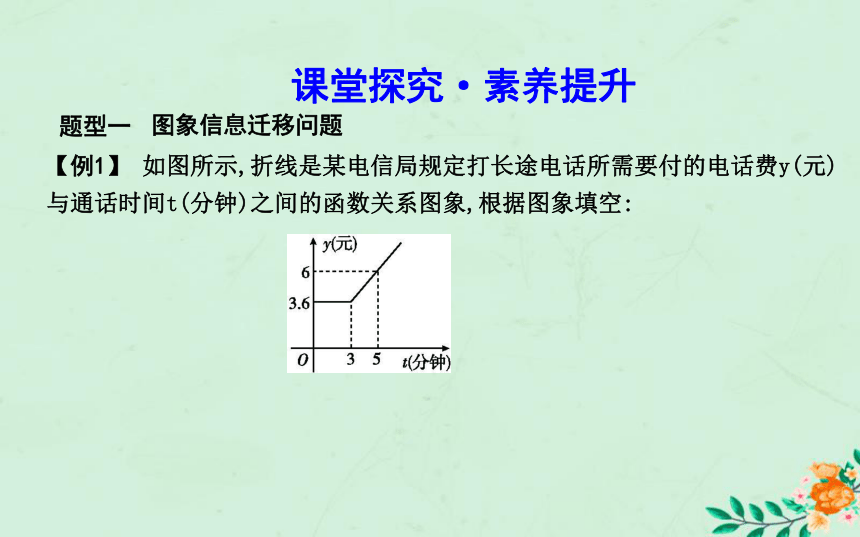
(C)y=2x (D)y=x24.(函数模型)若长方形的长x是宽的2倍,则该长方形的面积y与x之间的关系式为 .?题型一图象信息迁移问题课堂探究·素养提升【例1】 如图所示,折线是某电信局规定打长途电话所需要付的电话费y(元)与通话时间t(分钟)之间的函数关系图象,根据图象填空:解析:(1)由题中图象可知,当0≤t≤3时,电话费都是3.6元.
(2)由题中图象可知,当t=5时,y=6,需付电话费6元.(1)通话2分钟,需付电话费 元;?
(2)通话5分钟,需付电话费 元;?
(3)如果t≥3,则电话费y(元)与通话时间t(分钟)之间的函数关系式为
.?答案:(1)3.6 (2)6 (3)y=1.2t(t≥3)方法技巧 解答图象信息迁移题的方法
(1)明确横轴,纵轴的意义,如本题中横轴t表示通话时间,纵轴y表示电话费;
(2)从图象形状上判定函数模型,如本题中在区间[0,3]和[3,+∞)上均是直线型;
(3)抓住特殊点的实际意义,特殊点一般包括最高点(最大值点)、最低点(最小值点)及折线的拐角点等;
(4)通过方程、不等式、函数等数学模型化实际问题为数学问题.即时训练1-1:某工厂6年来生产某种产品的情况是:前三年年产量的增长速度越来越快,后三年年产量的增长速度保持不变,则可以用来描述该厂前t年这种产品的年产量c与时间t的函数关系的是( )解析:注意以下几种情形:图①表示不再增长,图②表示增速恒定不变,图③表示增长速度越来越快,图④表示增长速度逐渐变慢.故选A.【备用例1】 一天,亮亮发烧了,早晨他烧得很厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么发烫.下列各图中能基本上反映出亮亮这一天(0时~24时)体温的变化情况的是( )解析:观察图象A,体温逐渐降低,不合题意;图象B不能反映“下午体温又开始上升”;图象D不能体现“下午体温又开始上升”与“直到半夜才感觉身上不那么发烫”.故选C.题型二 常见函数模型增长趋势的比较【例2】 函数f(x)=2x和g(x)=x3(x≥0)的图象,如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x11 000,f(10)=1 024,
所以f(1)>g(1),f(2)f(10)>g(10).
所以1所以x1<8从题中图象上知,当x1当x>x2时,f(x)>g(x),且g(x)在(0,+∞)上是增函数,
所以f(2 015)>g(2 015)>g(8)>f(8).方法技巧 由指数函数、对数函数增长的规律识别图象,即指数函数增长的速度越来越快,在某一位置会远远超过幂函数的增长,总存在x0,使x>x0时,ax>xα.即时训练2-1:函数f(x)=lg x,g(x)=0.3x-1的图象如图所示.
(1)指出图中曲线C1,C2分别对应哪一个函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).解:(1)C1对应的函数为g(x)=0.3x-1,
C2对应的函数为f(x)=lg x.
(2)当x∈(0,x1)时,g(x)>f(x),
当x∈(x1,x2)时,g(x)当x∈(x2,+∞)时,g(x)>f(x).题型三 函数模型的选取【例3】 某工厂今年1月、2月、3月生产某种产品分别为1万件、1.2万件、1.3万件,为估测以后每个月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y和月份x的关系,模拟函数可以选用二次函数y=ax2+bx+c或函数y=a·bx+c(其中a,b,c为常数,a≠0,b>0且b≠1).已知4月份该产品的产量为1.37万件,问用上述哪一种函数作为模拟函数好?请说明理由.方法技巧 开放型的探究题,函数模型不是确定的,需要我们去探索,去尝试,找到最合适的模型,解题过程一般为:
(1)用待定系数法求出函数解析式;
(2)检验:将(1)中求出的几个函数模型进行比较、验证,得出最适合的函数模型;
(3)利用所求出的函数模型解决问题.即时训练3-1:某工厂生产一种电脑元件,每月的生产数据如表:为估计以后每月对该电脑元件的产量,以这三个月的产量为依据,用函数y=ax+b或y=ax+b(a,b为常数,且a>0)来模拟这种电脑元件的月产量y千件与月份x的关系.请问:用以上哪个模拟函数较好?说明理由.【备用例2】 某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷、0.76万公顷,则沙漠增加数y(万公顷)关于年数x的函数关系较为近似的是( )题型四建立函数模型解决实际问题【例4】 大西洋鲑鱼每年都要逆流而上,游回产地产卵.记鲑鱼的游速为v(m/s),鲑鱼的耗氧量的单位数为Q,研究中发现v与log3 成正比,且当Q=900时,v=1.
(1)求出v关于Q的函数解析式;(2)计算一条鲑鱼的游速是1.5 m/s时耗氧量的单位数.方法技巧 数学建模中要对所给条件进行简化及合理的假设,从中区分出主要条件及次要条件,再根据要求选取合适的数学知识来求解.即时训练4-1:为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间x(分)与通话费用y(元)的关系如图所示.(1)分别求出通话费用y1,y2与通话时间x之间的函数解析式;(2)请帮助用户计算在一个月内使用哪种卡便宜.题型五 易错辨析——增长趋势把握不准致误【例5】 甲、乙、丙、丁四个物体同时从某一点出发向同一方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,
f2(x)=x2,f3(x)=x,f4(x)=log2(x+1).有以下结论:
①当x>1时,甲走在最前面;
②当x>1时,乙走在最前面;
③当01时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 .?错解:①③⑤
纠错:没有深入研究,单凭主观臆测无根据.正解:四个函数的图象如图所示,根据图象易知,③④⑤正确.答案:③④⑤谢谢观赏!
3.2.1 几类不同增长的函数模型目标导航新知探求课堂探究新知探求·素养养成【情境导学】
导入 在同一坐标系内观察图象(1)y=2x,y=3x,y=4x;
(2)y=log2x,y=log3x,y=log4x;
(3)y=x2,y=x3,y=x4;
(4)y=2x,y=log2x,y=x2.想一想 指数函数,对数函数底数大于1时增长快慢有什么规律?幂函数的幂指数大于0且不相同时增长快慢如何?
(由图象可知,指数函数在x>0时,底数越大增长得越快,对数函数在x>1时底数越大增长得越慢,幂函数在x>1时指数越大增长得越快)知识探究1.三种函数模型的性质上升上升上升2.三种函数的增长速度比较
(1)在区间(0,+∞)上,函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是
,但 不同,且不在同一个“档次”上.增函数增长速度(2)随着x的增大,y=ax(a>1)增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度 .
(3)存在一个x0,当x>x0时,有 .越来越慢logax
(1)指数型函数模型:y=k·ax+b,当k>0,a>1或k<0,0
(2)对数型函数模型:y=k·logax+b,当k>0,a>1或k<0,0
(3)幂型函数模型:y=kxn+b,当k>0,n>0时,在(0,+∞)上为增函数;
y=kxn+b,当k<0,n>0时,在(0,+∞)上为减函数.自我检测1.(单调性)下列函数在(0,+∞)上单调递增的是( )C2.(增长速度比较)当x越来越大时,下列函数中,增长速度最快的应该是( )
(A)y=100x (B)y=log100x
(C)y=x100 (D)y=100xD解析:几种函数模型中,指数函数增长速度最快,故选D.C 3.(函数模型)对于两个变量x,y有如下一组数据,则x,y间拟合效果最好的曲线方程是( )
(A)y=log2x (B)y=2x
(C)y=2x (D)y=x24.(函数模型)若长方形的长x是宽的2倍,则该长方形的面积y与x之间的关系式为 .?题型一图象信息迁移问题课堂探究·素养提升【例1】 如图所示,折线是某电信局规定打长途电话所需要付的电话费y(元)与通话时间t(分钟)之间的函数关系图象,根据图象填空:解析:(1)由题中图象可知,当0≤t≤3时,电话费都是3.6元.
(2)由题中图象可知,当t=5时,y=6,需付电话费6元.(1)通话2分钟,需付电话费 元;?
(2)通话5分钟,需付电话费 元;?
(3)如果t≥3,则电话费y(元)与通话时间t(分钟)之间的函数关系式为
.?答案:(1)3.6 (2)6 (3)y=1.2t(t≥3)方法技巧 解答图象信息迁移题的方法
(1)明确横轴,纵轴的意义,如本题中横轴t表示通话时间,纵轴y表示电话费;
(2)从图象形状上判定函数模型,如本题中在区间[0,3]和[3,+∞)上均是直线型;
(3)抓住特殊点的实际意义,特殊点一般包括最高点(最大值点)、最低点(最小值点)及折线的拐角点等;
(4)通过方程、不等式、函数等数学模型化实际问题为数学问题.即时训练1-1:某工厂6年来生产某种产品的情况是:前三年年产量的增长速度越来越快,后三年年产量的增长速度保持不变,则可以用来描述该厂前t年这种产品的年产量c与时间t的函数关系的是( )解析:注意以下几种情形:图①表示不再增长,图②表示增速恒定不变,图③表示增长速度越来越快,图④表示增长速度逐渐变慢.故选A.【备用例1】 一天,亮亮发烧了,早晨他烧得很厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么发烫.下列各图中能基本上反映出亮亮这一天(0时~24时)体温的变化情况的是( )解析:观察图象A,体温逐渐降低,不合题意;图象B不能反映“下午体温又开始上升”;图象D不能体现“下午体温又开始上升”与“直到半夜才感觉身上不那么发烫”.故选C.题型二 常见函数模型增长趋势的比较【例2】 函数f(x)=2x和g(x)=x3(x≥0)的图象,如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1
所以f(1)>g(1),f(2)
所以1
所以f(2 015)>g(2 015)>g(8)>f(8).方法技巧 由指数函数、对数函数增长的规律识别图象,即指数函数增长的速度越来越快,在某一位置会远远超过幂函数的增长,总存在x0,使x>x0时,ax>xα.即时训练2-1:函数f(x)=lg x,g(x)=0.3x-1的图象如图所示.
(1)指出图中曲线C1,C2分别对应哪一个函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).解:(1)C1对应的函数为g(x)=0.3x-1,
C2对应的函数为f(x)=lg x.
(2)当x∈(0,x1)时,g(x)>f(x),
当x∈(x1,x2)时,g(x)
(1)用待定系数法求出函数解析式;
(2)检验:将(1)中求出的几个函数模型进行比较、验证,得出最适合的函数模型;
(3)利用所求出的函数模型解决问题.即时训练3-1:某工厂生产一种电脑元件,每月的生产数据如表:为估计以后每月对该电脑元件的产量,以这三个月的产量为依据,用函数y=ax+b或y=ax+b(a,b为常数,且a>0)来模拟这种电脑元件的月产量y千件与月份x的关系.请问:用以上哪个模拟函数较好?说明理由.【备用例2】 某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷、0.76万公顷,则沙漠增加数y(万公顷)关于年数x的函数关系较为近似的是( )题型四建立函数模型解决实际问题【例4】 大西洋鲑鱼每年都要逆流而上,游回产地产卵.记鲑鱼的游速为v(m/s),鲑鱼的耗氧量的单位数为Q,研究中发现v与log3 成正比,且当Q=900时,v=1.
(1)求出v关于Q的函数解析式;(2)计算一条鲑鱼的游速是1.5 m/s时耗氧量的单位数.方法技巧 数学建模中要对所给条件进行简化及合理的假设,从中区分出主要条件及次要条件,再根据要求选取合适的数学知识来求解.即时训练4-1:为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间x(分)与通话费用y(元)的关系如图所示.(1)分别求出通话费用y1,y2与通话时间x之间的函数解析式;(2)请帮助用户计算在一个月内使用哪种卡便宜.题型五 易错辨析——增长趋势把握不准致误【例5】 甲、乙、丙、丁四个物体同时从某一点出发向同一方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,
f2(x)=x2,f3(x)=x,f4(x)=log2(x+1).有以下结论:
①当x>1时,甲走在最前面;
②当x>1时,乙走在最前面;
③当0
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 .?错解:①③⑤
纠错:没有深入研究,单凭主观臆测无根据.正解:四个函数的图象如图所示,根据图象易知,③④⑤正确.答案:③④⑤谢谢观赏!
