人教版七年级下册5.3《平行线的性质》同步测试题(含答案)
文档属性
| 名称 | 人教版七年级下册5.3《平行线的性质》同步测试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 86.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 00:00:00 | ||
图片预览


文档简介
人教版七年级下册5.3《平行线的性质》测试
选择题
1、下列图形中,由,能得到的是????????????? ( ??)
2、若两条平行线被第三条直线所截,则一组同位角的平分线互相( )
A.垂直????? B.平行????? C.重合????? D.相交
3、下列命题正确的是
A.两直线与第三条直线相交,同位角相等
B.两直线与第三条直线相交,内错角相等
C.两直线平行,同旁内角相等
D.两直线平行,内错角相等
4、已知AB∥CD,直线EF分别交AB,CD于点G,H,∠EGB=25°,将一个含有60°角的直角三角尺如图放置(60°角的顶点与H重合),则∠PHG等于( )
A.30°? B.35°? C.40°? D.45°
5、如图,直线a∥b,直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是(???? )
A.50°? B.70°? C.80°? D.110°
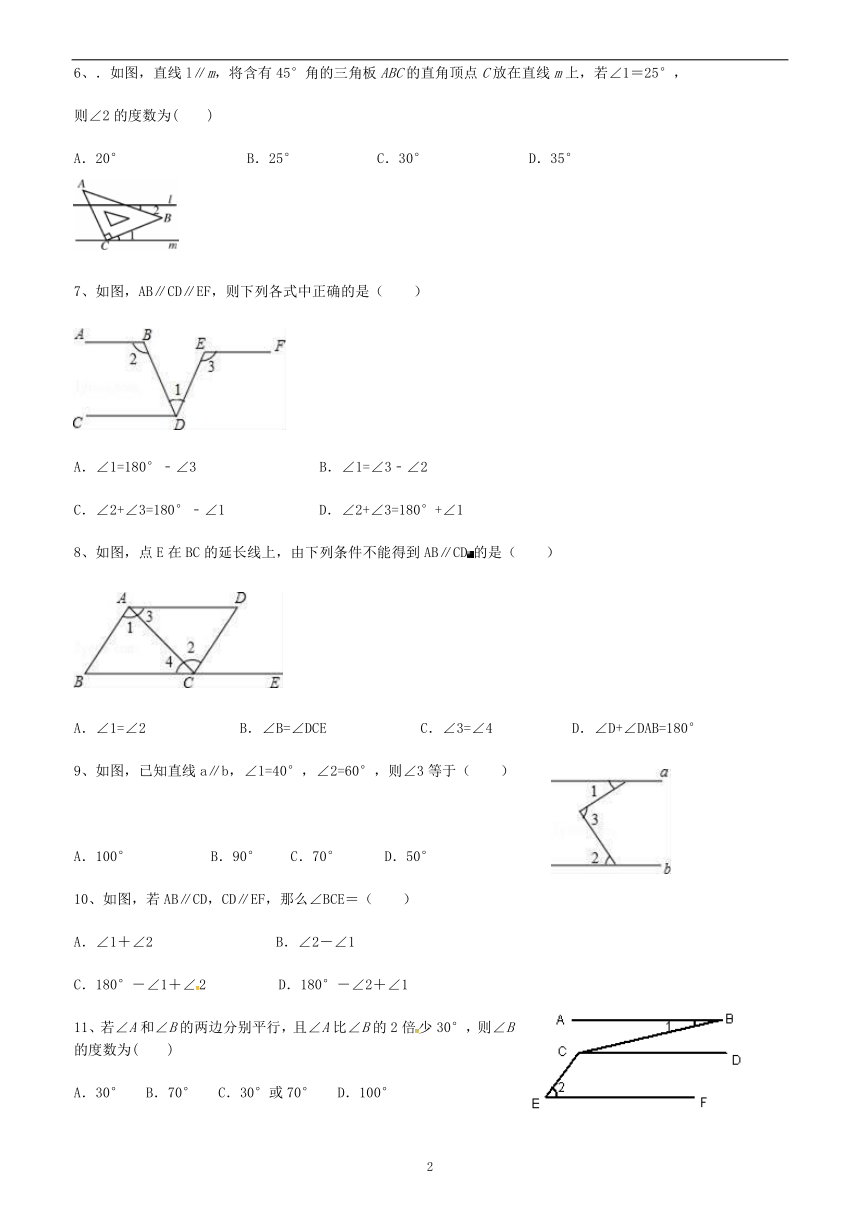
6、.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,
则∠2的度数为( )
A.20°???????? B.25° ?????C.30° ?????? D.35°
7、如图,AB∥CD∥EF,则下列各式中正确的是( )
A.∠1=180°﹣∠3 B.∠1=∠3﹣∠2
C.∠2+∠3=180°﹣∠1?????? D.∠2+∠3=180°+∠1
8、如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是( )
A.∠1=∠2?????? B.∠B=∠DCE?????? C.∠3=∠4????? D.∠D+∠DAB=180°
9、如图,已知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
A.100°????? B.90° C.70° D.50°
10、如图,若AB∥CD,CD∥EF,那么∠BCE=( )
A.∠1+∠2???????? B.∠2-∠1
C.180°-∠1+∠2? ??? D.180°-∠2+∠1
11、若∠A和∠B的两边分别平行,且∠A比∠B的2倍少30°,则∠B的度数为( )
A.30°? B.70°? C.30°或70°? D.100°
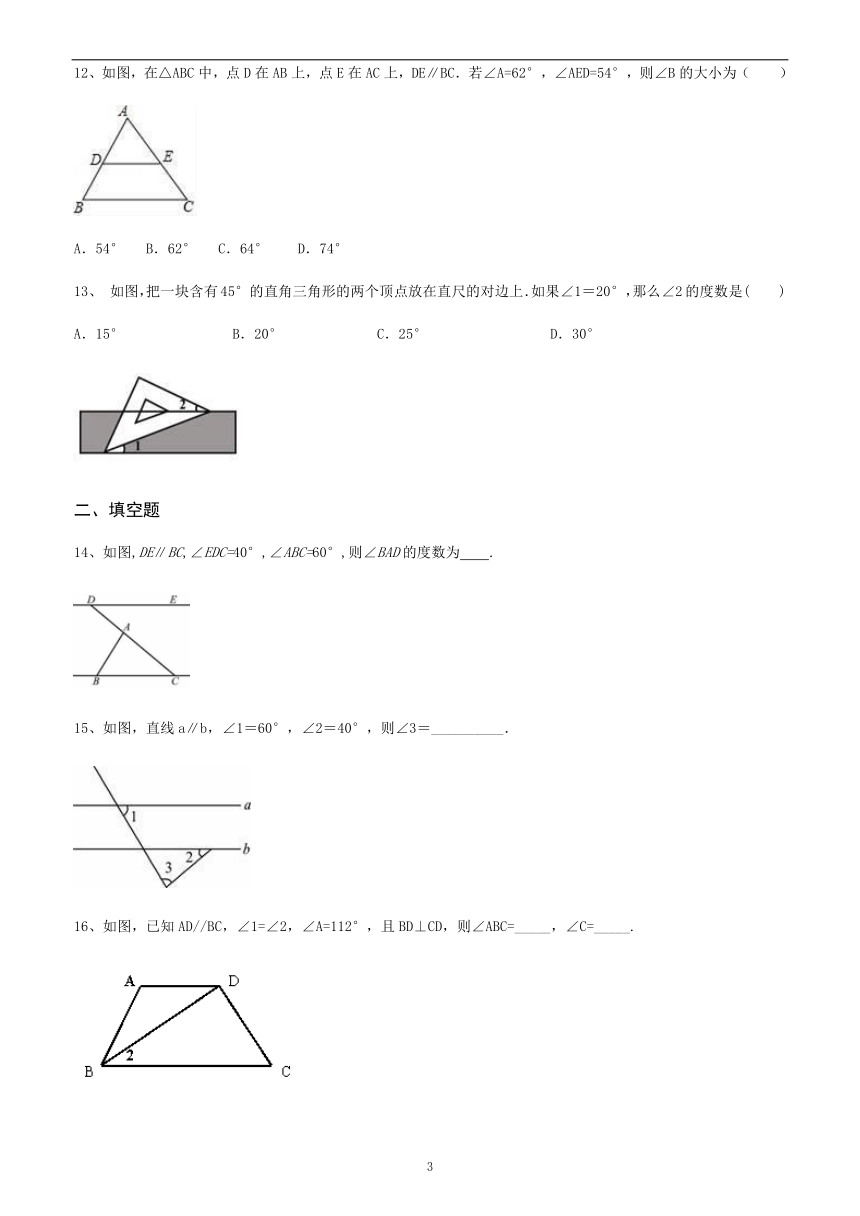
12、如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )
A.54° B.62° C.64° D.74°
13、?如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A.15°??????? B.20°?????? C.25°???????? D.30°
二、填空题
14、如图,DE∥BC,∠EDC=40°,∠ABC=60°,则∠BAD的度数为 .?
15、如图,直线a∥b,∠1=60°,∠2=40°,则∠3=__________.
16、如图,已知AD//BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=_____,∠C=_____.?
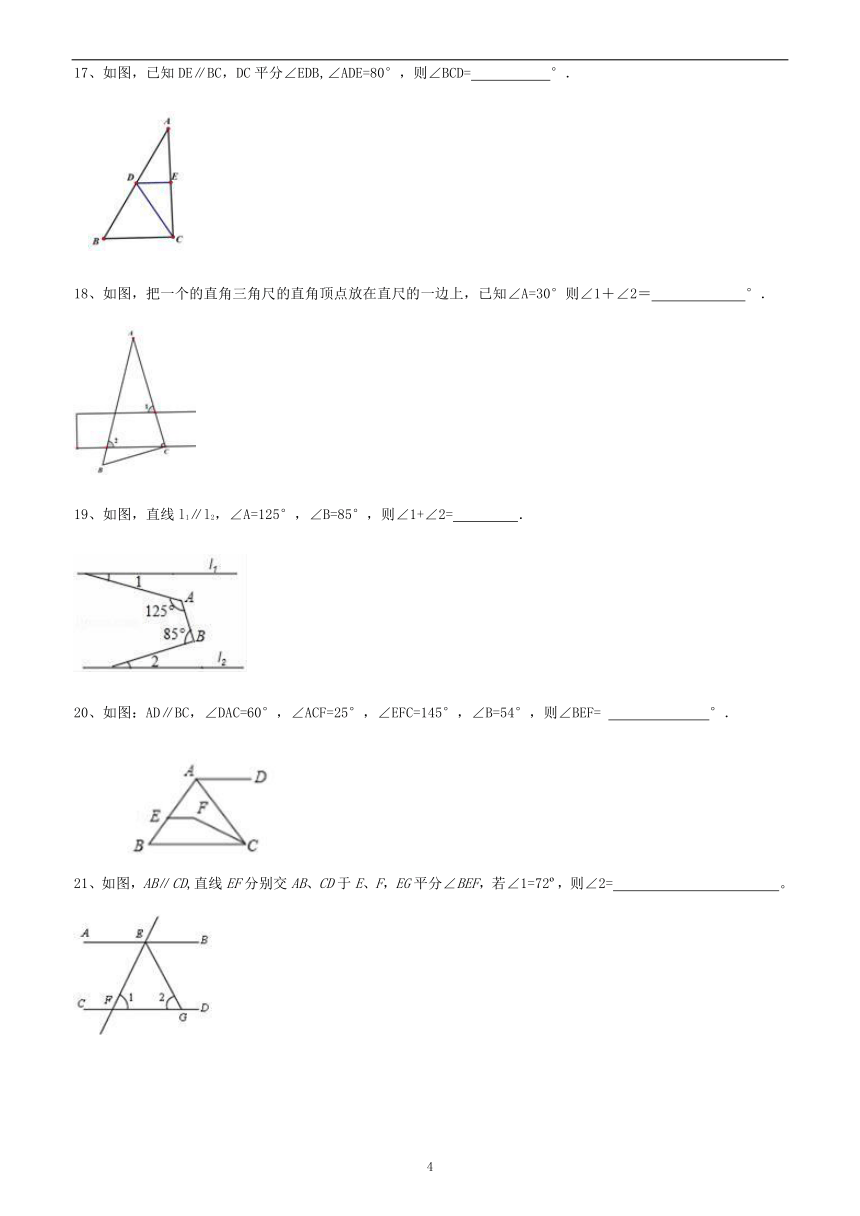
17、如图,已知DE∥BC,DC平分∠EDB,∠ADE=80°,则∠BCD=? ????°.
?
18、如图,把一个的直角三角尺的直角顶点放在直尺的一边上,已知∠A=30°则∠1+∠2=?? ????°.
?
19、如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2= ?? .
20、如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF= ???????°.
21、如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72o,则∠2=??????????? 。
?
22、如图,把长方形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF=________.
23、、如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,
??? ∠1=50°,则∠2等于????????
24、如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=35o,
那么∠2=????? 度.
25、下列命题中:
①若,则;??????②两直线平行,同位角相等;
③对顶角相等;?????? ????④内错角相等,两直线平行.
是真命题的是?????? ?.(填写所有真命题的序号)
三、简答题
26、根据逻辑填空:如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.
解:∠B+∠E=∠BCE,过点C作CF∥AB,
则???? (??????????????????????????? )
又∵AB∥DE,AB∥CF,
∴____________( ???????????????????????????)
∴∠E=∠???? ( )
∴∠B+∠E=∠1+∠2,即∠B+∠E=∠BCE.
27、如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
28、如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
29、将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB
(2)求∠DFC的度数.
30、如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F. 已知EG∥AD交BC于G, EH⊥BE交BC于H,∠HEG = 50°.
(1)求∠BFD的度数.
(2)若∠BAD = ∠EBC,∠C = 41°,求∠BAC的度数.
参考答案
一、选择题
1、B
2、B已知:AB∥CD,PM与QN分别平分∠EMB与∠MND.
求证:PM∥QN.
证明:∵AB∥CD,
∴∠EMB=∠MND,
∵PM与QN分别平分∠EMB与∠MND,
∴∠1=∠EMB,∠2=∠MND,
∴∠1=∠2,
∴PM∥QN.
故选:B.
3、d
4、B
5、C
6、A
7、D【解答】解:∵AB∥CD,
∴∠2+∠BDC=180°,即∠BDC=180°﹣∠2,
∵EF∥CD,
∴∠BDC+∠1=∠3,即∠BDC=∠3﹣∠1,
∴180°﹣∠2=∠3﹣∠1,即∠2+∠3=180°+∠1,
8、C【解答】解:A、正确,符合内错角相等,两条直线平行的判定定理;
B、正确,符合同位角相等,两条直线平行的判定定理;
C、错误,若∠3=∠4,则AD∥BE;
D、正确,符合同旁内角互补,两条直线平行的判定定理;
9、A【解答】解:过点C作CD∥a,
∵a∥b,
∴CD∥a∥b,
∴∠ACD=∠1=40°,∠BCD=∠2=60°,
∴∠3=∠ACD+∠BCD=100°.
故选:A.
10、D
11、C
12、C解:∵DE∥BC,
∴∠C=∠AED=54°,
∵∠A=62°,
∴∠B=180°﹣∠A﹣∠C=64°,
13、C???
二、填空题
14、100°
15、80°
16、
17、50°
18、150 ?
19、30° .
?【分析】先利用三角形外角性质得∠1+∠3=125°,∠2+∠4=85°,把两式相加得到∠1+∠3+∠2+∠4=210°,再根据平行线的性质,由l1∥l2得到∠3+∠4=180°,然后通过角度的计算得到∠1+∠2的度数.
【解答】解:如图,
∵∠1+∠3=125°,∠2+∠4=85°,
∴∠1+∠3+∠2+∠4=210°,
∵l1∥l2,
∴∠3+∠4=180°,
∴∠1+∠2=210°﹣180°=30°.
故答案为30°.
20、126
21、54°
22、115°
23、
24、、110°、
25、②③④???
三、简答题
26、解:∠B+∠E=∠BCE,过点C作CF∥AB,
则∠B=∠? 1?? ( 两直线平行,内错角相等? )
又∵AB∥DE,AB∥CF,
∴?? DE∥CF?? (? 平行于同一条直线的两条直线平行?? )
∴∠E=∠?? 2? ( 两直线平行,内错角相等 )
∴∠B+∠E=∠1+∠2,即∠B+∠E=∠BCE.
27、解:(1)55°
(2)∠1+∠2=∠3.理由如下:
∵l1∥l2,∴∠1+∠PCD+∠PDC+∠2=180°.
在三角形PCD中,∠3+∠PCD+∠PDC=180°,
∴∠1+∠2=∠3.
(3)由(2)可知∠BAC=∠DBA+∠ACE=40°+45°=85°.
(4)当P点在A的外侧时,∠3=∠2-∠1;
当P点在B的外侧时,∠3=∠1-∠2.
28、【解答】解:∵AB∥CD,∠B=40°,
∴∠BCE=180°﹣∠B=180°﹣40°=140°,[来源:学科网ZXXK]
∵CN是∠BCE的平分线,
∴∠BCN=∠BCE=×140°=70°,
∵CM⊥CN,
∴∠BCM=20°.
29、【解答】(1)证明:由题意知,△ACB是等腰直角三角形,且∠ACB=∠DCB=90°,
∴∠B=45°.
∵CF平分∠DCE,
∴∠DCF=∠ECF=45°,
∴∠B=∠ECF,
∴CF∥AB.
(2)由三角板知,∠E=60°,
由(1)知,∠ECF=45°,
∵∠DFC=∠ECF+∠E,
∴∠DFC=45°+60°=105°.
30、∠BFD=40°(2)∠BAC=99°
选择题
1、下列图形中,由,能得到的是????????????? ( ??)
2、若两条平行线被第三条直线所截,则一组同位角的平分线互相( )
A.垂直????? B.平行????? C.重合????? D.相交
3、下列命题正确的是
A.两直线与第三条直线相交,同位角相等
B.两直线与第三条直线相交,内错角相等
C.两直线平行,同旁内角相等
D.两直线平行,内错角相等
4、已知AB∥CD,直线EF分别交AB,CD于点G,H,∠EGB=25°,将一个含有60°角的直角三角尺如图放置(60°角的顶点与H重合),则∠PHG等于( )
A.30°? B.35°? C.40°? D.45°
5、如图,直线a∥b,直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是(???? )
A.50°? B.70°? C.80°? D.110°
6、.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,
则∠2的度数为( )
A.20°???????? B.25° ?????C.30° ?????? D.35°
7、如图,AB∥CD∥EF,则下列各式中正确的是( )
A.∠1=180°﹣∠3 B.∠1=∠3﹣∠2
C.∠2+∠3=180°﹣∠1?????? D.∠2+∠3=180°+∠1
8、如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是( )
A.∠1=∠2?????? B.∠B=∠DCE?????? C.∠3=∠4????? D.∠D+∠DAB=180°
9、如图,已知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
A.100°????? B.90° C.70° D.50°
10、如图,若AB∥CD,CD∥EF,那么∠BCE=( )
A.∠1+∠2???????? B.∠2-∠1
C.180°-∠1+∠2? ??? D.180°-∠2+∠1
11、若∠A和∠B的两边分别平行,且∠A比∠B的2倍少30°,则∠B的度数为( )
A.30°? B.70°? C.30°或70°? D.100°
12、如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )
A.54° B.62° C.64° D.74°
13、?如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A.15°??????? B.20°?????? C.25°???????? D.30°
二、填空题
14、如图,DE∥BC,∠EDC=40°,∠ABC=60°,则∠BAD的度数为 .?
15、如图,直线a∥b,∠1=60°,∠2=40°,则∠3=__________.
16、如图,已知AD//BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=_____,∠C=_____.?
17、如图,已知DE∥BC,DC平分∠EDB,∠ADE=80°,则∠BCD=? ????°.
?
18、如图,把一个的直角三角尺的直角顶点放在直尺的一边上,已知∠A=30°则∠1+∠2=?? ????°.
?
19、如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2= ?? .
20、如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF= ???????°.
21、如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72o,则∠2=??????????? 。
?
22、如图,把长方形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF=________.
23、、如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,
??? ∠1=50°,则∠2等于????????
24、如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=35o,
那么∠2=????? 度.
25、下列命题中:
①若,则;??????②两直线平行,同位角相等;
③对顶角相等;?????? ????④内错角相等,两直线平行.
是真命题的是?????? ?.(填写所有真命题的序号)
三、简答题
26、根据逻辑填空:如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.
解:∠B+∠E=∠BCE,过点C作CF∥AB,
则???? (??????????????????????????? )
又∵AB∥DE,AB∥CF,
∴____________( ???????????????????????????)
∴∠E=∠???? ( )
∴∠B+∠E=∠1+∠2,即∠B+∠E=∠BCE.
27、如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
28、如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
29、将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB
(2)求∠DFC的度数.
30、如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F. 已知EG∥AD交BC于G, EH⊥BE交BC于H,∠HEG = 50°.
(1)求∠BFD的度数.
(2)若∠BAD = ∠EBC,∠C = 41°,求∠BAC的度数.
参考答案
一、选择题
1、B
2、B已知:AB∥CD,PM与QN分别平分∠EMB与∠MND.
求证:PM∥QN.
证明:∵AB∥CD,
∴∠EMB=∠MND,
∵PM与QN分别平分∠EMB与∠MND,
∴∠1=∠EMB,∠2=∠MND,
∴∠1=∠2,
∴PM∥QN.
故选:B.
3、d
4、B
5、C
6、A
7、D【解答】解:∵AB∥CD,
∴∠2+∠BDC=180°,即∠BDC=180°﹣∠2,
∵EF∥CD,
∴∠BDC+∠1=∠3,即∠BDC=∠3﹣∠1,
∴180°﹣∠2=∠3﹣∠1,即∠2+∠3=180°+∠1,
8、C【解答】解:A、正确,符合内错角相等,两条直线平行的判定定理;
B、正确,符合同位角相等,两条直线平行的判定定理;
C、错误,若∠3=∠4,则AD∥BE;
D、正确,符合同旁内角互补,两条直线平行的判定定理;
9、A【解答】解:过点C作CD∥a,
∵a∥b,
∴CD∥a∥b,
∴∠ACD=∠1=40°,∠BCD=∠2=60°,
∴∠3=∠ACD+∠BCD=100°.
故选:A.
10、D
11、C
12、C解:∵DE∥BC,
∴∠C=∠AED=54°,
∵∠A=62°,
∴∠B=180°﹣∠A﹣∠C=64°,
13、C???
二、填空题
14、100°
15、80°
16、
17、50°
18、150 ?
19、30° .
?【分析】先利用三角形外角性质得∠1+∠3=125°,∠2+∠4=85°,把两式相加得到∠1+∠3+∠2+∠4=210°,再根据平行线的性质,由l1∥l2得到∠3+∠4=180°,然后通过角度的计算得到∠1+∠2的度数.
【解答】解:如图,
∵∠1+∠3=125°,∠2+∠4=85°,
∴∠1+∠3+∠2+∠4=210°,
∵l1∥l2,
∴∠3+∠4=180°,
∴∠1+∠2=210°﹣180°=30°.
故答案为30°.
20、126
21、54°
22、115°
23、
24、、110°、
25、②③④???
三、简答题
26、解:∠B+∠E=∠BCE,过点C作CF∥AB,
则∠B=∠? 1?? ( 两直线平行,内错角相等? )
又∵AB∥DE,AB∥CF,
∴?? DE∥CF?? (? 平行于同一条直线的两条直线平行?? )
∴∠E=∠?? 2? ( 两直线平行,内错角相等 )
∴∠B+∠E=∠1+∠2,即∠B+∠E=∠BCE.
27、解:(1)55°
(2)∠1+∠2=∠3.理由如下:
∵l1∥l2,∴∠1+∠PCD+∠PDC+∠2=180°.
在三角形PCD中,∠3+∠PCD+∠PDC=180°,
∴∠1+∠2=∠3.
(3)由(2)可知∠BAC=∠DBA+∠ACE=40°+45°=85°.
(4)当P点在A的外侧时,∠3=∠2-∠1;
当P点在B的外侧时,∠3=∠1-∠2.
28、【解答】解:∵AB∥CD,∠B=40°,
∴∠BCE=180°﹣∠B=180°﹣40°=140°,[来源:学科网ZXXK]
∵CN是∠BCE的平分线,
∴∠BCN=∠BCE=×140°=70°,
∵CM⊥CN,
∴∠BCM=20°.
29、【解答】(1)证明:由题意知,△ACB是等腰直角三角形,且∠ACB=∠DCB=90°,
∴∠B=45°.
∵CF平分∠DCE,
∴∠DCF=∠ECF=45°,
∴∠B=∠ECF,
∴CF∥AB.
(2)由三角板知,∠E=60°,
由(1)知,∠ECF=45°,
∵∠DFC=∠ECF+∠E,
∴∠DFC=45°+60°=105°.
30、∠BFD=40°(2)∠BAC=99°
