人教版七年级下册 第五章 相交线与平行线5.2.2 平行线的判定(34张PPT)
文档属性
| 名称 | 人教版七年级下册 第五章 相交线与平行线5.2.2 平行线的判定(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 561.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 00:00:00 | ||
图片预览





文档简介
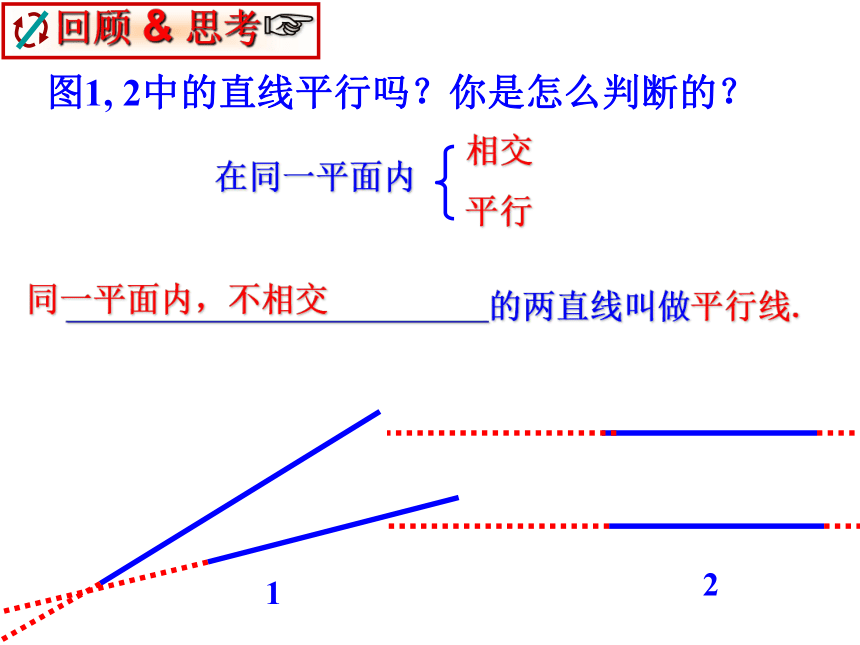
课件34张PPT。5.2.2 平行线的判定回顾与思考在同一平面内相交平行 的两直线叫做平行线.同一平面内,不相交图1, 2中的直线平行吗?你是怎么判断的?12判定两条直线平行的方法有两种:定义:在同一平面内,不相交的两条直线叫平行线。同学们想一想:
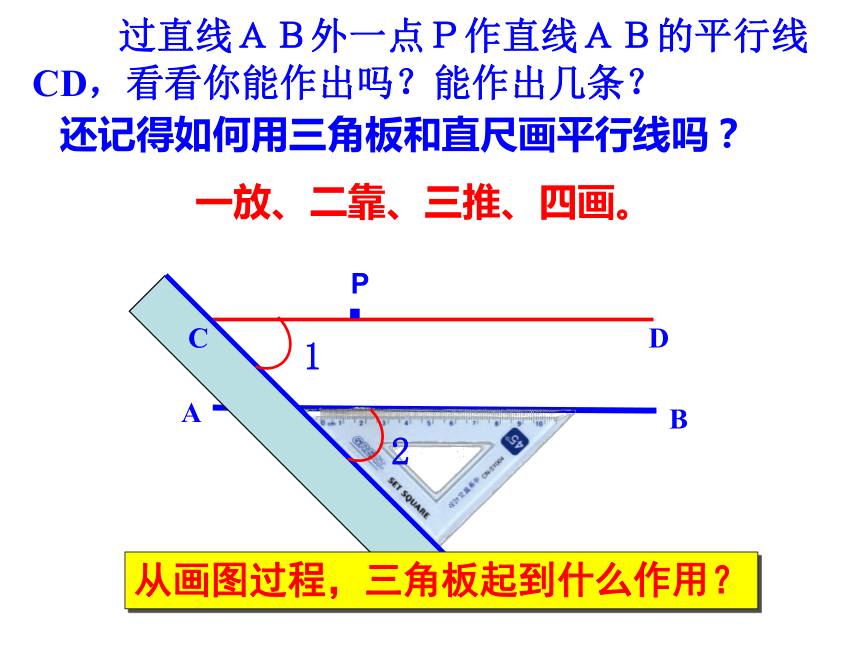
除应用以上两种方法以外,是否还有其它方法呢? 如果两条直线同平行于一条直线,那么两条直线平行。平行公理的推论(平行线的传递性): 过直线AB外一点P作直线AB的平行线CD,看看你能作出吗?能作出几条?· A B P还记得如何用三角板和直尺画平行线吗?一放、二靠、三推、四画。从画图过程,三角板起到什么作用? C D12 两条直线被第三条直线所截,
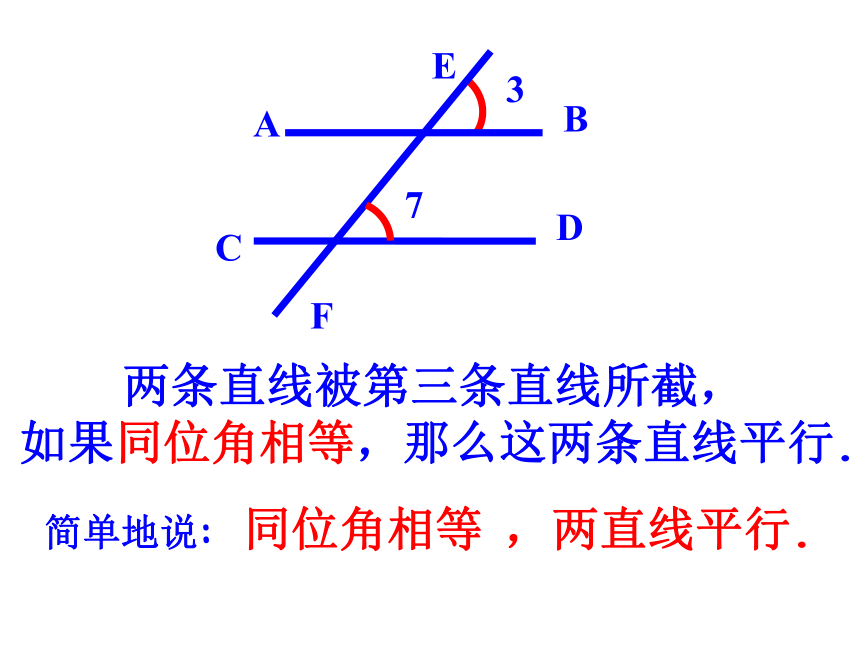
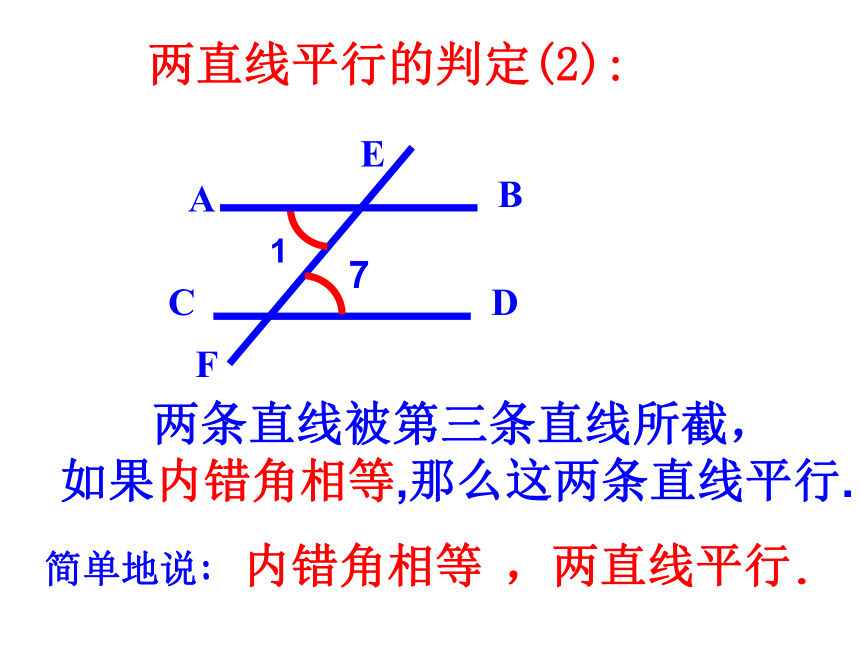
如果同位角相等,那么这两条直线平行.
简单地说: 同位角相等 ,两直线平行.
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。
简单地说:
同位角相等,两直线平行。 ∵ ∠1=∠2(已知)∴ a∥b(同位角相等,两直线平行)推论书写:条件: 1、同位角. 2、 相等.
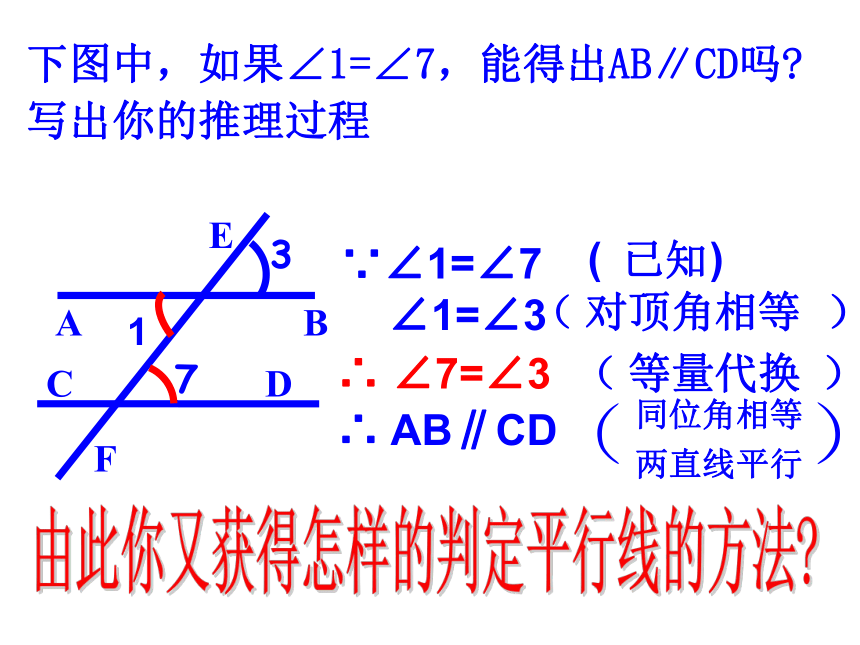
结论: 两条构成同位角的被截的直线平行.两直线平行的判定(1): 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?思考:下图中,如果∠1=∠7,能得出AB∥CD吗?
写出你的推理过程∵∠1=∠7
∠1=∠3
∴ ∠7=∠3∴ AB∥CDB1ACDF37E由此你又获得怎样的判定平行线的方法?
( ) 已知 ( ) 对顶角相等( ) 等量代换 ( )
同位角相等
两直线平行 两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行.C两直线平行的判定(2):简单地说: 内错角相等 ,两直线平行.
内错角相等,两直线平行。条件: 1、 内错角. 2、 相等.
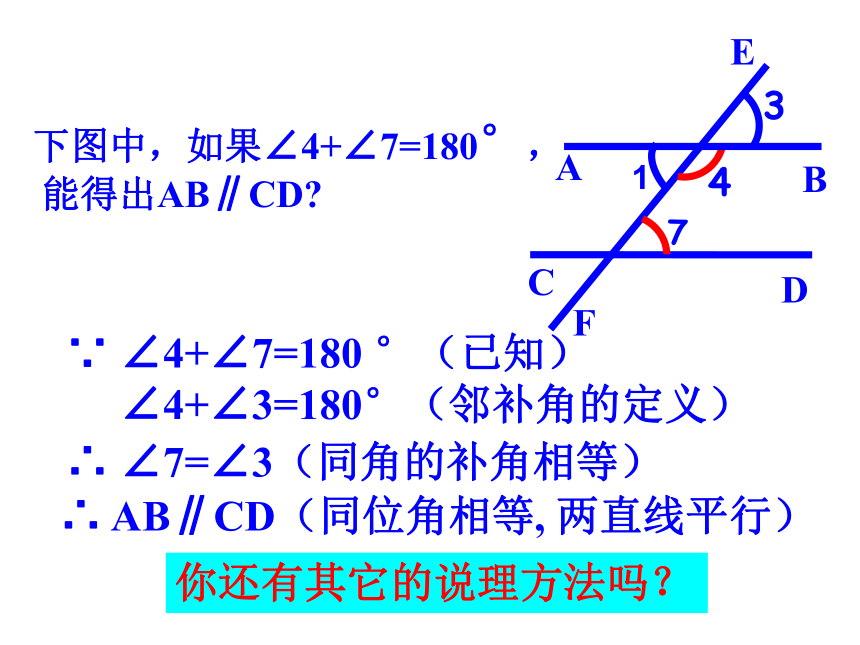
结论: 两条构成内错角的被截的直线平行.两直线平行的判定(2):推论书写: ∵ ∠1=∠2(已知)∴ a∥b(内错角相等,两直线平行)下图中,如果∠4+∠7=180°,
能得出AB∥CD?∵ ∠4+∠7=180 °(已知)
∠4+∠3=180°(邻补角的定义)
∴ ∠7=∠3(同角的补角相等)∴ AB∥CD(同位角相等, 两直线平行)你还有其它的说理方法吗?方法2∵ ∠4+∠7=180 °(已知)
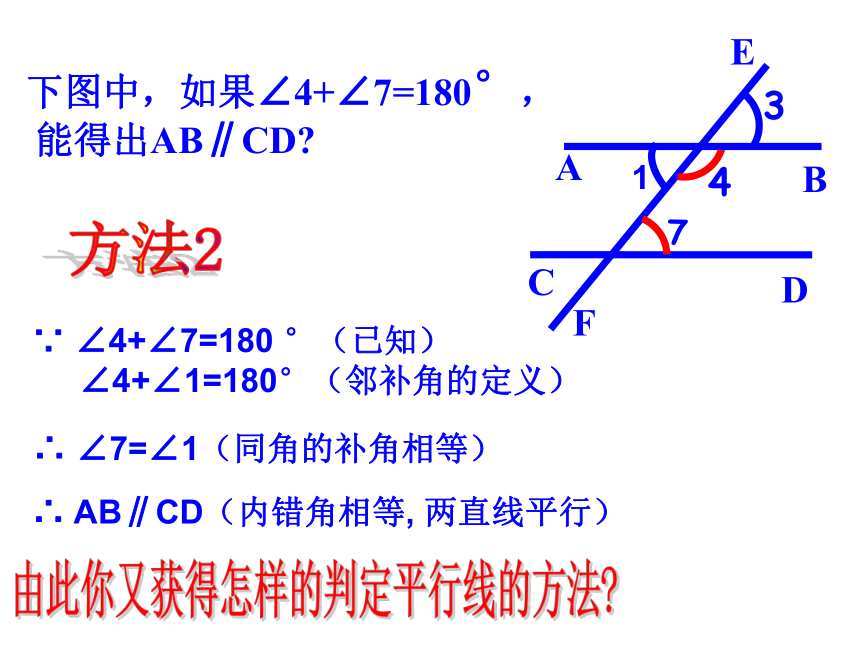
∠4+∠1=180°(邻补角的定义)∴ ∠7=∠1(同角的补角相等)∴ AB∥CD(内错角相等, 两直线平行)下图中,如果∠4+∠7=180°,
能得出AB∥CD?由此你又获得怎样的判定平行线的方法? 两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行.简单地说:同旁内角互补,两直线平行.两直线平行的判定(3):同旁内角互补,两直线平行。条件: 1、同旁内角. 2、 互补.
结论: 两条构成同旁内角的被截的直线平行.两直线平行的判定(3): ∵ ∠1+∠2=180°(已知)∴ a∥b(同旁内角互补,两直线平行)推论书写:同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结例1① ∵ ∠2 = ∠ 6(已知)
∴ ___∥___( )② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )③∵ ∠4 +___=180o(已知)
∴ ___∥___( )ABCDABCD∠5ABCDAC14235867BD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行平行线的判定FE① ∵ ∠1 =_____(已知)
∴ AB∥CE( )② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )ABCE∠2④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )∠3∠313542CFEADB内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行例2平行线的判定如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?例3平行线的判定还有其它解法吗?如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?AC1423BD5例3平行线的判定FE75o105o已知∠3=45°,∠1与∠2互余,试说明 ? 解:由于∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)123ABCD变式AB//CD45°∴∠ 2=∠3∴ AB∥CD(内错角相等,两直线平行)还有其它解法吗?∴∠ 1=∠3∴ AB∥CD(同位角相等,两直线平行)3.两条直线垂直于同一条直线,这两条直线
平行吗?为什么?答:垂直于同一条直线的两条直线平行.abc12探究∵b⊥a ,c ⊥a (已知)∴b∥c(同位角相等,两直线平行)∴∠1= ∠2 = 90° (垂直的定义)解法1:
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:答:垂直于同一条直线的两条直线平行.∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12解法3:答:垂直于同一条直线的两条直线平行.结论如果两条直线都垂直于同一条直线,
那么这两条直线平行。bc12a垂直于同一条直线的两条直线平行.简说为: 有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?试一试12方案1:40° 40° 40°1240°方案2:140° 40°方案3:1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行。
判定两条直线是否平行的方法有:当堂检测如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。能力拓展如图:若∠AOD= ∠A+ ∠D,试判断AC与BD是否平行?
除应用以上两种方法以外,是否还有其它方法呢? 如果两条直线同平行于一条直线,那么两条直线平行。平行公理的推论(平行线的传递性): 过直线AB外一点P作直线AB的平行线CD,看看你能作出吗?能作出几条?· A B P还记得如何用三角板和直尺画平行线吗?一放、二靠、三推、四画。从画图过程,三角板起到什么作用? C D12 两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行.
简单地说: 同位角相等 ,两直线平行.
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。
简单地说:
同位角相等,两直线平行。 ∵ ∠1=∠2(已知)∴ a∥b(同位角相等,两直线平行)推论书写:条件: 1、同位角. 2、 相等.
结论: 两条构成同位角的被截的直线平行.两直线平行的判定(1): 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?思考:下图中,如果∠1=∠7,能得出AB∥CD吗?
写出你的推理过程∵∠1=∠7
∠1=∠3
∴ ∠7=∠3∴ AB∥CDB1ACDF37E由此你又获得怎样的判定平行线的方法?
( ) 已知 ( ) 对顶角相等( ) 等量代换 ( )
同位角相等
两直线平行 两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行.C两直线平行的判定(2):简单地说: 内错角相等 ,两直线平行.
内错角相等,两直线平行。条件: 1、 内错角. 2、 相等.
结论: 两条构成内错角的被截的直线平行.两直线平行的判定(2):推论书写: ∵ ∠1=∠2(已知)∴ a∥b(内错角相等,两直线平行)下图中,如果∠4+∠7=180°,
能得出AB∥CD?∵ ∠4+∠7=180 °(已知)
∠4+∠3=180°(邻补角的定义)
∴ ∠7=∠3(同角的补角相等)∴ AB∥CD(同位角相等, 两直线平行)你还有其它的说理方法吗?方法2∵ ∠4+∠7=180 °(已知)
∠4+∠1=180°(邻补角的定义)∴ ∠7=∠1(同角的补角相等)∴ AB∥CD(内错角相等, 两直线平行)下图中,如果∠4+∠7=180°,
能得出AB∥CD?由此你又获得怎样的判定平行线的方法? 两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行.简单地说:同旁内角互补,两直线平行.两直线平行的判定(3):同旁内角互补,两直线平行。条件: 1、同旁内角. 2、 互补.
结论: 两条构成同旁内角的被截的直线平行.两直线平行的判定(3): ∵ ∠1+∠2=180°(已知)∴ a∥b(同旁内角互补,两直线平行)推论书写:同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结例1① ∵ ∠2 = ∠ 6(已知)
∴ ___∥___( )② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )③∵ ∠4 +___=180o(已知)
∴ ___∥___( )ABCDABCD∠5ABCDAC14235867BD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行平行线的判定FE① ∵ ∠1 =_____(已知)
∴ AB∥CE( )② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )ABCE∠2④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )∠3∠313542CFEADB内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行例2平行线的判定如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?例3平行线的判定还有其它解法吗?如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?AC1423BD5例3平行线的判定FE75o105o已知∠3=45°,∠1与∠2互余,试说明 ? 解:由于∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)123ABCD变式AB//CD45°∴∠ 2=∠3∴ AB∥CD(内错角相等,两直线平行)还有其它解法吗?∴∠ 1=∠3∴ AB∥CD(同位角相等,两直线平行)3.两条直线垂直于同一条直线,这两条直线
平行吗?为什么?答:垂直于同一条直线的两条直线平行.abc12探究∵b⊥a ,c ⊥a (已知)∴b∥c(同位角相等,两直线平行)∴∠1= ∠2 = 90° (垂直的定义)解法1:
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:答:垂直于同一条直线的两条直线平行.∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12解法3:答:垂直于同一条直线的两条直线平行.结论如果两条直线都垂直于同一条直线,
那么这两条直线平行。bc12a垂直于同一条直线的两条直线平行.简说为: 有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?试一试12方案1:40° 40° 40°1240°方案2:140° 40°方案3:1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行。
判定两条直线是否平行的方法有:当堂检测如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。能力拓展如图:若∠AOD= ∠A+ ∠D,试判断AC与BD是否平行?
