2018年高中数学第一章导数及其应用1.4.1曲边梯形的面积与定积分课件 新人教B版选修2_2(27张)
文档属性
| 名称 | 2018年高中数学第一章导数及其应用1.4.1曲边梯形的面积与定积分课件 新人教B版选修2_2(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 634.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 21:00:48 | ||
图片预览


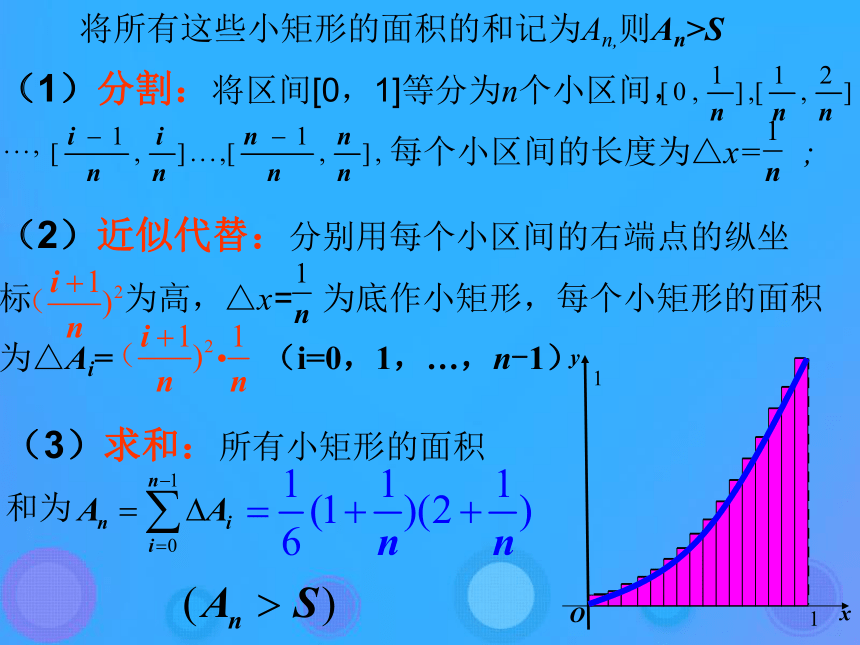


文档简介
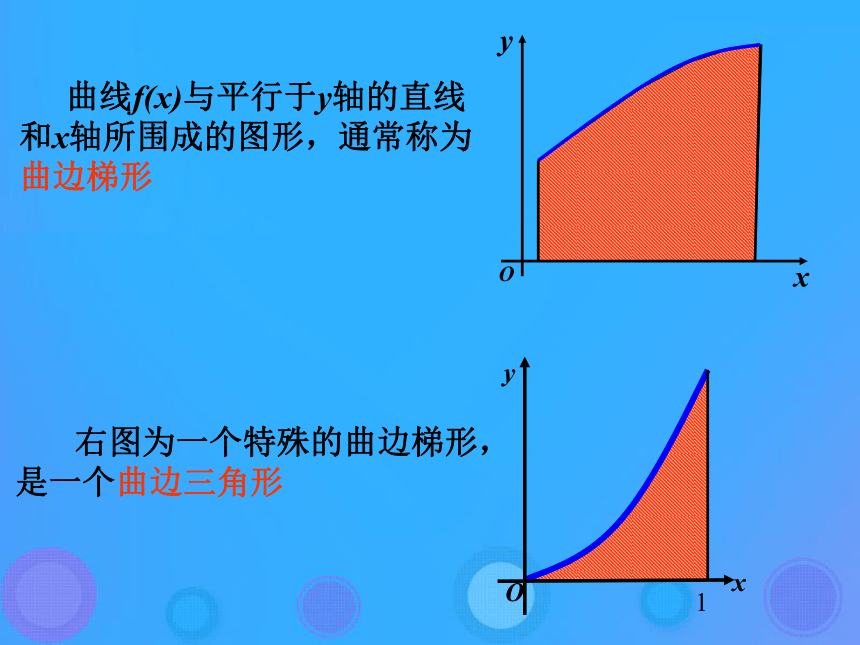
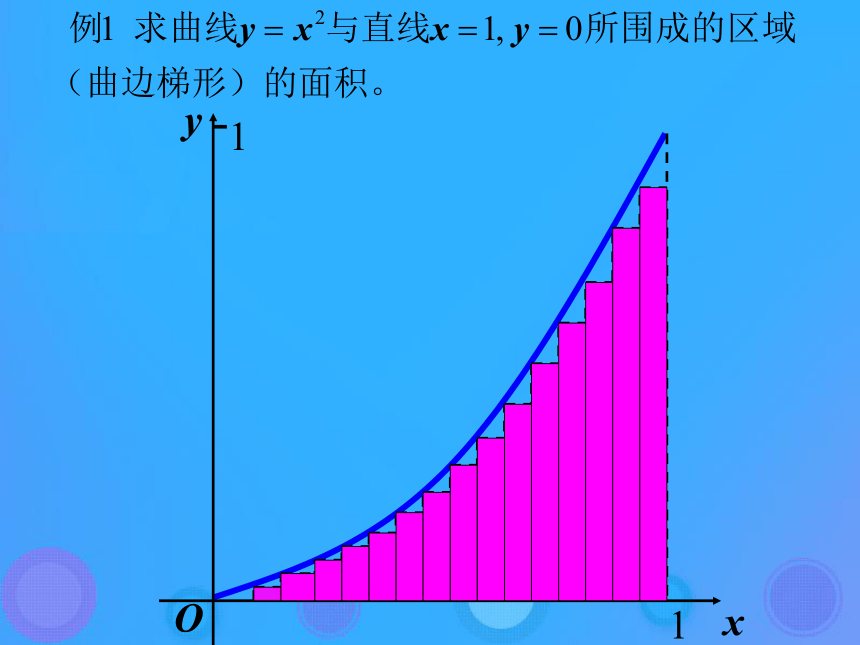
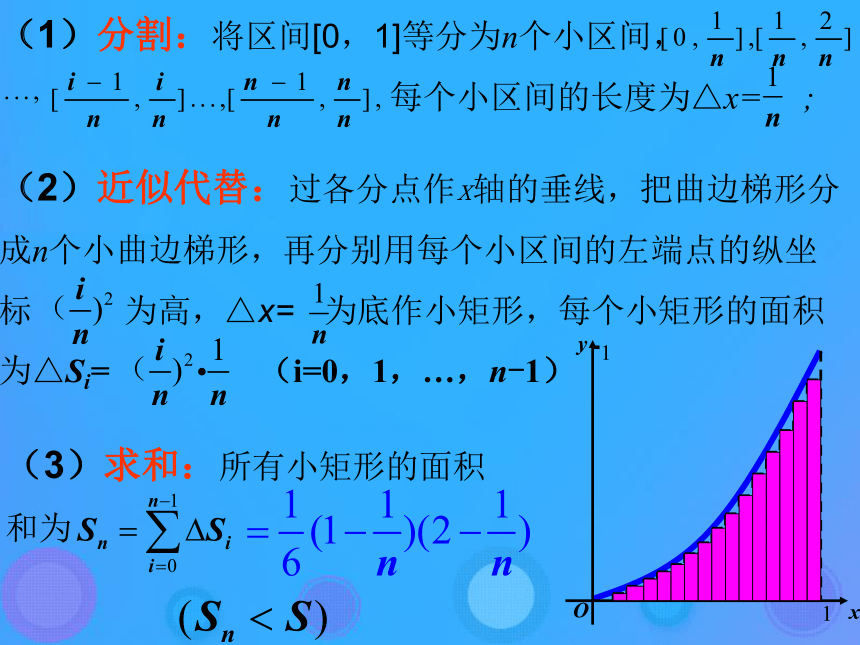
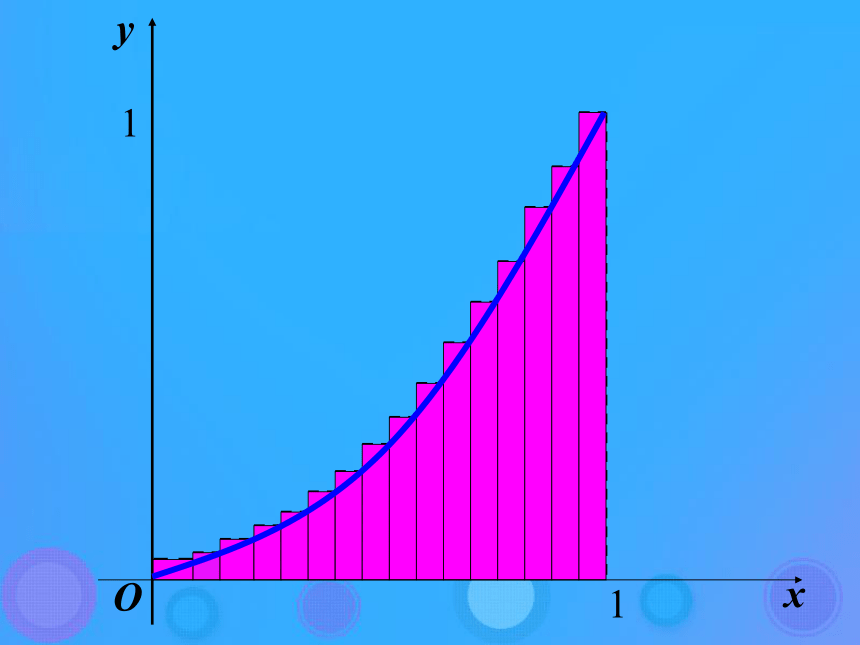
课件27张PPT。1.4.1 曲边梯形面积与定积分 曲线f(x)与平行于y轴的直线和x轴所围成的图形,通常称为曲边梯形 右图为一个特殊的曲边梯形,是一个曲边三角形(4)取极限:所以曲边三角形的面积为 “分割”的目的在于更精确地“以直代曲”,以“矩形”代替“曲边梯形”,随着分割的等份数的增多,这种“代替”就越精确,当n愈大时,划分就越细,所有的小矩形的面积的和就愈接近曲边三角形的面积。 在”近似代替“中,是否可以取每个区间的右端点的 纵坐标为小矩形的高,并且利用所有这些小矩形的面积的和去逼近曲边三角形的面积呢?思考:将所有这些小矩形的面积的和记为An,则An>S(4)取极限:所以曲边三角形的面积为 事实上,在”近似代替“中,可以取每个区间的左端点或右端点或区间上的任一点的纵坐标的绝对值为小矩形的高,没有统一的要求,只是 为了计算方便,通常取一些特殊点,并且利用所有这些小矩形的面积的和去逼近曲边梯形的面积。求曲边梯形的面积的步骤:(1)分割(2)近似代替(3)求和(4)取极限利用曲边梯形的面积的求法解决变力做功问题(3)求和:
(4)取极限:所以弹簧从平衡位置拉长b所做的功为 以上两个问题解决问题的方法和步骤是完全相同的,都归结为求一个函数在某一闭区间上的和式的极限问题:曲边三角形或曲边梯形的面积克服弹簧拉力的变力所做的功 牛顿等数学家得到解决这类问题的一般方法:
求函数的定积分 曲边梯形的面积S等于其曲边所对应的函数 y=f(x)在区
间[a,b]上的定积分,即例2中克服弹簧拉力的变力所做的功可以写为例1的结果可以写为①分割②近似代替③求和④取极限表示曲边梯形的面积表示x轴上方和下方的面积的代数和注:运算性质1: 运算性质2: 运算性质3: 运算性质4: 定积分的运算性质:图中阴影部分面积用定积分该如何表示?思考: 2.用定积分求直线y=x,x=1,x=2,y=0所围成的梯形的面积。几种典型的曲边梯形面积的求法:曲边梯形的面积为:曲边梯形的面积为:阴影部分的面积为:动动脑
(4)取极限:所以弹簧从平衡位置拉长b所做的功为 以上两个问题解决问题的方法和步骤是完全相同的,都归结为求一个函数在某一闭区间上的和式的极限问题:曲边三角形或曲边梯形的面积克服弹簧拉力的变力所做的功 牛顿等数学家得到解决这类问题的一般方法:
求函数的定积分 曲边梯形的面积S等于其曲边所对应的函数 y=f(x)在区
间[a,b]上的定积分,即例2中克服弹簧拉力的变力所做的功可以写为例1的结果可以写为①分割②近似代替③求和④取极限表示曲边梯形的面积表示x轴上方和下方的面积的代数和注:运算性质1: 运算性质2: 运算性质3: 运算性质4: 定积分的运算性质:图中阴影部分面积用定积分该如何表示?思考: 2.用定积分求直线y=x,x=1,x=2,y=0所围成的梯形的面积。几种典型的曲边梯形面积的求法:曲边梯形的面积为:曲边梯形的面积为:阴影部分的面积为:动动脑
