第9章 多边形 单元测试卷(含答案)
文档属性
| 名称 | 第9章 多边形 单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 601.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 17:07:40 | ||
图片预览


文档简介
第9章 多边形
一、选择题(每题3分,共30分)
1.[2017·黔东南]如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
A.120° B.90° C.100° D.30°
2.[2017·乌鲁木齐]如果正n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
A.4 B.5 C.6 D.7
3.如图,张明同学设计了四种正多边形的瓷砖图案,在这四种瓷砖图案中,不能铺满地面的是( )
A B C D
4.在下列条件中:
①∠A+∠B=∠C;②∠A∶∠B∶∠C=1∶2∶3;
③∠A=∠B=∠C;④∠A=∠B=2∠C;⑤∠A=∠B=∠C.
能确定△ABC为直角三角形的条件有( )
A.5个 B.4个 C.3个 D.2个
5.已知三角形的三边长分别为3、x、14.若x为正整数,则这样的三角形共有( )
A.2个 B.3个 C.5个 D.7个
6.如图,在△ABC中,点D在边BA的延长线上,∠ABC的平分线和∠DAC的平分线相交于点M.若∠BAC=80°,∠C=60°,则∠M的大小为( )
A.20° B.25° C.30° D.35°
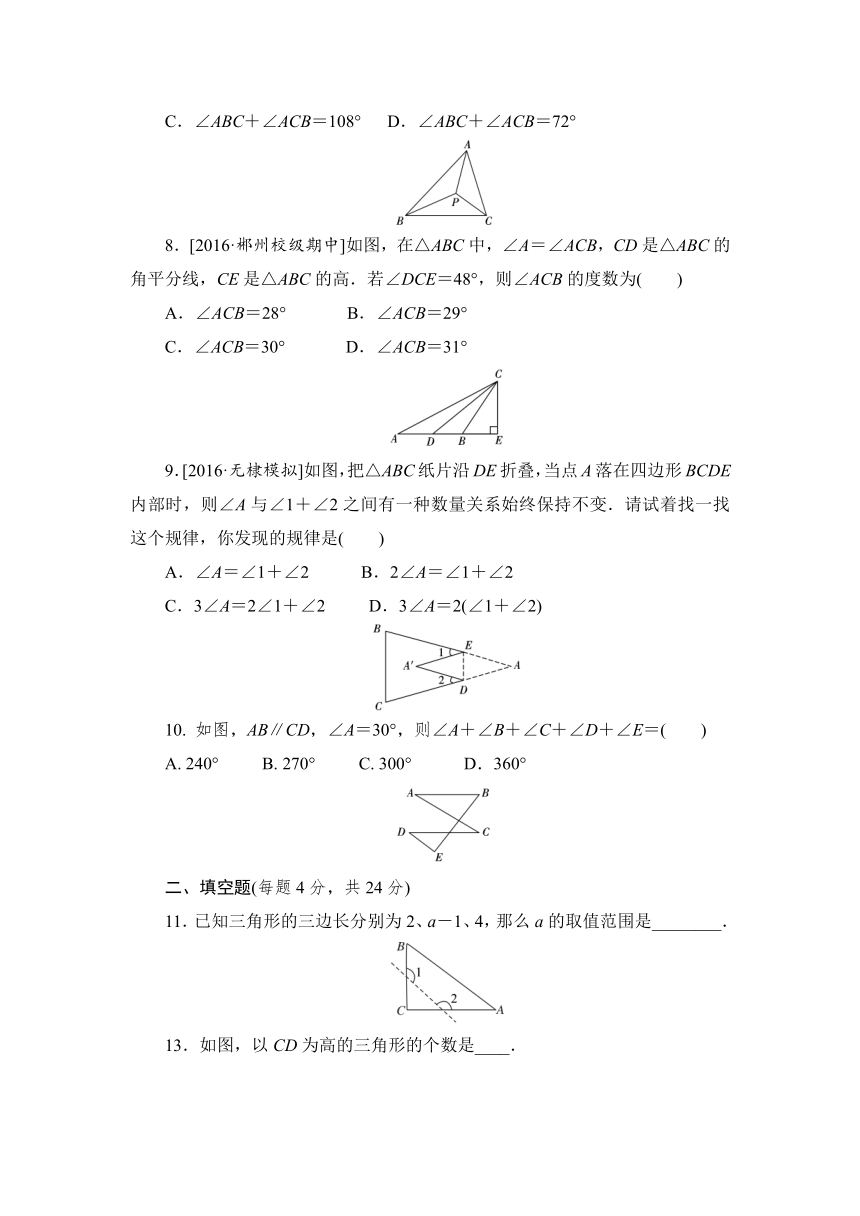
7.如图,点P是△ABC三条角平分线的交点.若∠BPC=108°,则下列结论中正确的是( )
A.∠BAC=54° B.∠BAC=36°
C.∠ABC+∠ACB=108° D.∠ABC+∠ACB=72°
8.[2016·郴州校级期中]如图,在△ABC中,∠A=∠ACB,CD是△ABC的角平分线,CE是△ABC的高.若∠DCE=48°,则∠ACB的度数为( )
A.∠ACB=28° B.∠ACB=29°
C.∠ACB=30° D.∠ACB=31°
9.[2016·无棣模拟]如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
10. 如图,AB∥CD,∠A=30°,则∠A+∠B+∠C+∠D+∠E=( )
A. 240° B. 270° C. 300° D.360°
二、填空题(每题4分,共24分)
11.已知三角形的三边长分别为2、a-1、4,那么a的取值范围是________.
13.如图,以CD为高的三角形的个数是____.
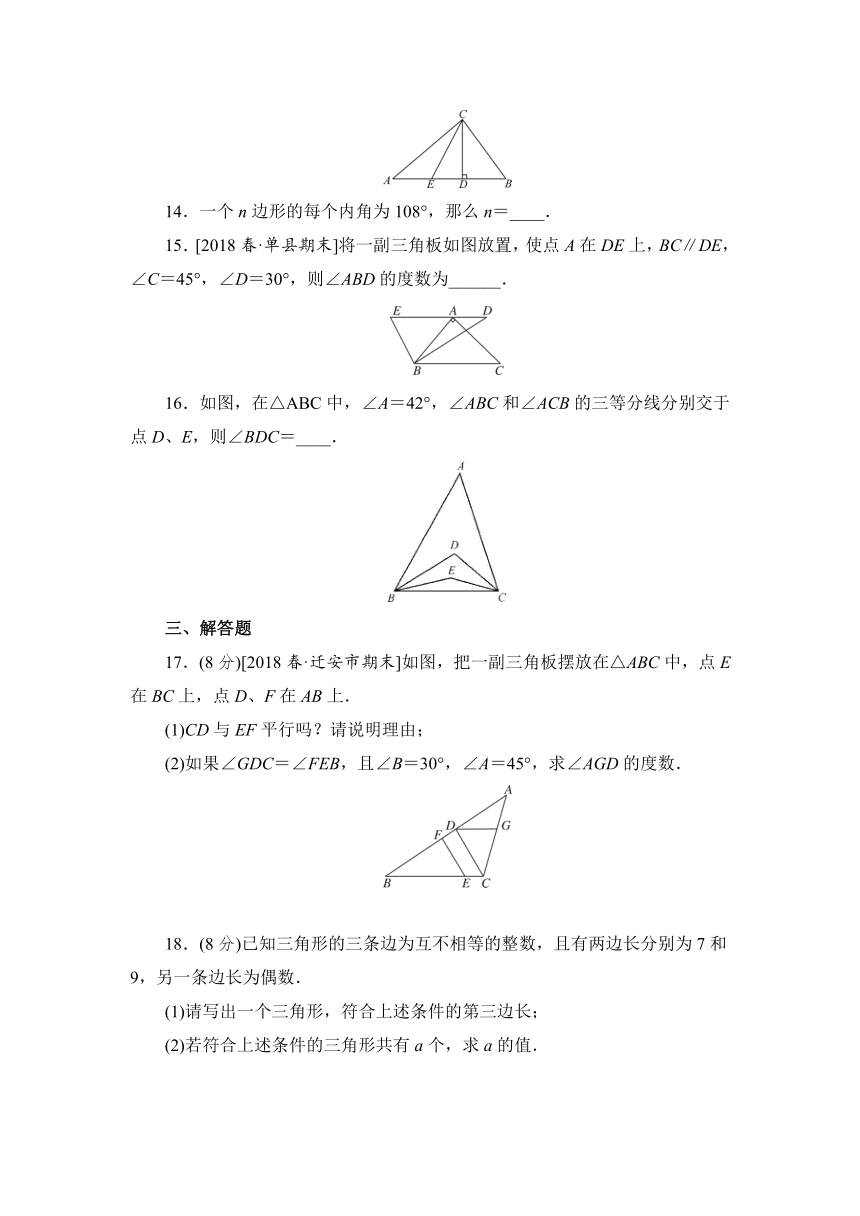
14.一个n边形的每个内角为108°,那么n=____.
15.[2018春·单县期末]将一副三角板如图放置,使点A在DE上,BC∥DE,∠C=45°,∠D=30°,则∠ABD的度数为______.
16.如图,在△ABC中,∠A=42°,∠ABC和∠ACB的三等分线分别交于点D、E,则∠BDC=____.
三、解答题
17.(8分)[2018春·迁安市期末]如图,把一副三角板摆放在△ABC中,点E在BC上,点D、F在AB上.
(1)CD与EF平行吗?请说明理由;
(2)如果∠GDC=∠FEB,且∠B=30°,∠A=45°,求∠AGD的度数.
18.(8分)已知三角形的三条边为互不相等的整数,且有两边长分别为7和9,另一条边长为偶数.
(1)请写出一个三角形,符合上述条件的第三边长;
(2)若符合上述条件的三角形共有a个,求a的值.
19.(8分)如图,在锐角△ABC中,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数;
(2)若BE,CD平分∠ABC和∠ACB,求∠BHC的度数.
20.(8分)[2018春·兴化市期末]如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
21.(10分)[2018春·灵石县期末]如图,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,CF∥AD.
(1)若∠B=30°,∠ACB=70°,求∠CFE的度数;
(2)若(1)中的∠B=α,∠ACB=β,求∠CFE的度数.(用α、β表示)
22.(12分)如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
(1)试探求∠F与∠B、∠D之间的关系;
(2)若∠B∶∠D∶∠F=2∶4∶x,求x的值.
23.(12分)(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.在△ABC中,∠A=30°,求∠ABC+∠ACB、∠XBC+∠XCB的值.
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
图1 图2
参考答案
1. C
2. C
【解析】 设该正多边形的外角为x°,则相邻的内角为2x°.根据“外角与相邻的内角互补”,得x+2x=180,解得x=60.根据多边形的外角和是360°,有n==6.
3. C
【解析】 用一种正多边形瓷砖铺满地面的条件是:正多边形的一个内角是360°的约数.由此可判断正五边形瓷砖不能铺满地面.
4. B
5. C
【解析】 由题可得11<x<17.∵x为正整数,∴x的可能取值是12、13、14、15、16,共5个,故这样的三角形共有5个.
6. C
【解析】 ∵∠BAC=80°,∠C=60°,∴∠ABC=40°.∵∠ABC的平分线和∠DAC的平分线相交于点M,∴∠ABM=20°,∠CAM=×(180°-80°)=50°,∴∠M=180°-20°-50°-80°=30°.
7. B
8. A
【解析】 设∠A为2x,则∠ACB=2x,∠ACD=x,∴∠CBE=∠A+∠ACB=4x,∠CDB=∠A+∠ACD=3x,∴∠CDB=3∠DCB.∵∠DCE=48°,∴∠CDB=90°-48°=42°,∴∠DCB=14°,∴∠ACB=28°.
9. B
【解析】2∠A=∠1+∠2.理由:∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,则2∠A+180°-∠2+180°-∠1=360°,∴2∠A=∠1+∠2.
10. A
【解析】 如答图,∵AB∥CD,∠A=30°,∴∠C=∠A=30°,∠B=∠1.又∵∠1+∠D+∠E=180°,∴∠A+∠B+∠C+∠D+∠E=30°+30°+180°=240°.
11. 3<a<7
【解析】 根据三角形的三边关系,有4-2<a-1<4+2,解得3<a<7.
12. 270°
13. 6
【解析】 CD分别是△ABC,△CEB,△CDB,△ADC,△CED,△AEC的高,共6个三角形.
14. 5
【解析】 根据多边形的内角和公式可知(n-2)×180°=108°n,解得n=5.
15. 15°
【解析】 ∵Rt△ABC中,∠C=45°,∴∠ABC=45°.∵BC∥DE,∠D=30°,∴∠DBC=30°,∴∠ABD=45°-30°=15°.
16. 88°
【解析】 ∵∠A=42°,∴∠ABC+∠ACB=180°-42°=138°,∴∠DBC+∠DCB=×138°=92°,∴∠BDC=180°-92°=88°.
17. 解:(1)CD∥EF.
理由:∵∠CDF=∠EFB=90°,
∴CD∥EF.
(2)∵∠B=30°,∠A=45°,
∴∠FEB=60°,∠ACD=45°.
∵∠GDC=∠FEB,
∴∠GDC=60°.
∵∠AGD=∠GDC+∠ACD,
∴∠AGD=60°+45°=105°.
18.解:两边长分别为9和7,设第三边是n,
则9-7<n<7+9,即2<n<16.
(1)第三边长是4(答案不唯一).
(2)∵2<n<16,且n为偶数,
∴n的值为4、6、8、10、12、14,共6个,∴a=6.
19. 解:(1)∵BE⊥AC,∠ACB=70°,
∴∠EBC=90°-70°=20°.
∵CD⊥AB,∠ABC=40°,
∴∠DCB=90°-40°=50°,
∴∠BHC=180°-20°-50°=110°.
(2)∵BE平分∠ABC,∠ABC=40°,
∴∠EBC=20°.
∵DC平分∠ACB,∠ACB=70°,
∴∠DCB=35°,
∴∠BHC=180°-20°-35°=125°.
20. 解:(1)∵∠A=50°,∠C=30°,
∴∠BDO=∠A+∠C=80°.
∵∠BOD=70°,
∴∠B=180°-∠BDO-∠BOD=30°.
(2)∠BOC=∠A+∠B+∠C.
证明:∵∠BEC=∠A+∠B,
∴∠BOC=∠BEC+∠C=∠A+∠B+∠C.
21. 解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°-∠B-∠ACB=80°.
∵AD平分∠BAC,
∴∠BAD=40°.
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=60°,
∴∠DAE=∠BAE-∠BAD=60°-40°=20°.
∵CF∥AD,
∴∠CFE=∠DAE=20°,
(2)∵∠BAE=90°-∠B,∠BAD=∠BAC=(180°-∠B-∠BCA),
∴∠CFE=∠DAE=∠BAE-∠BAD=90°-∠B-(180°-∠B-∠BCA)=(∠BCA-∠B)=β-α.
22.
解:(1)如答图,∵CF为∠BCD的平分线,
EF为∠BED的平分线,
∴∠1=∠2,∠3=∠4.
∵∠D+∠1=∠F+∠3,
∠B+∠4=∠F+∠2,
∴∠B+∠D+∠1+∠4=2∠F+∠3+∠2,
∴∠F=(∠B+∠D).
(2)当∠B∶∠D∶∠F=2∶4∶x时,
设∠B=2a(a≠0),则∠D=4a,∠F=ax.
∵2∠F=∠B+∠D,∴2ax=2a+4a,
∴2x=2+4,∴x=3.
23.解: (1)∵∠A=30°,
∴∠ABC+∠ACB=150°.
∵∠X=90°,
∴∠XBC+∠XCB=90°.
(2)不变化.
∵∠A=30°,
∴∠ABC+∠ACB=150°.
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)=
(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
一、选择题(每题3分,共30分)
1.[2017·黔东南]如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
A.120° B.90° C.100° D.30°
2.[2017·乌鲁木齐]如果正n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
A.4 B.5 C.6 D.7
3.如图,张明同学设计了四种正多边形的瓷砖图案,在这四种瓷砖图案中,不能铺满地面的是( )
A B C D
4.在下列条件中:
①∠A+∠B=∠C;②∠A∶∠B∶∠C=1∶2∶3;
③∠A=∠B=∠C;④∠A=∠B=2∠C;⑤∠A=∠B=∠C.
能确定△ABC为直角三角形的条件有( )
A.5个 B.4个 C.3个 D.2个
5.已知三角形的三边长分别为3、x、14.若x为正整数,则这样的三角形共有( )
A.2个 B.3个 C.5个 D.7个
6.如图,在△ABC中,点D在边BA的延长线上,∠ABC的平分线和∠DAC的平分线相交于点M.若∠BAC=80°,∠C=60°,则∠M的大小为( )
A.20° B.25° C.30° D.35°
7.如图,点P是△ABC三条角平分线的交点.若∠BPC=108°,则下列结论中正确的是( )
A.∠BAC=54° B.∠BAC=36°
C.∠ABC+∠ACB=108° D.∠ABC+∠ACB=72°
8.[2016·郴州校级期中]如图,在△ABC中,∠A=∠ACB,CD是△ABC的角平分线,CE是△ABC的高.若∠DCE=48°,则∠ACB的度数为( )
A.∠ACB=28° B.∠ACB=29°
C.∠ACB=30° D.∠ACB=31°
9.[2016·无棣模拟]如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
10. 如图,AB∥CD,∠A=30°,则∠A+∠B+∠C+∠D+∠E=( )
A. 240° B. 270° C. 300° D.360°
二、填空题(每题4分,共24分)
11.已知三角形的三边长分别为2、a-1、4,那么a的取值范围是________.
13.如图,以CD为高的三角形的个数是____.
14.一个n边形的每个内角为108°,那么n=____.
15.[2018春·单县期末]将一副三角板如图放置,使点A在DE上,BC∥DE,∠C=45°,∠D=30°,则∠ABD的度数为______.
16.如图,在△ABC中,∠A=42°,∠ABC和∠ACB的三等分线分别交于点D、E,则∠BDC=____.
三、解答题
17.(8分)[2018春·迁安市期末]如图,把一副三角板摆放在△ABC中,点E在BC上,点D、F在AB上.
(1)CD与EF平行吗?请说明理由;
(2)如果∠GDC=∠FEB,且∠B=30°,∠A=45°,求∠AGD的度数.
18.(8分)已知三角形的三条边为互不相等的整数,且有两边长分别为7和9,另一条边长为偶数.
(1)请写出一个三角形,符合上述条件的第三边长;
(2)若符合上述条件的三角形共有a个,求a的值.
19.(8分)如图,在锐角△ABC中,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数;
(2)若BE,CD平分∠ABC和∠ACB,求∠BHC的度数.
20.(8分)[2018春·兴化市期末]如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
21.(10分)[2018春·灵石县期末]如图,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,CF∥AD.
(1)若∠B=30°,∠ACB=70°,求∠CFE的度数;
(2)若(1)中的∠B=α,∠ACB=β,求∠CFE的度数.(用α、β表示)
22.(12分)如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
(1)试探求∠F与∠B、∠D之间的关系;
(2)若∠B∶∠D∶∠F=2∶4∶x,求x的值.
23.(12分)(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.在△ABC中,∠A=30°,求∠ABC+∠ACB、∠XBC+∠XCB的值.
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
图1 图2
参考答案
1. C
2. C
【解析】 设该正多边形的外角为x°,则相邻的内角为2x°.根据“外角与相邻的内角互补”,得x+2x=180,解得x=60.根据多边形的外角和是360°,有n==6.
3. C
【解析】 用一种正多边形瓷砖铺满地面的条件是:正多边形的一个内角是360°的约数.由此可判断正五边形瓷砖不能铺满地面.
4. B
5. C
【解析】 由题可得11<x<17.∵x为正整数,∴x的可能取值是12、13、14、15、16,共5个,故这样的三角形共有5个.
6. C
【解析】 ∵∠BAC=80°,∠C=60°,∴∠ABC=40°.∵∠ABC的平分线和∠DAC的平分线相交于点M,∴∠ABM=20°,∠CAM=×(180°-80°)=50°,∴∠M=180°-20°-50°-80°=30°.
7. B
8. A
【解析】 设∠A为2x,则∠ACB=2x,∠ACD=x,∴∠CBE=∠A+∠ACB=4x,∠CDB=∠A+∠ACD=3x,∴∠CDB=3∠DCB.∵∠DCE=48°,∴∠CDB=90°-48°=42°,∴∠DCB=14°,∴∠ACB=28°.
9. B
【解析】2∠A=∠1+∠2.理由:∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,则2∠A+180°-∠2+180°-∠1=360°,∴2∠A=∠1+∠2.
10. A
【解析】 如答图,∵AB∥CD,∠A=30°,∴∠C=∠A=30°,∠B=∠1.又∵∠1+∠D+∠E=180°,∴∠A+∠B+∠C+∠D+∠E=30°+30°+180°=240°.
11. 3<a<7
【解析】 根据三角形的三边关系,有4-2<a-1<4+2,解得3<a<7.
12. 270°
13. 6
【解析】 CD分别是△ABC,△CEB,△CDB,△ADC,△CED,△AEC的高,共6个三角形.
14. 5
【解析】 根据多边形的内角和公式可知(n-2)×180°=108°n,解得n=5.
15. 15°
【解析】 ∵Rt△ABC中,∠C=45°,∴∠ABC=45°.∵BC∥DE,∠D=30°,∴∠DBC=30°,∴∠ABD=45°-30°=15°.
16. 88°
【解析】 ∵∠A=42°,∴∠ABC+∠ACB=180°-42°=138°,∴∠DBC+∠DCB=×138°=92°,∴∠BDC=180°-92°=88°.
17. 解:(1)CD∥EF.
理由:∵∠CDF=∠EFB=90°,
∴CD∥EF.
(2)∵∠B=30°,∠A=45°,
∴∠FEB=60°,∠ACD=45°.
∵∠GDC=∠FEB,
∴∠GDC=60°.
∵∠AGD=∠GDC+∠ACD,
∴∠AGD=60°+45°=105°.
18.解:两边长分别为9和7,设第三边是n,
则9-7<n<7+9,即2<n<16.
(1)第三边长是4(答案不唯一).
(2)∵2<n<16,且n为偶数,
∴n的值为4、6、8、10、12、14,共6个,∴a=6.
19. 解:(1)∵BE⊥AC,∠ACB=70°,
∴∠EBC=90°-70°=20°.
∵CD⊥AB,∠ABC=40°,
∴∠DCB=90°-40°=50°,
∴∠BHC=180°-20°-50°=110°.
(2)∵BE平分∠ABC,∠ABC=40°,
∴∠EBC=20°.
∵DC平分∠ACB,∠ACB=70°,
∴∠DCB=35°,
∴∠BHC=180°-20°-35°=125°.
20. 解:(1)∵∠A=50°,∠C=30°,
∴∠BDO=∠A+∠C=80°.
∵∠BOD=70°,
∴∠B=180°-∠BDO-∠BOD=30°.
(2)∠BOC=∠A+∠B+∠C.
证明:∵∠BEC=∠A+∠B,
∴∠BOC=∠BEC+∠C=∠A+∠B+∠C.
21. 解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°-∠B-∠ACB=80°.
∵AD平分∠BAC,
∴∠BAD=40°.
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=60°,
∴∠DAE=∠BAE-∠BAD=60°-40°=20°.
∵CF∥AD,
∴∠CFE=∠DAE=20°,
(2)∵∠BAE=90°-∠B,∠BAD=∠BAC=(180°-∠B-∠BCA),
∴∠CFE=∠DAE=∠BAE-∠BAD=90°-∠B-(180°-∠B-∠BCA)=(∠BCA-∠B)=β-α.
22.
解:(1)如答图,∵CF为∠BCD的平分线,
EF为∠BED的平分线,
∴∠1=∠2,∠3=∠4.
∵∠D+∠1=∠F+∠3,
∠B+∠4=∠F+∠2,
∴∠B+∠D+∠1+∠4=2∠F+∠3+∠2,
∴∠F=(∠B+∠D).
(2)当∠B∶∠D∶∠F=2∶4∶x时,
设∠B=2a(a≠0),则∠D=4a,∠F=ax.
∵2∠F=∠B+∠D,∴2ax=2a+4a,
∴2x=2+4,∴x=3.
23.解: (1)∵∠A=30°,
∴∠ABC+∠ACB=150°.
∵∠X=90°,
∴∠XBC+∠XCB=90°.
(2)不变化.
∵∠A=30°,
∴∠ABC+∠ACB=150°.
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)=
(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
