2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.1.1指数与指数幂的运算第二课时指数幂及其运算性质课件新人教A版必修1(36张)
文档属性
| 名称 | 2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.1.1指数与指数幂的运算第二课时指数幂及其运算性质课件新人教A版必修1(36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 21:27:19 | ||
图片预览











文档简介
课件36张PPT。第二课时 指数幂及其运算性质目标导航新知探求课堂探究新知探求·素养养成想一想 根式与指数幂之间存在什么关系?
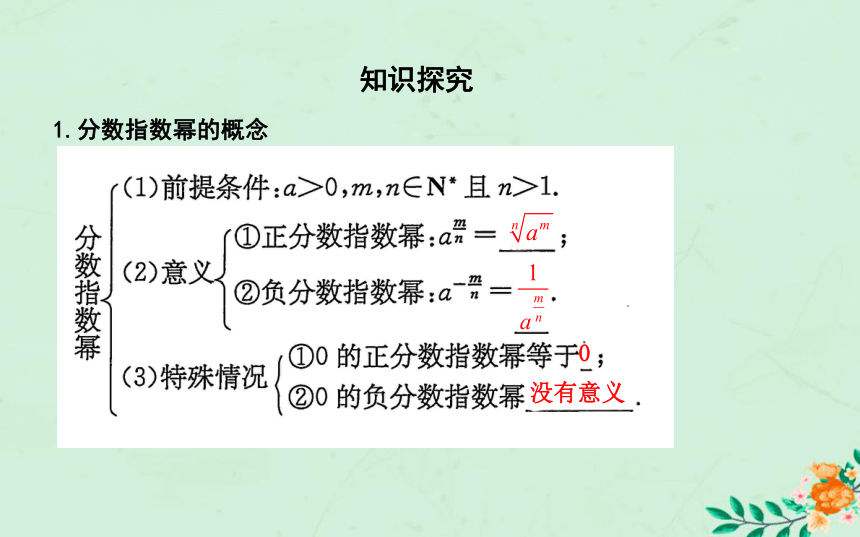
(无论被开方数的指数能否被根指数整除,根式都可以表示为分数指数幂的形式,即两者是等价的)知识探究1.分数指数幂的概念0没有意义2.有理数指数幂的运算性质
(1)aras= (a>0,r,s∈Q);
(2)(ar)s= (a>0,r,s∈Q);
(3)(ab)r= (a>0,b>0,r∈Q).ar+sarsarbr探究2:有理数指数幂的运算性质,对底数有何要求?
答案:底数大于0.
3.无理数指数幂
无理数指数幂aα(a>0,α是无理数)是一个确定的 .有理数指数幂的运算性质对于无理数指数幂同样适用.实数【拓展延伸】
化简与求值的方法与技巧
(1)在进行幂和根式的化简时,一般是先将根式化成幂的形式,并化小数指数幂为分数指数幂,即统一成分数指数幂的形式,再利用幂的运算性质进行化简、求值、计算.
(2)对于根式的计算结果,并不要求统一表示形式,一般用分数指数幂的形式来表示.若有特殊要求,则按要求给出结果,但结果中不能同时含有根式和分数指数幂,也不能既有分母又含有负指数,即结果必须化为最简的形式.
(3)在幂的四则混合运算中,运用乘法公式进行化简,能起到化繁为简的效果.
要注意的是:
①要把幂作为一个整体来看待;
②要注意幂指数间的倍数关系.(4)常用的变换方法有:
①把小数化为分数,把根式化为分数指数幂;
②若指数是负数,则对调底数的分子和分母并将负指数化为正指数;
③把分数指数幂、负指数幂看成一个整体,借助有理式中的乘法公式及因式分解进行变形.
(5)注意灵活运用分式化简的方法和技巧.例如,①把分子、分母分解因式,可约分的先约分;②利用分式的基本性质化繁分式为简分式,化异分母为同分母;③把适当的几个分式先化简,各个击破;④适当利用换元法.自我检测DAC答案:-3题型一根式与指数幂的互化课堂探究·素养提升名师导引:根式与分数指数幂的互化要求是什么?(①根指数?分数指数的分母;②被开方数(式)的指数?分数指数的分子) (1)根式与分数指数幂互化的关键是准确把握两种形式中相关数值的对应.①根指数?分数指数的分母;②被开方数(式)的指数?分数指数的分子.
(2)将含有多重根号的根式化为分数指数幂途径有两条:一是由里向外化为分数指数幂;二是由外向里化为分数指数幂.方法技巧题型二 利用指数幂的运算性质化简求值方法技巧 进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数为分数,化带分数为假分数进行运算,便于进行乘除、乘方、开方运算,以达到化繁为简的目的. 题型三 附加条件的幂的求值问题(2)将a+a-1=7两边平方,得a2+a-2+2=49,
所以a2+a-2=47.方法技巧 条件求值问题的基本步骤是先找条件和所求之间的关系,然后进行化简,最后代值运算,求值过程中要注意平方差公式、立方差公式以及一元二次方程中根与系数关系的灵活应用.题型四易错辨析——忽略 有意义出错谢谢观赏!
(无论被开方数的指数能否被根指数整除,根式都可以表示为分数指数幂的形式,即两者是等价的)知识探究1.分数指数幂的概念0没有意义2.有理数指数幂的运算性质
(1)aras= (a>0,r,s∈Q);
(2)(ar)s= (a>0,r,s∈Q);
(3)(ab)r= (a>0,b>0,r∈Q).ar+sarsarbr探究2:有理数指数幂的运算性质,对底数有何要求?
答案:底数大于0.
3.无理数指数幂
无理数指数幂aα(a>0,α是无理数)是一个确定的 .有理数指数幂的运算性质对于无理数指数幂同样适用.实数【拓展延伸】
化简与求值的方法与技巧
(1)在进行幂和根式的化简时,一般是先将根式化成幂的形式,并化小数指数幂为分数指数幂,即统一成分数指数幂的形式,再利用幂的运算性质进行化简、求值、计算.
(2)对于根式的计算结果,并不要求统一表示形式,一般用分数指数幂的形式来表示.若有特殊要求,则按要求给出结果,但结果中不能同时含有根式和分数指数幂,也不能既有分母又含有负指数,即结果必须化为最简的形式.
(3)在幂的四则混合运算中,运用乘法公式进行化简,能起到化繁为简的效果.
要注意的是:
①要把幂作为一个整体来看待;
②要注意幂指数间的倍数关系.(4)常用的变换方法有:
①把小数化为分数,把根式化为分数指数幂;
②若指数是负数,则对调底数的分子和分母并将负指数化为正指数;
③把分数指数幂、负指数幂看成一个整体,借助有理式中的乘法公式及因式分解进行变形.
(5)注意灵活运用分式化简的方法和技巧.例如,①把分子、分母分解因式,可约分的先约分;②利用分式的基本性质化繁分式为简分式,化异分母为同分母;③把适当的几个分式先化简,各个击破;④适当利用换元法.自我检测DAC答案:-3题型一根式与指数幂的互化课堂探究·素养提升名师导引:根式与分数指数幂的互化要求是什么?(①根指数?分数指数的分母;②被开方数(式)的指数?分数指数的分子) (1)根式与分数指数幂互化的关键是准确把握两种形式中相关数值的对应.①根指数?分数指数的分母;②被开方数(式)的指数?分数指数的分子.
(2)将含有多重根号的根式化为分数指数幂途径有两条:一是由里向外化为分数指数幂;二是由外向里化为分数指数幂.方法技巧题型二 利用指数幂的运算性质化简求值方法技巧 进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数为分数,化带分数为假分数进行运算,便于进行乘除、乘方、开方运算,以达到化繁为简的目的. 题型三 附加条件的幂的求值问题(2)将a+a-1=7两边平方,得a2+a-2+2=49,
所以a2+a-2=47.方法技巧 条件求值问题的基本步骤是先找条件和所求之间的关系,然后进行化简,最后代值运算,求值过程中要注意平方差公式、立方差公式以及一元二次方程中根与系数关系的灵活应用.题型四易错辨析——忽略 有意义出错谢谢观赏!
