2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.1.2指数函数及其性质第一课时指数函数的图象及性质课件新人教A版必修1(33张)
文档属性
| 名称 | 2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.1.2指数函数及其性质第一课时指数函数的图象及性质课件新人教A版必修1(33张) |  | |
| 格式 | zip | ||
| 文件大小 | 975.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 21:29:00 | ||
图片预览






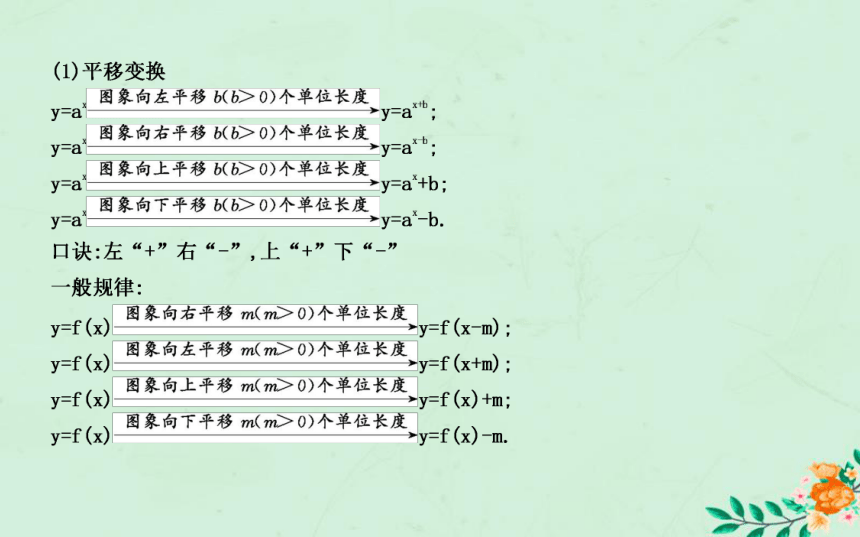




文档简介
课件33张PPT。2.1.2 指数函数及其性质
第一课时 指数函数的图象及性质目标导航新知探求课堂探究新知探求·素养养成想一想 1:导入二中两个对应能构成函数吗?
(能)想一想 2:这两个函数有什么特点?
(底数是常数,指数是自变量)知识探究1.指数函数的定义
函数 叫做指数函数,其中x是自变量,函数的定义域是R.
探究1:指数函数的解析式有何特征?
答案:指数函数的解析式具有以下特征:
(1)底数a>0,且为不等于1的常数,也不含有自变量x;
(2)指数位置是自变量x,且x的系数是1;
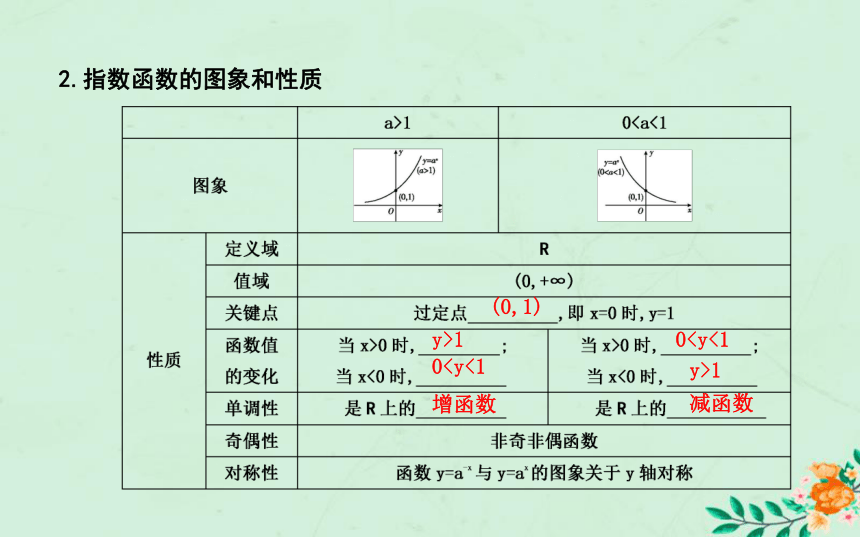
(3)ax的系数是1.y=ax(a>0,且a≠1)2.指数函数的图象和性质y>101增函数减函数(0,1)探究2:指数函数图象不可能出现在第几象限?
答案:指数函数图象只出现在第一、二象限,不可能出现在第三、四象限.
【拓展延伸】
1.指数函数y=ax(a>0,a≠1)的图象变换
函数的图象是直观表示函数的一种方法,函数的很多性质都可以从图象上一览无余,数形结合就是图形与代数方法紧密结合的一种数学思想.指数函数的图象通过平移、翻转等变换可得出一般函数的图象.利用函数的图象,能较简捷地解答一些与函数性质有关的问题.(2)对称规律
函数y=ax的图象与y=a-x的图象关于y轴对称,函数y=ax的图象与y=-ax的图象关于x轴对称,函数y=ax的图象与y=-a-x的图象关于坐标原点对称.
2.与指数函数有关的复合函数
与指数函数有关的复合函数主要包括形如y=af(x)和y=f(ax)的函数.
(1)与指数函数有关的复合函数的定义域、值域的求法
①函数y=af(x)的定义域与f(x)的定义域相同;
②求函数y=af(x)的值域,需先确定f(x)的值域,再根据指数函数y=ax的单调性确定函数y=af(x)的值域;
③求函数y=f(ax)的定义域,需先确定y=f(u)的定义域,即u的取值范围,亦即u=ax的值域,由此构造关于x的不等式(组),确定x的取值范围,得y=f(ax)的定义域;
④求函数y=f(ax)的值域,需先利用函数u=ax的单调性确定其值域,即u的取值范围,再确定函数y=f(u)的值域,即为y=f(ax)的值域.(2)与指数函数有关的复合函数的单调性
①形如y=af(x)的函数的单调性的判断方法:当a>1时,函数u=f(x)的单调增(减)区间即为函数y=af(x)的单调增(减)区间;当0②形如y=f(ax)的函数的单调性的判断方法:通过内层函数u=ax的取值范围确定外层函数y=f(u)的定义域,在此定义域内讨论外层函数的单调区间,再根据复合函数“同增异减”的法则确定复合函数的单调区间.自我检测BB1.(概念)下列以x为自变量的函数中,是指数函数的是( )
(A)y=(-5)x (B)y=ex(e≈2.718 28)
(C)y=-5x (D)y=πx+2B3.(单调性)指数函数f(x)=ax(a>0且a≠1)在R上是增函数,则a的取值范围是( )
(A)a>1 (B)a>2
(C)00且a≠1)的图象恒过定点,它的坐标为 .?题型一 指数函数的概念课堂探究·素养提升解析:④为指数函数.
①中底数-8<0,
所以不是指数函数.
②中指数不是自变量x,而是x的函数,
所以不是指数函数;
③中底数a,只有规定a>0且a≠1时,才是指数函数;
⑤中3x前的系数是2,而不是1,
所以不是指数函数.故选A. 判断一个函数为指数函数只需判定解析式符合y=ax(a>0且a≠1)结构前系数为1,指数为自变量x.方法技巧解:只有(4),(6)是指数函数,因它们满足指数函数的定义;(1)中解析式可变形为y=2x·22=4·2x,不满足指数函数的形式;(2)中底数为负,所以不是;(3)中解析式中多一负号,所以不是;(5)中指数为常数,所以不是;(6)中令b= a-1,则y=bx,b>0且b≠1,所以是.即时训练1-1:在下列的关系式中,哪些不是指数函数,为什么?
(1)y=2x+2;(2)y=(-2)x;(3)y=-2x;(4)y=πx;
(5)y=x2;(6)y=(a-1)x(a>1,且a≠2).解:②不是指数函数,因为自变量不在指数的位置上;③不是指数函数;④中底数-4<0,故不是指数函数;⑥中指数不是自变量x;⑦中底数x不是常数.故指数函数有①⑤⑧.题型二 指数函数的图象特征解析:法一 由于在第一象限内,指数函数符合底数越大,图象越高的规律且①②为减函数,③④为增函数,所以b法二 作直线x=1,与四个图象分别交于A,B,C,D四点,则A(1,a),B(1,b), C(1,c),D(1,d),由图可知b(A)a(C)1(1)由第一象限内“底大图高”的规律判断.
(2)取特殊值x=1得函数值的大小即底数大小进行判断.解析:(1)当a>0且a≠1时,总有f(2)=a2-2-3=a0-3=1-3=-2,所以函数f(x)=ax-2-3必过定点(2,-2).
(2)当x>0时,f(x)=ax,由于a>1,函数是增函数;当x<0时,f(x)=-ax,与f(x)=ax(x<0)关于x轴对称,只有③符合.
答案:(1)(2,-2) (2)③即时训练2-1:(1)当a>0且a≠1时,函数f(x)=ax-2-3必过定点 ;?题型三 与指数函数有关的定义域、值域问题(3)y=4x-4·2x+1.规范解答:(3)函数的定义域为R.………………………………9分
记t=2x>0.则y=t2-4t+1=(t-2)2-3.
故当t=2,即2x=2,
解得x=1时,y取得最小值-3.………………………11分
所以函数的值域为[-3,+∞).………………………12分方法技巧 函数y=af(x)的定义域与值域的求法
(1)形如y=af(x)的函数的定义域就是f(x)的定义域.
(2)形如y=af(x)的值域,应先求出f(x)的值域,再由函数的单调性求出af(x)的值域.若a的取值范围不确定,则需对a进行分类讨论.
(3)形如y=f(ax)的值域,要先求出u=ax的值域,再结合y=f(u)确定出y=f(ax)的值域.即时训练3-1:若函数f(x)=ax-1(a>0,a≠1)的定义域和值域都是[0,2],求实数a的值.解析:函数f(x)=ax(a>0且a≠1)在(0,2)内的值域是(1,a2),
由于指数函数是单调函数,则有a>1,
由底数大于1指数函数的图象上升,且在x轴上面,可知B正确.故选B.【备用例3】 已知函数f(x)=ax(a>0且a≠1)在(0,2)内的值域是(1,a2),则函数y=f(x)的图象大致是( )题型四 易错辨析——忽略函数的值域致错纠错:忽略了指数函数的值域(0,+∞)这个隐含条件.谢谢观赏!
第一课时 指数函数的图象及性质目标导航新知探求课堂探究新知探求·素养养成想一想 1:导入二中两个对应能构成函数吗?
(能)想一想 2:这两个函数有什么特点?
(底数是常数,指数是自变量)知识探究1.指数函数的定义
函数 叫做指数函数,其中x是自变量,函数的定义域是R.
探究1:指数函数的解析式有何特征?
答案:指数函数的解析式具有以下特征:
(1)底数a>0,且为不等于1的常数,也不含有自变量x;
(2)指数位置是自变量x,且x的系数是1;
(3)ax的系数是1.y=ax(a>0,且a≠1)2.指数函数的图象和性质y>10
答案:指数函数图象只出现在第一、二象限,不可能出现在第三、四象限.
【拓展延伸】
1.指数函数y=ax(a>0,a≠1)的图象变换
函数的图象是直观表示函数的一种方法,函数的很多性质都可以从图象上一览无余,数形结合就是图形与代数方法紧密结合的一种数学思想.指数函数的图象通过平移、翻转等变换可得出一般函数的图象.利用函数的图象,能较简捷地解答一些与函数性质有关的问题.(2)对称规律
函数y=ax的图象与y=a-x的图象关于y轴对称,函数y=ax的图象与y=-ax的图象关于x轴对称,函数y=ax的图象与y=-a-x的图象关于坐标原点对称.
2.与指数函数有关的复合函数
与指数函数有关的复合函数主要包括形如y=af(x)和y=f(ax)的函数.
(1)与指数函数有关的复合函数的定义域、值域的求法
①函数y=af(x)的定义域与f(x)的定义域相同;
②求函数y=af(x)的值域,需先确定f(x)的值域,再根据指数函数y=ax的单调性确定函数y=af(x)的值域;
③求函数y=f(ax)的定义域,需先确定y=f(u)的定义域,即u的取值范围,亦即u=ax的值域,由此构造关于x的不等式(组),确定x的取值范围,得y=f(ax)的定义域;
④求函数y=f(ax)的值域,需先利用函数u=ax的单调性确定其值域,即u的取值范围,再确定函数y=f(u)的值域,即为y=f(ax)的值域.(2)与指数函数有关的复合函数的单调性
①形如y=af(x)的函数的单调性的判断方法:当a>1时,函数u=f(x)的单调增(减)区间即为函数y=af(x)的单调增(减)区间;当0
(A)y=(-5)x (B)y=ex(e≈2.718 28)
(C)y=-5x (D)y=πx+2B3.(单调性)指数函数f(x)=ax(a>0且a≠1)在R上是增函数,则a的取值范围是( )
(A)a>1 (B)a>2
(C)0
①中底数-8<0,
所以不是指数函数.
②中指数不是自变量x,而是x的函数,
所以不是指数函数;
③中底数a,只有规定a>0且a≠1时,才是指数函数;
⑤中3x前的系数是2,而不是1,
所以不是指数函数.故选A. 判断一个函数为指数函数只需判定解析式符合y=ax(a>0且a≠1)结构前系数为1,指数为自变量x.方法技巧解:只有(4),(6)是指数函数,因它们满足指数函数的定义;(1)中解析式可变形为y=2x·22=4·2x,不满足指数函数的形式;(2)中底数为负,所以不是;(3)中解析式中多一负号,所以不是;(5)中指数为常数,所以不是;(6)中令b= a-1,则y=bx,b>0且b≠1,所以是.即时训练1-1:在下列的关系式中,哪些不是指数函数,为什么?
(1)y=2x+2;(2)y=(-2)x;(3)y=-2x;(4)y=πx;
(5)y=x2;(6)y=(a-1)x(a>1,且a≠2).解:②不是指数函数,因为自变量不在指数的位置上;③不是指数函数;④中底数-4<0,故不是指数函数;⑥中指数不是自变量x;⑦中底数x不是常数.故指数函数有①⑤⑧.题型二 指数函数的图象特征解析:法一 由于在第一象限内,指数函数符合底数越大,图象越高的规律且①②为减函数,③④为增函数,所以b
(2)取特殊值x=1得函数值的大小即底数大小进行判断.解析:(1)当a>0且a≠1时,总有f(2)=a2-2-3=a0-3=1-3=-2,所以函数f(x)=ax-2-3必过定点(2,-2).
(2)当x>0时,f(x)=ax,由于a>1,函数是增函数;当x<0时,f(x)=-ax,与f(x)=ax(x<0)关于x轴对称,只有③符合.
答案:(1)(2,-2) (2)③即时训练2-1:(1)当a>0且a≠1时,函数f(x)=ax-2-3必过定点 ;?题型三 与指数函数有关的定义域、值域问题(3)y=4x-4·2x+1.规范解答:(3)函数的定义域为R.………………………………9分
记t=2x>0.则y=t2-4t+1=(t-2)2-3.
故当t=2,即2x=2,
解得x=1时,y取得最小值-3.………………………11分
所以函数的值域为[-3,+∞).………………………12分方法技巧 函数y=af(x)的定义域与值域的求法
(1)形如y=af(x)的函数的定义域就是f(x)的定义域.
(2)形如y=af(x)的值域,应先求出f(x)的值域,再由函数的单调性求出af(x)的值域.若a的取值范围不确定,则需对a进行分类讨论.
(3)形如y=f(ax)的值域,要先求出u=ax的值域,再结合y=f(u)确定出y=f(ax)的值域.即时训练3-1:若函数f(x)=ax-1(a>0,a≠1)的定义域和值域都是[0,2],求实数a的值.解析:函数f(x)=ax(a>0且a≠1)在(0,2)内的值域是(1,a2),
由于指数函数是单调函数,则有a>1,
由底数大于1指数函数的图象上升,且在x轴上面,可知B正确.故选B.【备用例3】 已知函数f(x)=ax(a>0且a≠1)在(0,2)内的值域是(1,a2),则函数y=f(x)的图象大致是( )题型四 易错辨析——忽略函数的值域致错纠错:忽略了指数函数的值域(0,+∞)这个隐含条件.谢谢观赏!
