2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.2.1对数与对数运算第二课时对数的运算课件新人教A版必修1(33张)
文档属性
| 名称 | 2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.2.1对数与对数运算第二课时对数的运算课件新人教A版必修1(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 00:00:00 | ||
图片预览











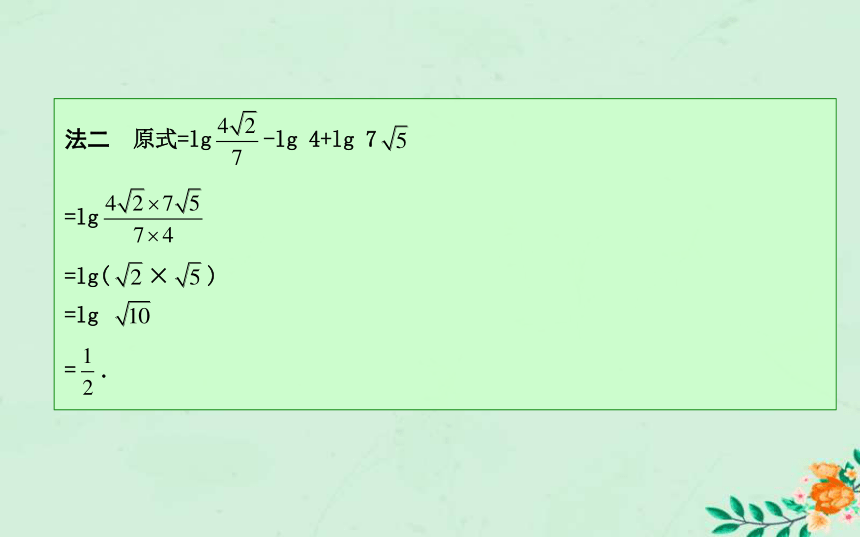
文档简介
课件33张PPT。第二课时 对数的运算目标导航新知探求课堂探究新知探求·素养养成【情境导学】
导入一 问题1:指数运算有哪些性质?
答案:若a,b>0,且a≠1,b≠1,r,s∈R,
则ar·as=ar+s;
arbr=(ab)r;
(ar)s=ars.
问题2:指数式ax=b对应的对数式是什么?
答案:x=logab.导入二 求下列对数的值:
①log24;②log28;③log232;④log832.
解:①设log24=x,则2x=4,所以x=2,即log24=2;
②设log28=x,则2x=8,所以x=3,即log28=3;
③设log232=x,则2x=32,所以x=5,即log232=5;想一想 导入二中①②③之间存在什么运算关系?知识探究1.对数的运算性质
如果a>0,且a≠1,M>0,N>0,那么:
(1)loga (M·N)= ;
(2)loga = ;
(3)loga Mn= (n∈R).
探究1:loga(MN)=logaM+logaN是否成立?
答案:不一定,当M>0且N>0时,该式成立,当M<0,N<0时,该式不成立.logaM+logaNlogaM-logaNnlogaM【拓展延伸】
与对数有关的方程的求解
与对数有关的方程主要有三类:
第一类是形如关于x的方程logaf(x)=b(a>0,且a≠1),通常将其转化为指数式f(x)=ab,这样解关于x的方程f(x)=ab即可,最后要注意验根.
第二类是形如关于x的方程logaf(x)=logag(x)(a>0,且a≠1),通常将其转化为求方程f(x)=g(x)的解即可,最后要注意验根.
第三类是形如关于x的方程f(logax)=0(a>0,且a≠1),通常利用换元法,设logax=t,转化为解方程f(t)=0得t=p的值,再解方程logax=p,化为指数式,则x=ap,最后要注意验根.自我检测BD1.(运算性质)log42-log48等于( )
(A)-2 (B)-1
(C)1 (D)2
2.(运算性质)log35-log345等于( )
(A)1 (B)-1
(C)2 (D)-2A答案:14.(换底公式)log816= .?5.(换底公式)log23·log34·log45·log52= .?题型一 对数运算性质的应用课堂探究·素养提升解:(2)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2
=2lg 10+(lg 5+lg 2)2
=2+(lg 10)2=2+1=3. (1)本题主要考查对数式的化简与计算.解决这类问题一般有两种思路:一是将式中真数的积、商、幂、方根运用对数的运算性质将它们化为对数的和、差、积、商,然后化简求值;二是将式中对数的和、差、积、商逆用对数的运算性质化为真数的积、商、幂、方根,然后化简求值.
(2)对数计算问题中,涉及lg 2,lg 5时,常利用lg 2+lg 5=1及lg 2=1- lg 5,lg 5=1-lg 2等解题.方法技巧(2)原式=lg 5(3lg 2+3)+3(lg 2)2-lg 6+lg 6-2
=3lg 5·lg 2+3lg 5+3(lg 2)2-2
=3lg 2(lg 5+lg 2)+3lg 5-2
=3lg 2+3lg 5-2=3(lg 2+lg 5)-2=1.解:(1)原式=2log32-(log332-log39)+3log32-3=2log32-5log32+2+3log32-3=-1.题型二 换底公式的应用【例2】 计算:(1)log1627log8132;(2)(log32+log92)(log43+log83).方法技巧 应用换底公式时,(1)一般都换成以10为底的对数.(2)根据情况找一个底数或真数的因子作为底.(2)已知log627=a,试用a表示log1816.题型三 与对数有关的方程问题【例3】 解方程:(1)log5(2x+1)=log5(x2-2);
(2)(lg x)2+lg x3-10=0.解:(1)由log5(2x+1)=log5(x2-2)得2x+1=x2-2,
即x2-2x-3=0,解得x=-1或x=3.
检验:当x=-1时,2x+1<0,舍去;
当x=3时,2x+1>0,x2-2>0.故x=3.
(2)原方程整理得(lg x)2+3lg x-10=0,
即(lg x+5)(lg x-2)=0,所以lg x=-5或lg x=2,
解得x=10-5或x=102,
经检验知,x=10-5,x=102都是原方程的解.方法技巧 简单的对数方程及其解法(2)lg x+2log10xx=2.【备用例3】 已知f(x)=x2+(lg a+2)x+lg b,f(-1)=-2,方程f(x)=2x至多有一个实根,求实数a,b的值.题型四易错辨析——忽视对数的意义致误解:因为lg(x+1)+lg x=lg[x(x+1)]=lg 6,所以x(x+1)=6,解得x=2或x=-3,经检验x=-3不符合题意,所以x=2.即时训练4-1:解方程lg(x+1)+lg x=lg 6.谢谢观赏!
导入一 问题1:指数运算有哪些性质?
答案:若a,b>0,且a≠1,b≠1,r,s∈R,
则ar·as=ar+s;
arbr=(ab)r;
(ar)s=ars.
问题2:指数式ax=b对应的对数式是什么?
答案:x=logab.导入二 求下列对数的值:
①log24;②log28;③log232;④log832.
解:①设log24=x,则2x=4,所以x=2,即log24=2;
②设log28=x,则2x=8,所以x=3,即log28=3;
③设log232=x,则2x=32,所以x=5,即log232=5;想一想 导入二中①②③之间存在什么运算关系?知识探究1.对数的运算性质
如果a>0,且a≠1,M>0,N>0,那么:
(1)loga (M·N)= ;
(2)loga = ;
(3)loga Mn= (n∈R).
探究1:loga(MN)=logaM+logaN是否成立?
答案:不一定,当M>0且N>0时,该式成立,当M<0,N<0时,该式不成立.logaM+logaNlogaM-logaNnlogaM【拓展延伸】
与对数有关的方程的求解
与对数有关的方程主要有三类:
第一类是形如关于x的方程logaf(x)=b(a>0,且a≠1),通常将其转化为指数式f(x)=ab,这样解关于x的方程f(x)=ab即可,最后要注意验根.
第二类是形如关于x的方程logaf(x)=logag(x)(a>0,且a≠1),通常将其转化为求方程f(x)=g(x)的解即可,最后要注意验根.
第三类是形如关于x的方程f(logax)=0(a>0,且a≠1),通常利用换元法,设logax=t,转化为解方程f(t)=0得t=p的值,再解方程logax=p,化为指数式,则x=ap,最后要注意验根.自我检测BD1.(运算性质)log42-log48等于( )
(A)-2 (B)-1
(C)1 (D)2
2.(运算性质)log35-log345等于( )
(A)1 (B)-1
(C)2 (D)-2A答案:14.(换底公式)log816= .?5.(换底公式)log23·log34·log45·log52= .?题型一 对数运算性质的应用课堂探究·素养提升解:(2)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2
=2lg 10+(lg 5+lg 2)2
=2+(lg 10)2=2+1=3. (1)本题主要考查对数式的化简与计算.解决这类问题一般有两种思路:一是将式中真数的积、商、幂、方根运用对数的运算性质将它们化为对数的和、差、积、商,然后化简求值;二是将式中对数的和、差、积、商逆用对数的运算性质化为真数的积、商、幂、方根,然后化简求值.
(2)对数计算问题中,涉及lg 2,lg 5时,常利用lg 2+lg 5=1及lg 2=1- lg 5,lg 5=1-lg 2等解题.方法技巧(2)原式=lg 5(3lg 2+3)+3(lg 2)2-lg 6+lg 6-2
=3lg 5·lg 2+3lg 5+3(lg 2)2-2
=3lg 2(lg 5+lg 2)+3lg 5-2
=3lg 2+3lg 5-2=3(lg 2+lg 5)-2=1.解:(1)原式=2log32-(log332-log39)+3log32-3=2log32-5log32+2+3log32-3=-1.题型二 换底公式的应用【例2】 计算:(1)log1627log8132;(2)(log32+log92)(log43+log83).方法技巧 应用换底公式时,(1)一般都换成以10为底的对数.(2)根据情况找一个底数或真数的因子作为底.(2)已知log627=a,试用a表示log1816.题型三 与对数有关的方程问题【例3】 解方程:(1)log5(2x+1)=log5(x2-2);
(2)(lg x)2+lg x3-10=0.解:(1)由log5(2x+1)=log5(x2-2)得2x+1=x2-2,
即x2-2x-3=0,解得x=-1或x=3.
检验:当x=-1时,2x+1<0,舍去;
当x=3时,2x+1>0,x2-2>0.故x=3.
(2)原方程整理得(lg x)2+3lg x-10=0,
即(lg x+5)(lg x-2)=0,所以lg x=-5或lg x=2,
解得x=10-5或x=102,
经检验知,x=10-5,x=102都是原方程的解.方法技巧 简单的对数方程及其解法(2)lg x+2log10xx=2.【备用例3】 已知f(x)=x2+(lg a+2)x+lg b,f(-1)=-2,方程f(x)=2x至多有一个实根,求实数a,b的值.题型四易错辨析——忽视对数的意义致误解:因为lg(x+1)+lg x=lg[x(x+1)]=lg 6,所以x(x+1)=6,解得x=2或x=-3,经检验x=-3不符合题意,所以x=2.即时训练4-1:解方程lg(x+1)+lg x=lg 6.谢谢观赏!
