2018_2019学年高中数学第二章基本初等函数(Ⅰ)章末总结课件新人教A版必修1(30张)
文档属性
| 名称 | 2018_2019学年高中数学第二章基本初等函数(Ⅰ)章末总结课件新人教A版必修1(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 21:34:37 | ||
图片预览










文档简介
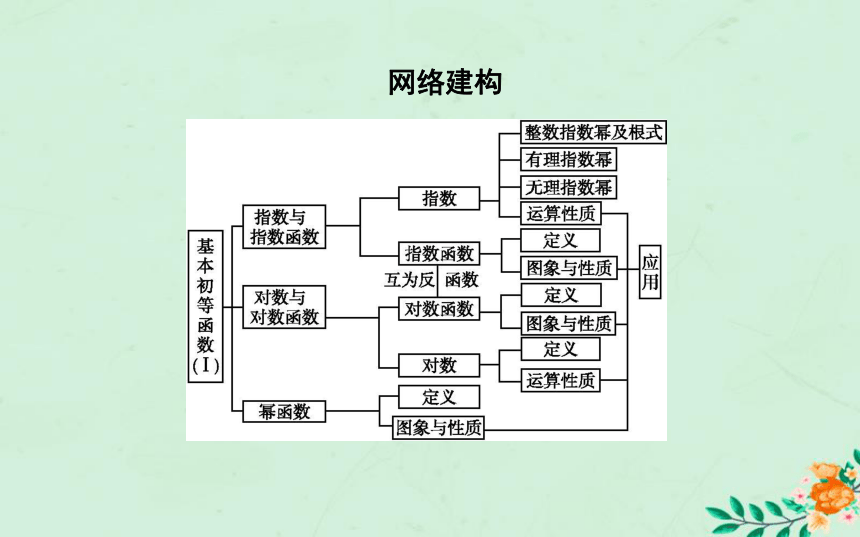
课件30张PPT。章末总结网络建构知识辨析判断下列说法是否正确(请在括号中填“√”或“×”)×√2.指数函数的图象一定在x轴的上方.( )
3.y=3·2x是指数函数.( )
4.任何指数式都可以化为对数式.( )
5.logaxy=logax+logay(a>0且a≠1).( )
6.y=x2与y=log2x互为反函数.( )
7.互为反函数的两个函数图象关于y=x对称.( )
8.幂函数图象可在直角坐标系第四象限出现.( )
9.对数函数图象一定在y轴右侧.( )××××√×√题型探究真题体验题型探究·素养提升一、指数、对数的运算
【典例1】 计算下列各题:规律方法 (1)指数式的运算:注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算.
(2)对数式的运算:①注意公式应用过程中范围的变化,前后要等价.②熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.二、指数函数、对数函数、幂函数的图象和性质(A)(1,1) (B)(1,0) (C)(2,1) (D)(2,0)答案:(1)C 解析:(2)①可举偶函数y=x-2,则它的图象与y轴不相交,故①错;答案:(2)②③规律方法 (1)根据函数解析式判断函数的相关性质,如定义域、值域、单调性、奇偶性等进行判断,也可根据函数性质进行排除干扰项而得到正确结果.
(2)根据函数解析式特征确定相关的基本初等函数,如指数函数、对数函数、幂函数等,然后确定其平移变化的方向,从而判断函数图象.
(3)指数函数与对数函数图象经过定点的实质是a0=1,loga1=0.
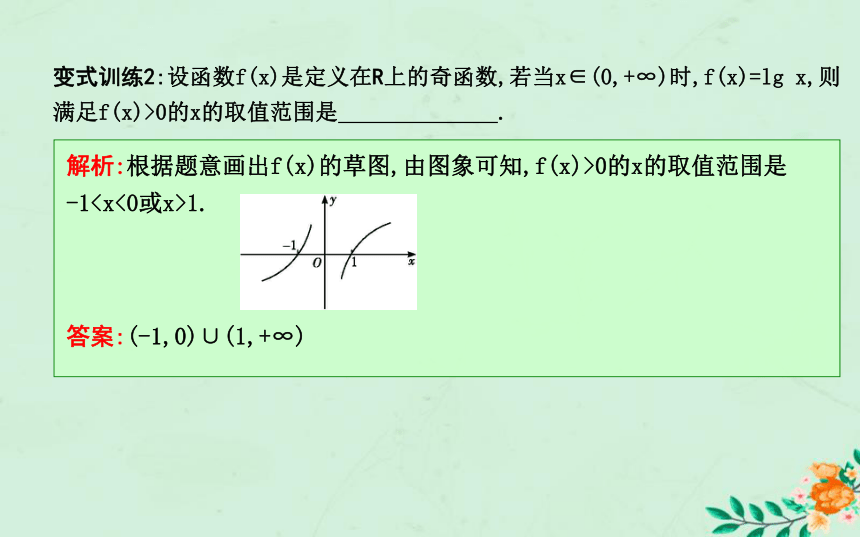
(4)指数函数与对数函数都具有单调性,当01时,两者都是递增函数.变式训练2:设函数f(x)是定义在R上的奇函数,若当x∈(0,+∞)时,f(x)=lg x,则满足f(x)>0的x的取值范围是 .?解析:根据题意画出f(x)的草图,由图象可知,f(x)>0的x的取值范围是
-11.答案:(-1,0)∪(1,+∞)三、比较大小
【典例3】 (1)设a=40.1,b=log30.1,c=0.50.1,则( )
(A)a>b>c (B)a>c>b
(C)b>a>c (D)b>c>a(A)c(C)b1,b=log30.1<0,0c>b.故选B.(3)(2018·海南中学高一期中)设a=log0.50.8,b=log1.10.8,c=1.10.8,则a,b,c的大小关系为( )
(A)a(C)bb=log1.10.81.10=1,
所以b(2)当两个数都是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.
(3)比较多个数的大小时,先利用“0”“1”作为分界点,然后在各部分内再利用函数性质比较大小.
(4)含参数的问题,要根据参数的取值进行分类讨论.四、幂函数、指数函数、对数函数的综合(2)求f(x)的最小值.规律方法 研究指数函数与对数函数及幂函数的综合问题,需灵活利用换元法将复合函数分解为两个简单函数,进而将问题转化为常见函数问题来处理.但要注意函数定义域的变化.(1)若f(x)=2,求x的值;(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.五、易错辨析——忽视真数的范围致误纠错:错解中忽视了对数真数应大于0的条件.真题体验·素养升级(A)b(C)bb>0,0(A)logac(C)accbB3.(2017·全国Ⅰ卷)设x,y,z为正数,且2x=3y=5z,则( )
(A)2x<3y<5z (B)5z<2x<3y
(C)3y<5z<2x (D)3y<2x<5zD4.(2017·北京卷)已知函数f(x)=3x-( )x,则f(x)( )
(A)是奇函数,且在R上是增函数
(B)是偶函数,且在R上是增函数
(C)是奇函数,且在R上是减函数
(D)是偶函数,且在R上是减函数A5.(2017·天津卷)已知奇函数f(x)在R上是增函数,g(x)=xf(x).若a=g(-log25.1),
b=g(20.8),c=g(3),则a,b,c的大小关系为( )
(A)a(C)b=g(log25.1).
因为f(x)在R上是增函数,可设0则f(x1)从而x1f(x1)所以g(x)在(0,+∞)上亦为增函数.
又log25.1>0,20.8>0,3>0,且20.8<21=log24所以3>log25.1>20.8>0,所以c>a>b.故选C.6.(2016·浙江卷)已知a>b>1.若logab+logba= ,ab=ba,则a= ,
b= .?答案:4 2谢谢观赏!
3.y=3·2x是指数函数.( )
4.任何指数式都可以化为对数式.( )
5.logaxy=logax+logay(a>0且a≠1).( )
6.y=x2与y=log2x互为反函数.( )
7.互为反函数的两个函数图象关于y=x对称.( )
8.幂函数图象可在直角坐标系第四象限出现.( )
9.对数函数图象一定在y轴右侧.( )××××√×√题型探究真题体验题型探究·素养提升一、指数、对数的运算
【典例1】 计算下列各题:规律方法 (1)指数式的运算:注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算.
(2)对数式的运算:①注意公式应用过程中范围的变化,前后要等价.②熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.二、指数函数、对数函数、幂函数的图象和性质(A)(1,1) (B)(1,0) (C)(2,1) (D)(2,0)答案:(1)C 解析:(2)①可举偶函数y=x-2,则它的图象与y轴不相交,故①错;答案:(2)②③规律方法 (1)根据函数解析式判断函数的相关性质,如定义域、值域、单调性、奇偶性等进行判断,也可根据函数性质进行排除干扰项而得到正确结果.
(2)根据函数解析式特征确定相关的基本初等函数,如指数函数、对数函数、幂函数等,然后确定其平移变化的方向,从而判断函数图象.
(3)指数函数与对数函数图象经过定点的实质是a0=1,loga1=0.
(4)指数函数与对数函数都具有单调性,当0
-1
【典例3】 (1)设a=40.1,b=log30.1,c=0.50.1,则( )
(A)a>b>c (B)a>c>b
(C)b>a>c (D)b>c>a(A)c
(A)a
所以b
(3)比较多个数的大小时,先利用“0”“1”作为分界点,然后在各部分内再利用函数性质比较大小.
(4)含参数的问题,要根据参数的取值进行分类讨论.四、幂函数、指数函数、对数函数的综合(2)求f(x)的最小值.规律方法 研究指数函数与对数函数及幂函数的综合问题,需灵活利用换元法将复合函数分解为两个简单函数,进而将问题转化为常见函数问题来处理.但要注意函数定义域的变化.(1)若f(x)=2,求x的值;(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.五、易错辨析——忽视真数的范围致误纠错:错解中忽视了对数真数应大于0的条件.真题体验·素养升级(A)b
(A)2x<3y<5z (B)5z<2x<3y
(C)3y<5z<2x (D)3y<2x<5zD4.(2017·北京卷)已知函数f(x)=3x-( )x,则f(x)( )
(A)是奇函数,且在R上是增函数
(B)是偶函数,且在R上是增函数
(C)是奇函数,且在R上是减函数
(D)是偶函数,且在R上是减函数A5.(2017·天津卷)已知奇函数f(x)在R上是增函数,g(x)=xf(x).若a=g(-log25.1),
b=g(20.8),c=g(3),则a,b,c的大小关系为( )
(A)a
因为f(x)在R上是增函数,可设0
又log25.1>0,20.8>0,3>0,且20.8<21=log24
b= .?答案:4 2谢谢观赏!
