北师大七年级下《第五章生活中的轴对称》质量检测试卷含答案
文档属性
| 名称 | 北师大七年级下《第五章生活中的轴对称》质量检测试卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 126.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-01 07:49:28 | ||
图片预览

文档简介
本章质量评估
(时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
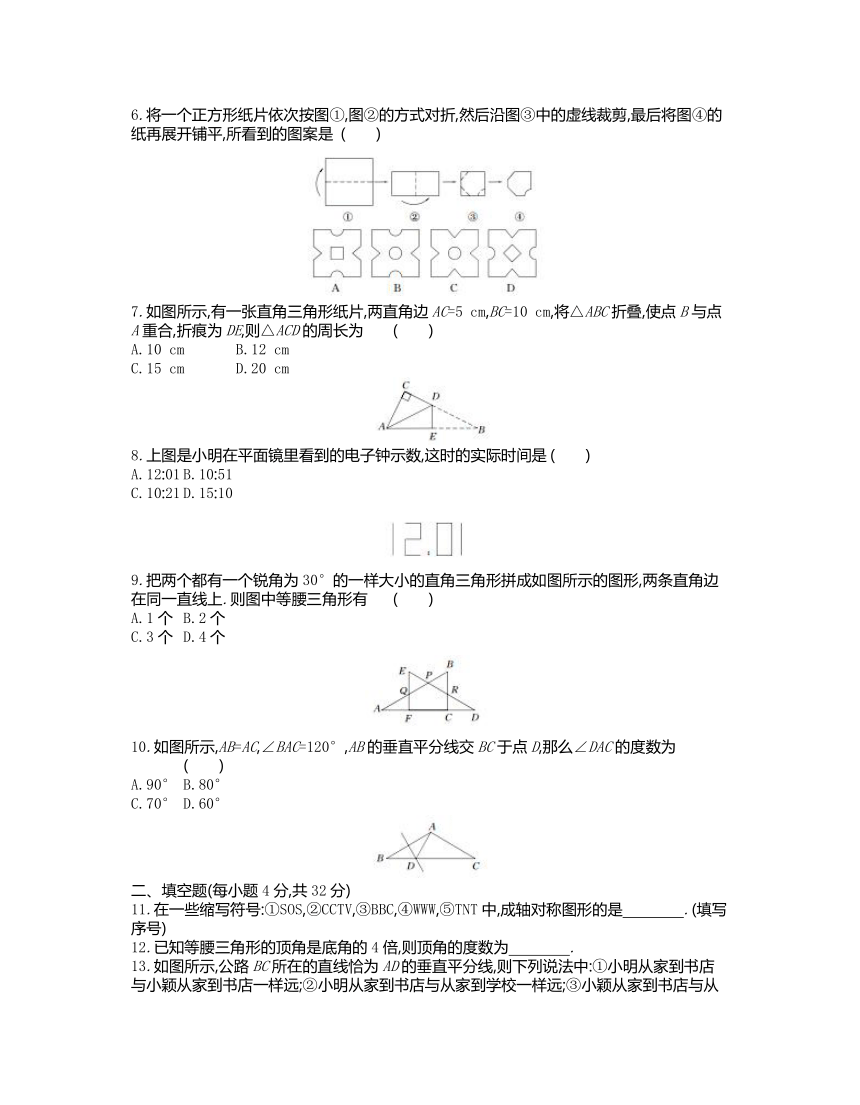
1.下列图形中,轴对称图形的个数是 ( )
A.4个 B.3个
C.2个 D.1个
2.如图所示,在永洁环保、绿色食品、节能、绿色环保四个标识中,是轴对称图形的是 ( )
A B C D
3.如图所示,将长方形ABCD纸片沿对角线BD折叠,使点C落在C'处,BC'交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)的个数是 ( )
A.5个 B.4个
C.3个 D.2个
4.下列说法中错误的是 ( )
A.两个关于某直线对称的图形一定能够完全重合
B.对称图形的对称点一定在对称轴的两侧
C.成轴对称的两个图形,其对应点的连线的垂直平分线是它们的对称轴
D.平面上两个能够完全重合的图形不一定关于某直线对称
5.如图所示,△AOD关于直线l进行轴对称变换后得到△BOC,下列说法中不正确的是 ( )
A.∠DAO=∠CBO,∠ADO=∠BCO
B.直线l垂直平分AB,CD
C.△AOD和△BOC均是等腰三角形
D.AD=BC,OD=OC
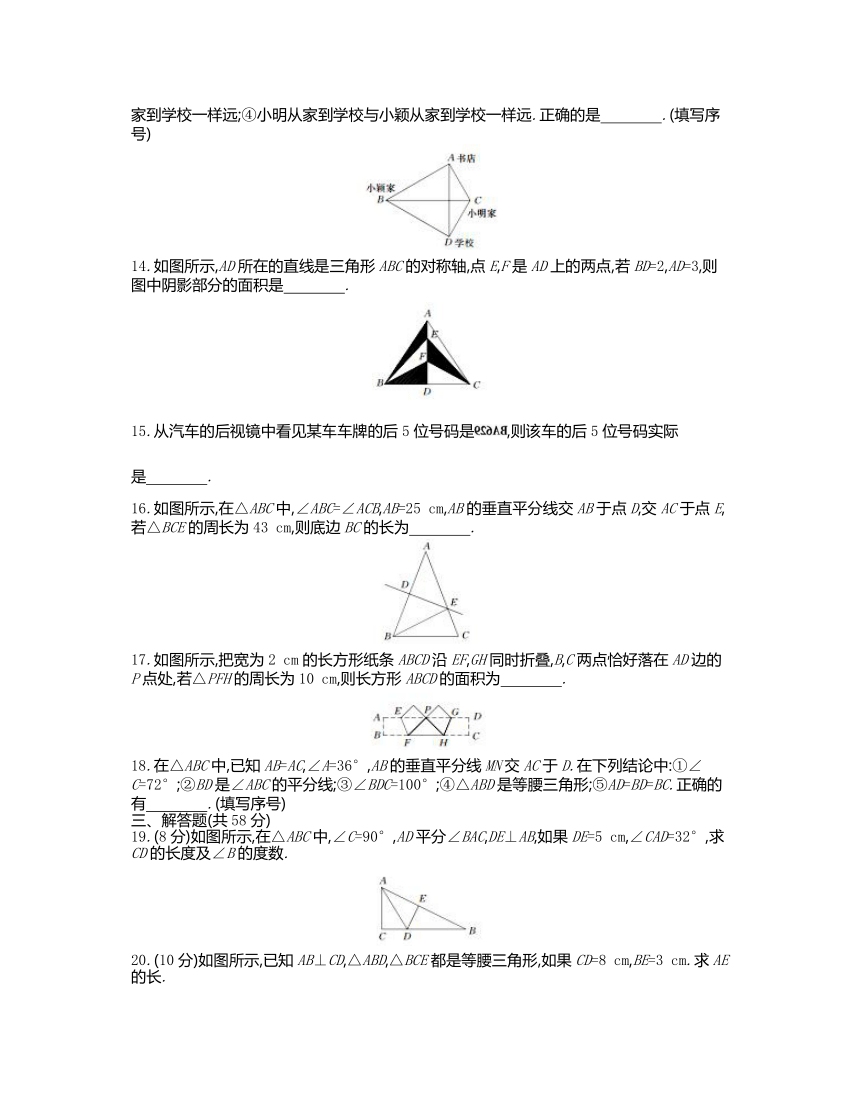
6.将一个正方形纸片依次按图①,图②的方式对折,然后沿图③中的虚线裁剪,最后将图④的纸再展开铺平,所看到的图案是 ( )
7.如图所示,有一张直角三角形纸片,两直角边AC=5 cm,BC=10 cm,将△ABC折叠,使点B与点A重合,折痕为DE,则△ACD的周长为 ( )
A.10 cm B.12 cm
C.15 cm D.20 cm
8.上图是小明在平面镜里看到的电子钟示数,这时的实际时间是 ( )
A.12:01 B.10:51
C.10:21 D.15:10
9.把两个都有一个锐角为30°的一样大小的直角三角形拼成如图所示的图形,两条直角边在同一直线上.则图中等腰三角形有 ( )
A.1个 B.2个
C.3个 D.4个
10.如图所示,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠DAC的度数为 ( )
A.90° B.80°
C.70° D.60°
二、填空题(每小题4分,共32分)
11.在一些缩写符号:①SOS,②CCTV,③BBC,④WWW,⑤TNT中,成轴对称图形的是 .(填写序号)?
12.已知等腰三角形的顶角是底角的4倍,则顶角的度数为 .?
13.如图所示,公路BC所在的直线恰为AD的垂直平分线,则下列说法中:①小明从家到书店与小颖从家到书店一样远;②小明从家到书店与从家到学校一样远;③小颖从家到书店与从家到学校一样远;④小明从家到学校与小颖从家到学校一样远.正确的是 .(填写序号)?
14.如图所示,AD所在的直线是三角形ABC的对称轴,点E,F是AD上的两点,若BD=2,AD=3,则图中阴影部分的面积是 .?
15.从汽车的后视镜中看见某车车牌的后5位号码是,则该车的后5位号码实际是 .?
16.如图所示,在△ABC中,∠ABC=∠ACB,AB=25 cm,AB的垂直平分线交AB于点D,交AC于点E,若△BCE的周长为43 cm,则底边BC的长为 .?
17.如图所示,把宽为2 cm的长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若△PFH的周长为10 cm,则长方形ABCD的面积为 .?
18.在△ABC中,已知AB=AC,∠A=36°,AB的垂直平分线MN交AC于D.在下列结论中:①∠C=72°;②BD是∠ABC的平分线;③∠BDC=100°;④△ABD是等腰三角形;⑤AD=BD=BC.正确的有 .(填写序号)?
三、解答题(共58分)
19.(8分)如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,如果DE=5 cm,∠CAD=32°,求CD的长度及∠B的度数.
20.(10分)如图所示,已知AB⊥CD,△ABD,△BCE都是等腰三角形,如果CD=8 cm,BE=3 cm.求AE的长.
21.(10分)如图所示,校园有两条路OA,OB,在交叉口附近有两块宣传牌C,D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置点P,并说明理由.
22.(10分)如图所示,在正方形网格上有一个△ABC.
(1)画△ABC关于直线MN的对称图形(不写画法);
(2)若网格上的每个小正方形的边长都为1,求△ABC的面积.
23.(10分)(1)观察图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;(小正方形的面积都相等)
(2)借助图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与图①~④的图案不能重合)
24.(10分)如图所示,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
【答案与解析】
1.B(解析:可利用轴对称图形的定义判断.)
2.B
3.A(解析:图中45°的角分别是∠CBC',∠ABE,∠AEB,∠C'ED,∠C'DE.)
4.B(解析:对称图形的对称点也可能在对称轴上.)
5.C(解析:△AOD和△BOC的形状不确定.)
6.D(解析:可动手操作,或空间想象.)
7.C(解析:由题意得AD=BD.故△ACD的周长=AC+CD+AD=AC+BC=15 cm.)
8.B(解析:镜子中看到的时刻的读数与实际时刻的读数关于镜面成轴对称.)
9.C(解析:等边三角形是特殊的等腰三角形,故等腰三角形有△EPQ,△BPR,△PAD.)
10.A(解析:可求得∠B=∠BAD=30°,故∠DAC=90°.)
11.③④
12.120°(解析:设底角的度数为x,则顶角的度数为4x,则有x+x+4x=180°.)
13.②③(解析:利用线段的垂直平分线的性质,可知②③正确.)
14.3(解析:利用转化思想,阴影部分的面积即为直角三角形ABD的面积.)
15.BA629(解析:这5位号码与其在镜子中所成的像关于镜面成轴对称.)
16.18 cm(解析:由BE+CE=AC=AB=25,可得BC=43- 25=18(cm).)
17.20 cm2(解析:根据轴对称的性质得BC的长即为△PFH的周长.)
18.①②④⑤(解析:∠ABC=∠C=∠BDC=72°,∠CBD=∠ABD=∠A=36°.)
19.解:因为AD平分∠BAC,DE⊥AB,DC⊥AC,所以CD=DE=5 cm.因为AD平分∠BAC,所以∠CAB=2∠CAD=2×32°=64°,所以∠B=90°- 64°=26°.
20.解:因为△ABD,△BCE都是等腰三角形,所以AB=BD,BC=BE.又因为BD=CD- BC,所以AB=CD- BC=CD- BE=8- 3=5(cm),所以AE=AB- BE=5- 3=2(cm).
21.解:如图所示.到∠AOB两边距离相等的点在这个角的平分线上,而到宣传牌C,D的距离相等的点在线段CD的垂直平分线上,故交点P即为所求.
22.解:(1)如图所示. (2)S△ABC=4×6- ×2×4- ×1×4- ×3×6=9.
23.解:(1)都是轴对称图形,它们的面积相等. (2)答案不唯一,如图所示.
24.解:(1)因为EF∥BC,所以∠AEF=∠B,∠AFE=∠C.又因为AB=AC,所以∠B=∠C,所以∠AEF=∠AFE,所以AE=AF,即△AEF是等腰三角形. (2)DE=DF.理由如下:方法一:因为AD是等腰三角形ABC的底边上的高,所以AD也是∠BAC的平分线.又因为△AEF是等腰三角形,所以AG是底边EF上的高和中线,所以AD⊥EF,GE=GF,所以AD是线段EF的垂直平分线,所以DE=DF.方法二:因为AD是等腰三角形ABC的底边上的高,所以BD=CD(三线合一).又因为点E,F分别是边AB,AC的中点,所以BE=CF,又因为∠B=∠C,所以△BDE≌△CDF(SAS),所以DE=DF.
(时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列图形中,轴对称图形的个数是 ( )
A.4个 B.3个
C.2个 D.1个
2.如图所示,在永洁环保、绿色食品、节能、绿色环保四个标识中,是轴对称图形的是 ( )
A B C D
3.如图所示,将长方形ABCD纸片沿对角线BD折叠,使点C落在C'处,BC'交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)的个数是 ( )
A.5个 B.4个
C.3个 D.2个
4.下列说法中错误的是 ( )
A.两个关于某直线对称的图形一定能够完全重合
B.对称图形的对称点一定在对称轴的两侧
C.成轴对称的两个图形,其对应点的连线的垂直平分线是它们的对称轴
D.平面上两个能够完全重合的图形不一定关于某直线对称
5.如图所示,△AOD关于直线l进行轴对称变换后得到△BOC,下列说法中不正确的是 ( )
A.∠DAO=∠CBO,∠ADO=∠BCO
B.直线l垂直平分AB,CD
C.△AOD和△BOC均是等腰三角形
D.AD=BC,OD=OC
6.将一个正方形纸片依次按图①,图②的方式对折,然后沿图③中的虚线裁剪,最后将图④的纸再展开铺平,所看到的图案是 ( )
7.如图所示,有一张直角三角形纸片,两直角边AC=5 cm,BC=10 cm,将△ABC折叠,使点B与点A重合,折痕为DE,则△ACD的周长为 ( )
A.10 cm B.12 cm
C.15 cm D.20 cm
8.上图是小明在平面镜里看到的电子钟示数,这时的实际时间是 ( )
A.12:01 B.10:51
C.10:21 D.15:10
9.把两个都有一个锐角为30°的一样大小的直角三角形拼成如图所示的图形,两条直角边在同一直线上.则图中等腰三角形有 ( )
A.1个 B.2个
C.3个 D.4个
10.如图所示,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠DAC的度数为 ( )
A.90° B.80°
C.70° D.60°
二、填空题(每小题4分,共32分)
11.在一些缩写符号:①SOS,②CCTV,③BBC,④WWW,⑤TNT中,成轴对称图形的是 .(填写序号)?
12.已知等腰三角形的顶角是底角的4倍,则顶角的度数为 .?
13.如图所示,公路BC所在的直线恰为AD的垂直平分线,则下列说法中:①小明从家到书店与小颖从家到书店一样远;②小明从家到书店与从家到学校一样远;③小颖从家到书店与从家到学校一样远;④小明从家到学校与小颖从家到学校一样远.正确的是 .(填写序号)?
14.如图所示,AD所在的直线是三角形ABC的对称轴,点E,F是AD上的两点,若BD=2,AD=3,则图中阴影部分的面积是 .?
15.从汽车的后视镜中看见某车车牌的后5位号码是,则该车的后5位号码实际是 .?
16.如图所示,在△ABC中,∠ABC=∠ACB,AB=25 cm,AB的垂直平分线交AB于点D,交AC于点E,若△BCE的周长为43 cm,则底边BC的长为 .?
17.如图所示,把宽为2 cm的长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若△PFH的周长为10 cm,则长方形ABCD的面积为 .?
18.在△ABC中,已知AB=AC,∠A=36°,AB的垂直平分线MN交AC于D.在下列结论中:①∠C=72°;②BD是∠ABC的平分线;③∠BDC=100°;④△ABD是等腰三角形;⑤AD=BD=BC.正确的有 .(填写序号)?
三、解答题(共58分)
19.(8分)如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,如果DE=5 cm,∠CAD=32°,求CD的长度及∠B的度数.
20.(10分)如图所示,已知AB⊥CD,△ABD,△BCE都是等腰三角形,如果CD=8 cm,BE=3 cm.求AE的长.
21.(10分)如图所示,校园有两条路OA,OB,在交叉口附近有两块宣传牌C,D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置点P,并说明理由.
22.(10分)如图所示,在正方形网格上有一个△ABC.
(1)画△ABC关于直线MN的对称图形(不写画法);
(2)若网格上的每个小正方形的边长都为1,求△ABC的面积.
23.(10分)(1)观察图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;(小正方形的面积都相等)
(2)借助图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与图①~④的图案不能重合)
24.(10分)如图所示,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
【答案与解析】
1.B(解析:可利用轴对称图形的定义判断.)
2.B
3.A(解析:图中45°的角分别是∠CBC',∠ABE,∠AEB,∠C'ED,∠C'DE.)
4.B(解析:对称图形的对称点也可能在对称轴上.)
5.C(解析:△AOD和△BOC的形状不确定.)
6.D(解析:可动手操作,或空间想象.)
7.C(解析:由题意得AD=BD.故△ACD的周长=AC+CD+AD=AC+BC=15 cm.)
8.B(解析:镜子中看到的时刻的读数与实际时刻的读数关于镜面成轴对称.)
9.C(解析:等边三角形是特殊的等腰三角形,故等腰三角形有△EPQ,△BPR,△PAD.)
10.A(解析:可求得∠B=∠BAD=30°,故∠DAC=90°.)
11.③④
12.120°(解析:设底角的度数为x,则顶角的度数为4x,则有x+x+4x=180°.)
13.②③(解析:利用线段的垂直平分线的性质,可知②③正确.)
14.3(解析:利用转化思想,阴影部分的面积即为直角三角形ABD的面积.)
15.BA629(解析:这5位号码与其在镜子中所成的像关于镜面成轴对称.)
16.18 cm(解析:由BE+CE=AC=AB=25,可得BC=43- 25=18(cm).)
17.20 cm2(解析:根据轴对称的性质得BC的长即为△PFH的周长.)
18.①②④⑤(解析:∠ABC=∠C=∠BDC=72°,∠CBD=∠ABD=∠A=36°.)
19.解:因为AD平分∠BAC,DE⊥AB,DC⊥AC,所以CD=DE=5 cm.因为AD平分∠BAC,所以∠CAB=2∠CAD=2×32°=64°,所以∠B=90°- 64°=26°.
20.解:因为△ABD,△BCE都是等腰三角形,所以AB=BD,BC=BE.又因为BD=CD- BC,所以AB=CD- BC=CD- BE=8- 3=5(cm),所以AE=AB- BE=5- 3=2(cm).
21.解:如图所示.到∠AOB两边距离相等的点在这个角的平分线上,而到宣传牌C,D的距离相等的点在线段CD的垂直平分线上,故交点P即为所求.
22.解:(1)如图所示. (2)S△ABC=4×6- ×2×4- ×1×4- ×3×6=9.
23.解:(1)都是轴对称图形,它们的面积相等. (2)答案不唯一,如图所示.
24.解:(1)因为EF∥BC,所以∠AEF=∠B,∠AFE=∠C.又因为AB=AC,所以∠B=∠C,所以∠AEF=∠AFE,所以AE=AF,即△AEF是等腰三角形. (2)DE=DF.理由如下:方法一:因为AD是等腰三角形ABC的底边上的高,所以AD也是∠BAC的平分线.又因为△AEF是等腰三角形,所以AG是底边EF上的高和中线,所以AD⊥EF,GE=GF,所以AD是线段EF的垂直平分线,所以DE=DF.方法二:因为AD是等腰三角形ABC的底边上的高,所以BD=CD(三线合一).又因为点E,F分别是边AB,AC的中点,所以BE=CF,又因为∠B=∠C,所以△BDE≌△CDF(SAS),所以DE=DF.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
