北师大七年级下《第二章相交线与平行线》质量检测试卷(含答案)
文档属性
| 名称 | 北师大七年级下《第二章相交线与平行线》质量检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 78.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 21:41:45 | ||
图片预览

文档简介
本章质量评估
(时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图所示,直线AB,CD相交于点E,DF∥AB.若∠AEC=100°,则∠D等于 ( )
A.70° B.80° C.90° D.100°
2.下列说法不正确的是 ( )
A.若两个相等的角有一组边平行,则另一组边也平行
B.两条直线相交,所成的两组对顶角的平分线互相垂直
C.两条平行线被第三条直线所截,同旁内角的平分线互相垂直
D.经过直线外一点,有且只有一条直线与已知直线平行
3.如图所示,直线a,b都和直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的有 ( )
A.①③ B.②④
C.①③④ D.①②③④
4.下列说法不正确的是 ( )
A.如果两条直线都和第三条直线平行,那么这两条直线也平行
B.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
C.两条直线被第三条直线所截,如果同位角互补,那么这两条直线平行
D.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
5.下列说法中正确的是 ( )
A.相等的两个角是对顶角
B.一条直线有且只有一条垂线
C.直线外一点与这条直线上的各点所连接的线段中,垂线段最短
D.一个角一定不等于它的余角
6.如图所示,直线l1∥l2,∠1=120°,则∠2的度数为 ( )
A.60° B.80° C.100° D.120°
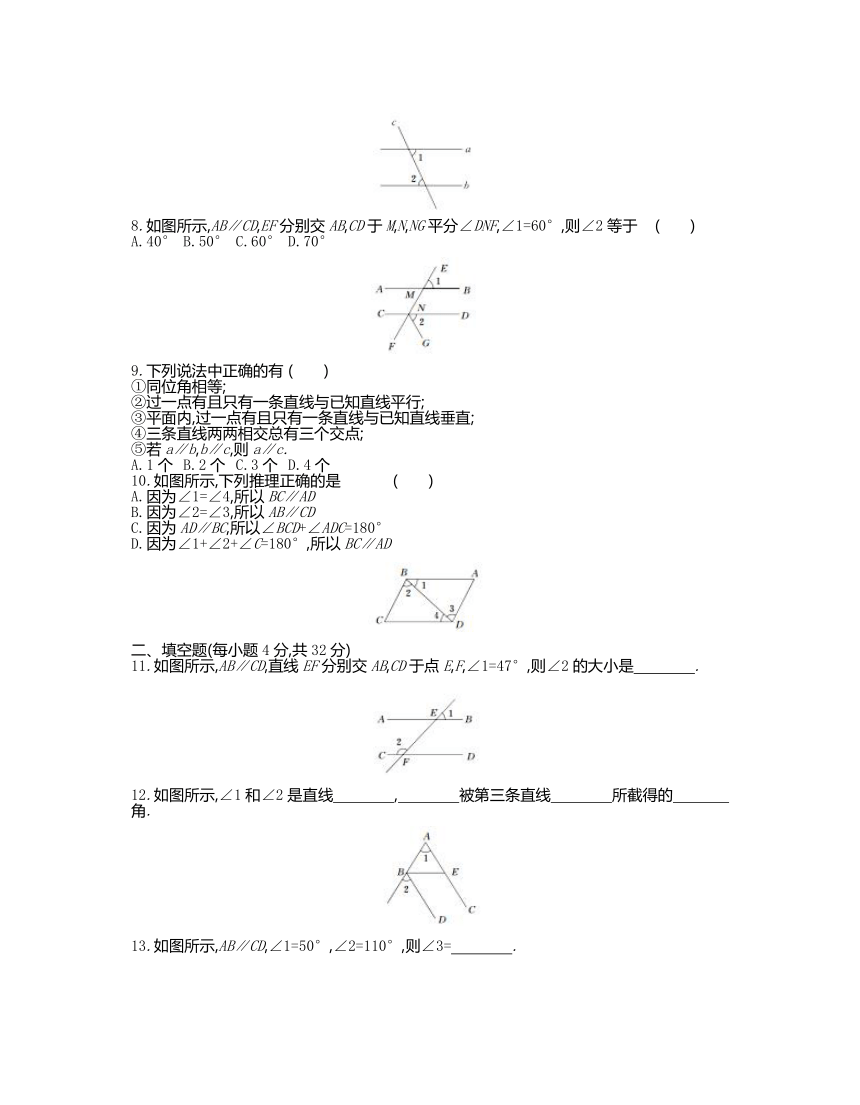
7.如图所示,已知直线a,b被直线c所截,且a∥b,∠1=65°,那么∠2等于 ( )
A.145° B.65° C.55° D.35°
8.如图所示,AB∥CD,EF分别交AB,CD于M,N,NG平分∠DNF,∠1=60°,则∠2等于 ( )
A.40° B.50° C.60° D.70°
9.下列说法中正确的有 ( )
①同位角相等;
②过一点有且只有一条直线与已知直线平行;
③平面内,过一点有且只有一条直线与已知直线垂直;
④三条直线两两相交总有三个交点;
⑤若a∥b,b∥c,则a∥c.
A.1个 B.2个 C.3个 D.4个
10.如图所示,下列推理正确的是 ( )
A.因为∠1=∠4,所以BC∥AD
B.因为∠2=∠3,所以AB∥CD
C.因为AD∥BC,所以∠BCD+∠ADC=180°
D.因为∠1+∠2+∠C=180°,所以BC∥AD
二、填空题(每小题4分,共32分)
11.如图所示,AB∥CD,直线EF分别交AB,CD于点E,F,∠1=47°,则∠2的大小是 .?
12.如图所示,∠1和∠2是直线 , 被第三条直线 所截得的 角.?
13.如图所示,AB∥CD,∠1=50°,∠2=110°,则∠3= .?
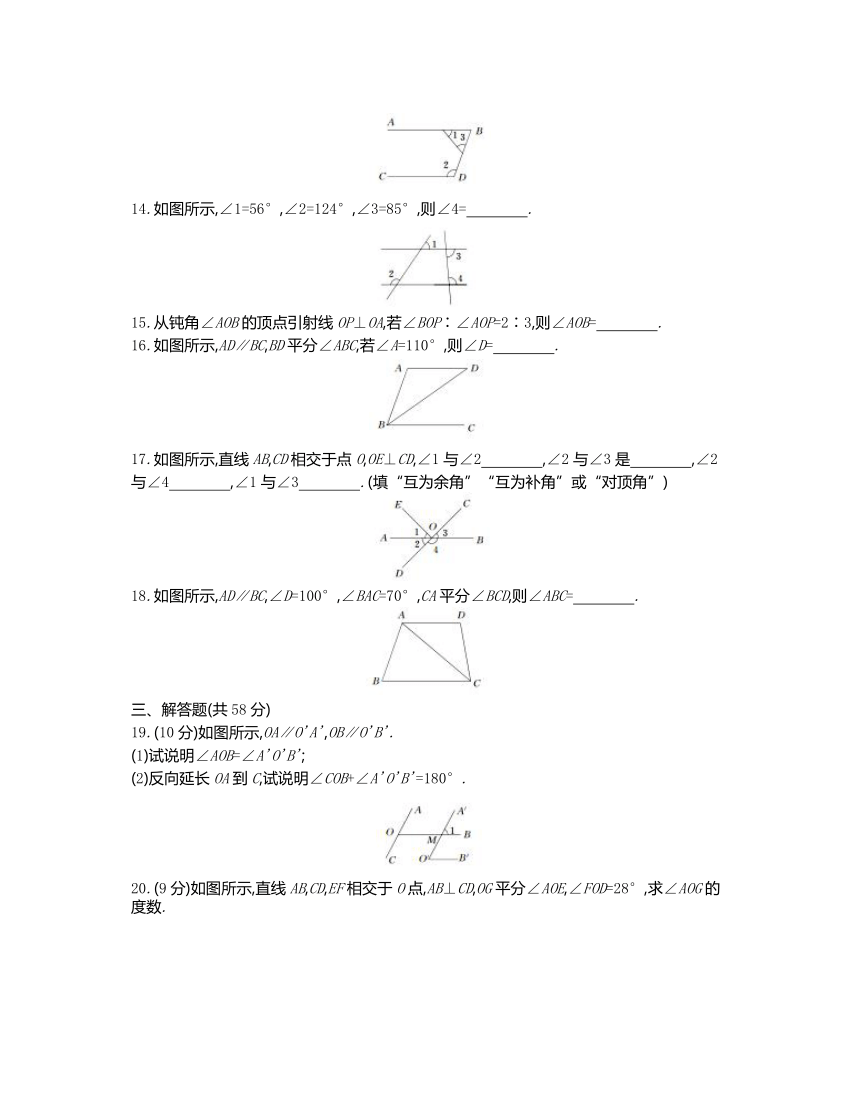
14.如图所示,∠1=56°,∠2=124°,∠3=85°,则∠4= .?
15.从钝角∠AOB的顶点引射线OP⊥OA,若∠BOP∶∠AOP=2∶3,则∠AOB= .?
16.如图所示,AD∥BC,BD平分∠ABC,若∠A=110°,则∠D= .?
17.如图所示,直线AB,CD相交于点O,OE⊥CD,∠1与∠2 ,∠2与∠3是 ,∠2与∠4 ,∠1与∠3 .(填“互为余角”“互为补角”或“对顶角”)?
18.如图所示,AD∥BC,∠D=100°,∠BAC=70°,CA平分∠BCD,则∠ABC= .?
三、解答题(共58分)
19.(10分)如图所示,OA∥O'A',OB∥O'B'.
(1)试说明∠AOB=∠A'O'B';
(2)反向延长OA到C,试说明∠COB+∠A'O'B'=180°.
20.(9分)如图所示,直线AB,CD,EF相交于O点,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠AOG的度数.
21.(9分)如图所示,已知∠1=∠2,∠3=∠4,∠5=∠6.试说明AD∥BC.
22.(9分)按要求作图(不写作法,但要保留作图痕迹).
已知点P,Q分别在∠AOB的边OA,OB上.
①作直线PQ.
②过点P作OB的垂线.
③过点Q作OA的平行线.
23.(9分)如图所示,已知AD⊥BC,EF⊥BC,∠3=∠C,那么∠1=∠2.谈谈你的理由.
24.(12分)已知AB∥CD,试解决下列问题:
(1)如图(1)所示,∠1+∠2等于多少度?请说明理由;
(2)如图(2)所示,∠1+∠2+∠3等于多少度?请说明理由;
(3)如图(3)所示,∠1+∠2+∠3+∠4等于多少度?为什么?
(4)如图(4)所示,试探究∠1+∠2+∠3+∠4+…+∠n等于多少度.
【答案与解析】
1.B(解析:因为∠AEC+∠AED=180°,∠AEC=100°,所以∠AED=80°.因为AB∥DF,所以∠D=∠AED=80°.故选B.)
2.A(解析:A中有不平行的情况.)
3.D(解析:根据平行线的判定即可得到答案.)
4.C(解析:A.平行的传递性.B.平行线的判定.C.同位角相等,两直线才平行.D.平行线的判定.)
5.C(解析:可以举反例说明.)
6.D(解析:根据对顶角相等及平行线的性质可以得出.)
7.B(解析:两直线平行,内错角相等.)
8.C(解析:先求∠END,再求∠FND,∠2=∠FND=60°.)
9.B(解析:①没说两直线平行,②如果这点在该直线上就作不出平行线,④如果三线共点就只有1个交点.)
10.C(解析:两直线平行,同旁内角互补.)
11.133°(解析:因为∠1=∠AEF,∠1=47°,所以∠AEF=47°.因为AB∥CD,所以∠AEF+∠2=180°,所以∠2=180°- ∠AEF=133°.)
12.AC BD AB 同位
13.60°
14.95°(解析:根据∠1+∠2=180°得∠1的对顶角+∠2=180°,进而得到平行线,则∠3+∠4=180°,所以∠4=180°- 85°=95°.)
15.150°(解析:∠AOP=90°,∠BOP=60°.)
16.35°
17.互为余角 对顶角 互为补角 互为余角
18.70°(解析:∠BCD=180°- ∠D=80°,∠ACB=∠BCD=40°,∠DAC=∠ACB=40°,∠BAD=∠DAC+∠BAC=110°,∠ABC=180°- ∠BAD=70°.)
19.解:(1)因为OA∥O'A'(已知),所以∠AOB=∠1(两直线平行,同位角相等).又因为OB∥O'B'(已知),所以∠1=∠A'O'B'(两直线平行,同位角相等),所以∠AOB=∠A'O'B'(等量代换). (2)因为AO∥A'O'(已知),所以∠COB+∠OMO'=180°(两直线平行,同旁内角互补).又因为OB∥O'B'(已知),所以∠OMO'=∠A'O'B'(两直线平行,内错角相等),所以∠COB+∠A'O'B'=180°(等量代换).
20.解:因为AB⊥CD,所以∠AOF=90°- ∠FOD=90°- 28°=62°,所以∠AOE=180°- ∠AOF=118°.因为OG平分∠AOE,所以∠AOG=∠AOE=59°.
21.解:因为∠5=∠6(已知),所以AB∥CE(内错角相等,两直线平行),所以∠4+∠2+∠5=180°(两直线平行,同旁内角互补).因为∠3=∠4,∠1=∠2(已知),所以∠3+∠1+∠5=180°(等量代换),所以AD∥BC(同旁内角互补,两直线平行).
22.解:如图所示.
23.解:因为AD⊥BC(已知),EF⊥BC(已知),所以∠ADC=∠EFC=90°(垂直定义),所以AD∥EF(同位角相等,两直线平行),所以∠1=∠DAC(两直线平行,同位角相等).又因为∠3=∠C(已知),所以AC∥GD(同位角相等,两直线平行),所以∠2=∠DAC(两直线平行,内错角相等),所以∠1=∠2(等量代换).
24.解:(1)因为AB∥CD,所以∠1+∠2=180°(两直线平行,同旁内角互补). (2)如图(1)所示,过点E作EF平行于AB,因为AB∥CD,所以CD∥EF,所以∠1+∠AEF=180°,∠FEC+∠3=180°,所以∠1+∠2+∠3=360°. (3)如图(2)所示,过点E,F分别作EG,FH平行于AB,因为AB∥CD,所以AB∥EG∥FH∥CD,所以∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°,所以∠1+∠2+∠3+∠4=540°. (4)根据上述规律,显然作(n- 2)条辅助线,运用(n- 1)次两条直线平行,同旁内角互补,即可得到∠1+∠2+∠3+∠4+…+∠n=180°(n- 1).
(时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图所示,直线AB,CD相交于点E,DF∥AB.若∠AEC=100°,则∠D等于 ( )
A.70° B.80° C.90° D.100°
2.下列说法不正确的是 ( )
A.若两个相等的角有一组边平行,则另一组边也平行
B.两条直线相交,所成的两组对顶角的平分线互相垂直
C.两条平行线被第三条直线所截,同旁内角的平分线互相垂直
D.经过直线外一点,有且只有一条直线与已知直线平行
3.如图所示,直线a,b都和直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的有 ( )
A.①③ B.②④
C.①③④ D.①②③④
4.下列说法不正确的是 ( )
A.如果两条直线都和第三条直线平行,那么这两条直线也平行
B.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
C.两条直线被第三条直线所截,如果同位角互补,那么这两条直线平行
D.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
5.下列说法中正确的是 ( )
A.相等的两个角是对顶角
B.一条直线有且只有一条垂线
C.直线外一点与这条直线上的各点所连接的线段中,垂线段最短
D.一个角一定不等于它的余角
6.如图所示,直线l1∥l2,∠1=120°,则∠2的度数为 ( )
A.60° B.80° C.100° D.120°
7.如图所示,已知直线a,b被直线c所截,且a∥b,∠1=65°,那么∠2等于 ( )
A.145° B.65° C.55° D.35°
8.如图所示,AB∥CD,EF分别交AB,CD于M,N,NG平分∠DNF,∠1=60°,则∠2等于 ( )
A.40° B.50° C.60° D.70°
9.下列说法中正确的有 ( )
①同位角相等;
②过一点有且只有一条直线与已知直线平行;
③平面内,过一点有且只有一条直线与已知直线垂直;
④三条直线两两相交总有三个交点;
⑤若a∥b,b∥c,则a∥c.
A.1个 B.2个 C.3个 D.4个
10.如图所示,下列推理正确的是 ( )
A.因为∠1=∠4,所以BC∥AD
B.因为∠2=∠3,所以AB∥CD
C.因为AD∥BC,所以∠BCD+∠ADC=180°
D.因为∠1+∠2+∠C=180°,所以BC∥AD
二、填空题(每小题4分,共32分)
11.如图所示,AB∥CD,直线EF分别交AB,CD于点E,F,∠1=47°,则∠2的大小是 .?
12.如图所示,∠1和∠2是直线 , 被第三条直线 所截得的 角.?
13.如图所示,AB∥CD,∠1=50°,∠2=110°,则∠3= .?
14.如图所示,∠1=56°,∠2=124°,∠3=85°,则∠4= .?
15.从钝角∠AOB的顶点引射线OP⊥OA,若∠BOP∶∠AOP=2∶3,则∠AOB= .?
16.如图所示,AD∥BC,BD平分∠ABC,若∠A=110°,则∠D= .?
17.如图所示,直线AB,CD相交于点O,OE⊥CD,∠1与∠2 ,∠2与∠3是 ,∠2与∠4 ,∠1与∠3 .(填“互为余角”“互为补角”或“对顶角”)?
18.如图所示,AD∥BC,∠D=100°,∠BAC=70°,CA平分∠BCD,则∠ABC= .?
三、解答题(共58分)
19.(10分)如图所示,OA∥O'A',OB∥O'B'.
(1)试说明∠AOB=∠A'O'B';
(2)反向延长OA到C,试说明∠COB+∠A'O'B'=180°.
20.(9分)如图所示,直线AB,CD,EF相交于O点,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠AOG的度数.
21.(9分)如图所示,已知∠1=∠2,∠3=∠4,∠5=∠6.试说明AD∥BC.
22.(9分)按要求作图(不写作法,但要保留作图痕迹).
已知点P,Q分别在∠AOB的边OA,OB上.
①作直线PQ.
②过点P作OB的垂线.
③过点Q作OA的平行线.
23.(9分)如图所示,已知AD⊥BC,EF⊥BC,∠3=∠C,那么∠1=∠2.谈谈你的理由.
24.(12分)已知AB∥CD,试解决下列问题:
(1)如图(1)所示,∠1+∠2等于多少度?请说明理由;
(2)如图(2)所示,∠1+∠2+∠3等于多少度?请说明理由;
(3)如图(3)所示,∠1+∠2+∠3+∠4等于多少度?为什么?
(4)如图(4)所示,试探究∠1+∠2+∠3+∠4+…+∠n等于多少度.
【答案与解析】
1.B(解析:因为∠AEC+∠AED=180°,∠AEC=100°,所以∠AED=80°.因为AB∥DF,所以∠D=∠AED=80°.故选B.)
2.A(解析:A中有不平行的情况.)
3.D(解析:根据平行线的判定即可得到答案.)
4.C(解析:A.平行的传递性.B.平行线的判定.C.同位角相等,两直线才平行.D.平行线的判定.)
5.C(解析:可以举反例说明.)
6.D(解析:根据对顶角相等及平行线的性质可以得出.)
7.B(解析:两直线平行,内错角相等.)
8.C(解析:先求∠END,再求∠FND,∠2=∠FND=60°.)
9.B(解析:①没说两直线平行,②如果这点在该直线上就作不出平行线,④如果三线共点就只有1个交点.)
10.C(解析:两直线平行,同旁内角互补.)
11.133°(解析:因为∠1=∠AEF,∠1=47°,所以∠AEF=47°.因为AB∥CD,所以∠AEF+∠2=180°,所以∠2=180°- ∠AEF=133°.)
12.AC BD AB 同位
13.60°
14.95°(解析:根据∠1+∠2=180°得∠1的对顶角+∠2=180°,进而得到平行线,则∠3+∠4=180°,所以∠4=180°- 85°=95°.)
15.150°(解析:∠AOP=90°,∠BOP=60°.)
16.35°
17.互为余角 对顶角 互为补角 互为余角
18.70°(解析:∠BCD=180°- ∠D=80°,∠ACB=∠BCD=40°,∠DAC=∠ACB=40°,∠BAD=∠DAC+∠BAC=110°,∠ABC=180°- ∠BAD=70°.)
19.解:(1)因为OA∥O'A'(已知),所以∠AOB=∠1(两直线平行,同位角相等).又因为OB∥O'B'(已知),所以∠1=∠A'O'B'(两直线平行,同位角相等),所以∠AOB=∠A'O'B'(等量代换). (2)因为AO∥A'O'(已知),所以∠COB+∠OMO'=180°(两直线平行,同旁内角互补).又因为OB∥O'B'(已知),所以∠OMO'=∠A'O'B'(两直线平行,内错角相等),所以∠COB+∠A'O'B'=180°(等量代换).
20.解:因为AB⊥CD,所以∠AOF=90°- ∠FOD=90°- 28°=62°,所以∠AOE=180°- ∠AOF=118°.因为OG平分∠AOE,所以∠AOG=∠AOE=59°.
21.解:因为∠5=∠6(已知),所以AB∥CE(内错角相等,两直线平行),所以∠4+∠2+∠5=180°(两直线平行,同旁内角互补).因为∠3=∠4,∠1=∠2(已知),所以∠3+∠1+∠5=180°(等量代换),所以AD∥BC(同旁内角互补,两直线平行).
22.解:如图所示.
23.解:因为AD⊥BC(已知),EF⊥BC(已知),所以∠ADC=∠EFC=90°(垂直定义),所以AD∥EF(同位角相等,两直线平行),所以∠1=∠DAC(两直线平行,同位角相等).又因为∠3=∠C(已知),所以AC∥GD(同位角相等,两直线平行),所以∠2=∠DAC(两直线平行,内错角相等),所以∠1=∠2(等量代换).
24.解:(1)因为AB∥CD,所以∠1+∠2=180°(两直线平行,同旁内角互补). (2)如图(1)所示,过点E作EF平行于AB,因为AB∥CD,所以CD∥EF,所以∠1+∠AEF=180°,∠FEC+∠3=180°,所以∠1+∠2+∠3=360°. (3)如图(2)所示,过点E,F分别作EG,FH平行于AB,因为AB∥CD,所以AB∥EG∥FH∥CD,所以∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°,所以∠1+∠2+∠3+∠4=540°. (4)根据上述规律,显然作(n- 2)条辅助线,运用(n- 1)次两条直线平行,同旁内角互补,即可得到∠1+∠2+∠3+∠4+…+∠n=180°(n- 1).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
