人教版2019学年初中数学八年级下《17.1 勾股定理》同步练习题(含答案)
文档属性
| 名称 | 人教版2019学年初中数学八年级下《17.1 勾股定理》同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-28 22:08:21 | ||
图片预览

文档简介
人教版2019学年初中数学8年级下《17.1 勾股定理》同步练习题
评卷人 得 分
一.选择题(共10小题)
1.如图,△ABC中,AB=AC,AB=5,BC=8,AD是∠BAC的平分线,则AD的长为( )
A.5 B.4 C.3 D.2
2.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=7,且AC+BC=8,则AB的长为( )
A.6 B.2 C.5 D.
3.在△ABC中,∠C=90°,c2=2b2,则两直角边a,b的关系是( )
A.a<b B.a>b
C.a=b D.以上三种情况都有可能
4.已知直角三角形的两条边长分别是3和5,那么这个三角形的第三条边的长为( )
A.4 B.16 C. D.4或
5.直角三角形有一条直角边长为3,另外两条边长是连续自然数,则周长为( )
A.12 B.18 C.10 D.9
6.下列各组数中,能作为直角三角形三边长的是( )
A.4,5,6 B.5,7,12 C.3,5, D.1,,
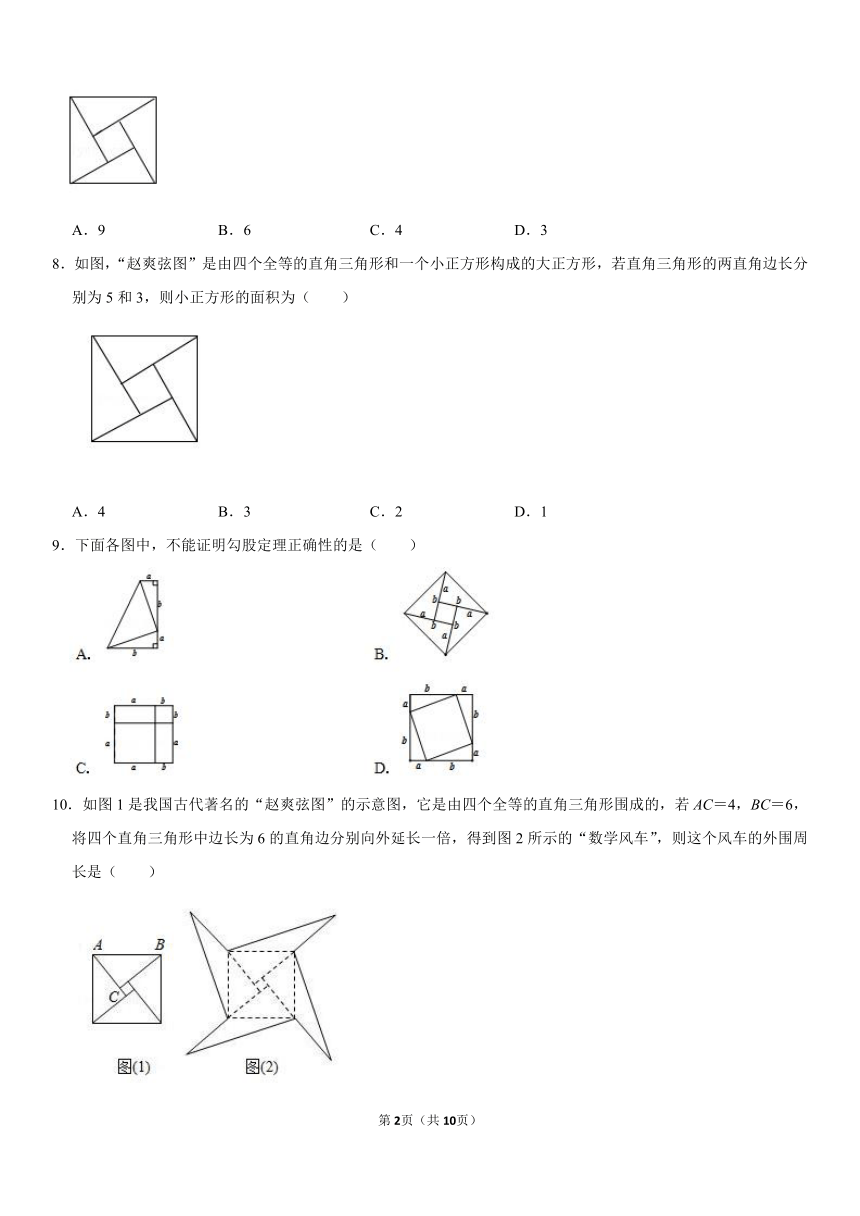
7.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
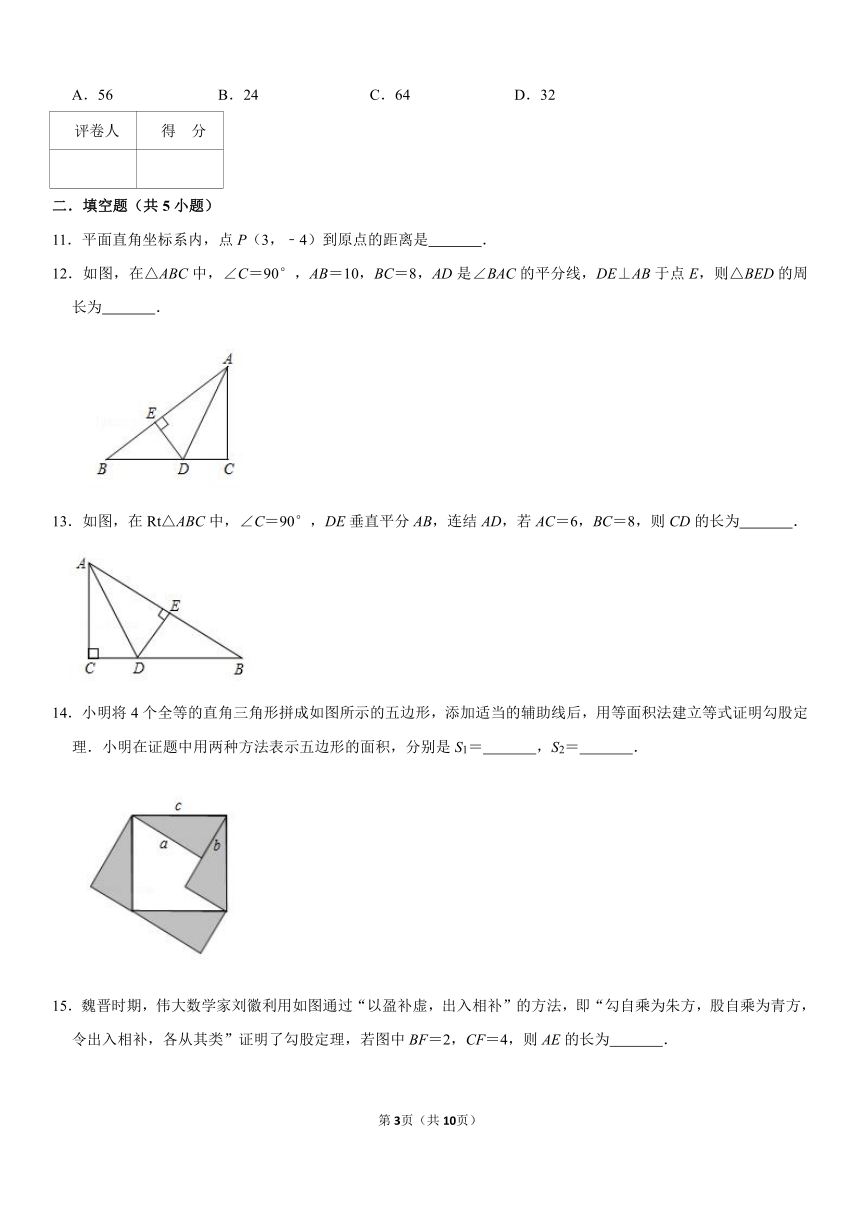
8.如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若直角三角形的两直角边长分别为5和3,则小正方形的面积为( )
A.4 B.3 C.2 D.1
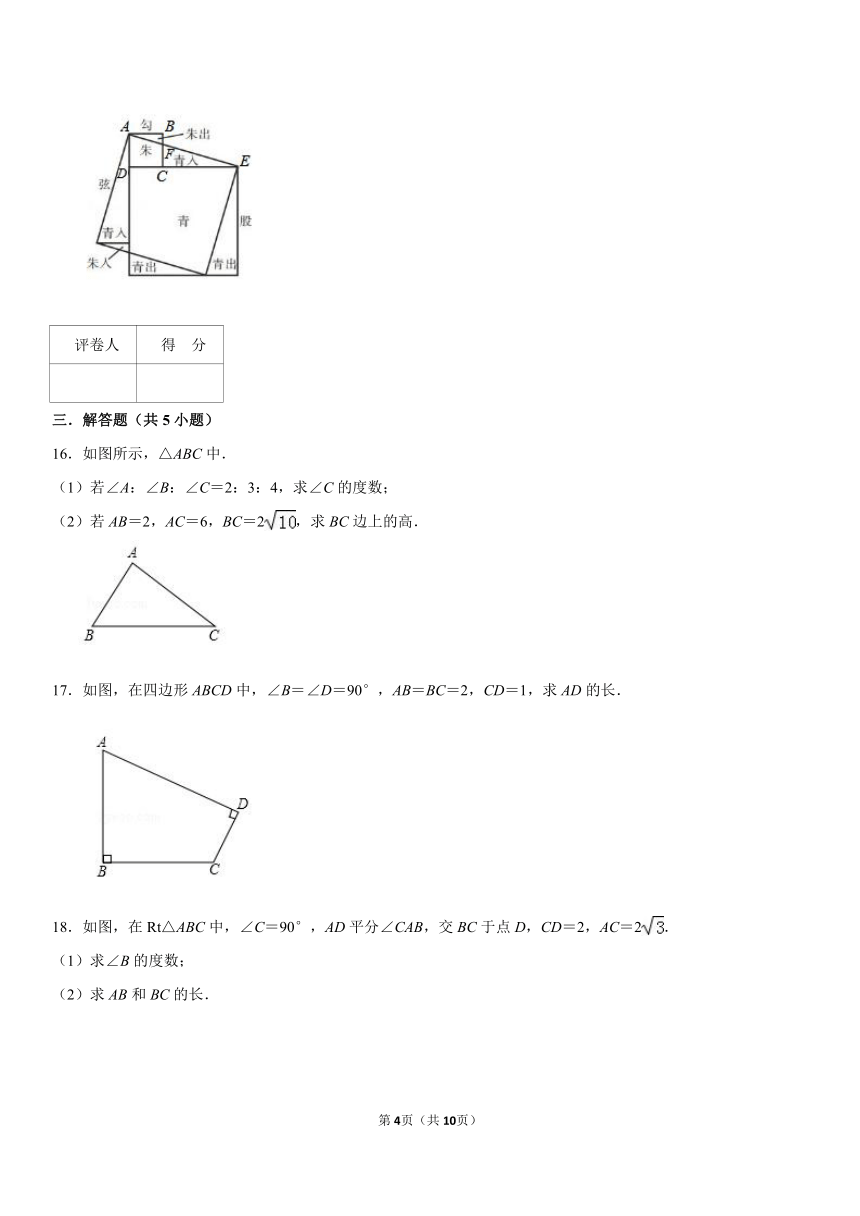
9.下面各图中,不能证明勾股定理正确性的是( )
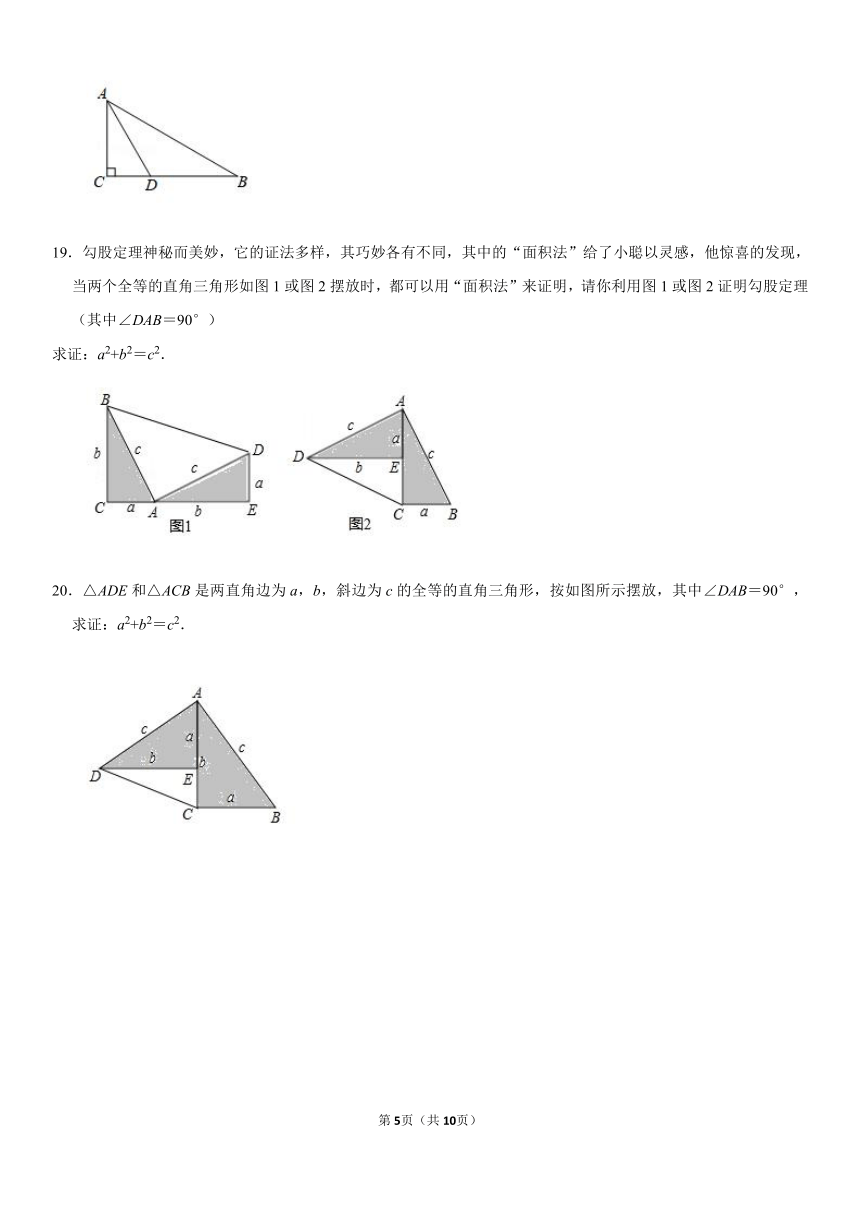
10.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=4,BC=6,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A.56 B.24 C.64 D.32
评卷人 得 分
二.填空题(共5小题)
11.平面直角坐标系内,点P(3,﹣4)到原点的距离是 .
12.如图,在△ABC中,∠C=90°,AB=10,BC=8,AD是∠BAC的平分线,DE⊥AB于点E,则△BED的周长为 .
13.如图,在Rt△ABC中,∠C=90°,DE垂直平分AB,连结AD,若AC=6,BC=8,则CD的长为 .
14.小明将4个全等的直角三角形拼成如图所示的五边形,添加适当的辅助线后,用等面积法建立等式证明勾股定理.小明在证题中用两种方法表示五边形的面积,分别是S1= ,S2= .
15.魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为 .
评卷人 得 分
三.解答题(共5小题)
16.如图所示,△ABC中.
(1)若∠A:∠B:∠C=2:3:4,求∠C的度数;
(2)若AB=2,AC=6,BC=2,求BC边上的高.
17.如图,在四边形ABCD中,∠B=∠D=90°,AB=BC=2,CD=1,求AD的长.
18.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=2,AC=2.
(1)求∠B的度数;
(2)求AB和BC的长.
19.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,请你利用图1或图2证明勾股定理(其中∠DAB=90°)
求证:a2+b2=c2.
20.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
人教版2019学年初中数学8年级下《17.1 勾股定理》同步练习题
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:∵AB=AC,AD是∠BAC的平分线,
∴BD=BC=4,AD⊥BC,
由勾股定理得,AD==3,
故选:C.
2.【解答】解:由勾股定理得,AC2+BC2=AB2,
∵S1+S2=7,
∴×π×()2+×π×()2+×AC×BC﹣×π×()2=7,
∴AC×BC=14,
AB===6,
故选:A.
3.【解答】解:∵在Rt△ABC中,∠C=90°,
∴a2+b2=c2,
∵c2=2b2,
∴a2+b2=2b2,
∴a=b,
故选:C.
4.【解答】解:当3和5都是直角边时,第三边长为:=;
当5是斜边长时,第三边长为:=4.
故选:D.
5.【解答】解:设直角三角形的另一条直角边为x,则斜边长为x+1,
由勾股定理得,x2+32=(x+1)2,
解得,x=4,
∴直角三角形的另一条直角边为4,则斜边长为5,
∴周长=3+4+5=12,
故选:A.
6.【解答】解:A、∵52+42≠62,∴三条线段不能组成直角三角形,故A选项错误;
B、∵52+72≠122,∴三条线段不能组成直角三角形,故B选项错误;
C、∵32+()2≠52,∴三条线段不能组成直角三角形,故C选项错误;
D、∵12+()2=()2,∴三条线段能组成直角三角形,故D选项正确;
故选:D.
7.【解答】解:由题意可知:中间小正方形的边长为:a﹣b,
∵每一个直角三角形的面积为:ab=×8=4,
∴4×ab+(a﹣b)2=25,
∴(a﹣b)2=25﹣16=9,
∴a﹣b=3,
故选:D.
8.【解答】解:3和5为两条直角边长时,
小正方形的边长=5﹣3=2,
∴小正方形的面积22=4;
故选:A.
9.【解答】解:A、∵+c2+ab=(a+b)(a+b),
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
B、∵4×+(b﹣a)2=c2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
C、根据图形不能证明勾股定理,故本选项符合题意;
D、∵4×+c2=(a+b)2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
故选:C.
10.【解答】解:依题意,设“数学风车”中的四个直角三角形的斜边长为x,则
x2=82+62=100
所以x=10
所以“数学风车”的周长是:(10+4)×4=56.
故选:A.
二.填空题(共5小题)
11.【解答】解:P(3,﹣4)到原点的距离==5,
故答案为:5.
12.【解答】解:∵∠C=90°,AB=10,BC=8,
∴由勾股定理可得,Rt△ABC中,AC=6,
∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,AD=AD,
∴△ADE≌△ADC(AAS),
∴CD=ED,AE=AC=6,
又∵AB=10,
∴BE=4,
∴△BED的周长=BD+CD+BE=BD+CD+BE=BC+BE=8+4=12,
故答案为:12.
13.【解答】解:∵DE是AB的中垂线,
∴DA=DB,
设AD=x,则DB=x,CD=BC﹣BD=8﹣x,
在Rt△ACD中,∵AC2+CD2=AD2,
∴62+(8﹣x)2=x2,
解得x=,
∴CD=8﹣x=,
故答案为:.
14.【解答】解:如图所示:
S1=c2+ab×2=c2+ab,
S2=a2+b2+ab×2=a2+b2+ab.
故答案为:c2+ab,a2+b2+ab.
15.【解答】解:∵BF=2,CF=4,
∴BC=BF+CF=2+4=6,
∵AB∥EC,
∴=,即=,
解得:CE=12,
在Rt△ADE中,AD=6,DE=DC+CE=6+12=18,
根据勾股定理得:AE==6,
故答案为:6.
三.解答题(共5小题)
16.【解答】解:设∠A=2k,∠B=3k,∠C=4k,
由题意得,2k+3k+4k=180°,
解得k=20°,
所以,∠C=4×20°=80°,
(2)∵AB=2,AC=6,BC=2,
∴BC2=AB2+AC2,
∴△ABC是直角三角形,
∴BC边上的高=.
17.【解答】解:连接AC,
∵∠B=90°
∴AC2=AB2+BC2.
∵AB=BC=2
∴AC2=8.
∵∠D=90°
∴AD2=AC2﹣CD2.
∵CD=1,
∴AD2=7.
∴.
18.【解答】解:(1)∵在Rt△ACD中,∠C=90°,CD=2,AC=2,
∴tan∠CAD===,
∴∠CAD=30°,
∵AD平分∠CAB,
∴∠CAB=2∠CAD=60°,
∵∠C=90°,
∴∠B=90°﹣60°=30°;
(2)∵在Rt△ABC中,∠C=90°,∠B=30°,
∴AB=2AC=4,
∴BC==6.
19.【解答】解:利用图1进行证明:
证明:∵∠DAB=90°,点C,A,E在一条直线上,BC∥DE,则CE=a+b,
∵S四边形BCED=S△ABC+S△ABD+S△AED=ab+c2+ab,
又∵S四边形BCED=(a+b)2,
∴ab+c2+ab=(a+b)2,
∴a2+b2=c2.
利用图2进行证明:
证明:如图,连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,∵S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a),
∴b2+ab=c2+a(b﹣a),
∴a2+b2=c2.
20.【解答】证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a.
∵S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)
∴a2+b2=c2
第10页(共10页)
