高中数学第二章推理与证明2.3.1数学归纳法课件 新人教B版选修2_2(37张)
文档属性
| 名称 | 高中数学第二章推理与证明2.3.1数学归纳法课件 新人教B版选修2_2(37张) |

|
|
| 格式 | zip | ||
| 文件大小 | 937.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-01 00:00:00 | ||
图片预览











文档简介
课件37张PPT。数学归纳法请问:?以上三个结论正确吗?为什么?
?得出以上结论所用的方法有什么共同点和什么不同点 问题 1:今天,据观察第一个到学校的是男同学,第二个到学校的也是男同学,第三个到学校的还是男同学,于是得出:这所学校里的学生都是男同学。 问题 3:教师根据成绩单,逐一核实后下结论:“全班及格” 问题 2:三角形的内角和为180o,四边形的内角和为2?180o,五边形的内 角和为3?180o,于是有:凸n边形的内角和为(n-2) ?180o。
? 共同点:均用了归纳法得出结论;不同点:问题1、2是用的不完全 归纳法,问题3是用的完全归纳法。一、提出问题? 1、错2、对3、对二、概念1、归纳法定义:
对于某类事物,由它的一些特殊事例或其全部可能情况,归纳出一般结论的推理方法,叫归纳法。2、归纳法分类:
归纳法 想一想:由两种归纳法得出的结论一定正确吗?说 明:(1)不完全归纳法有利于发现问题,但结论
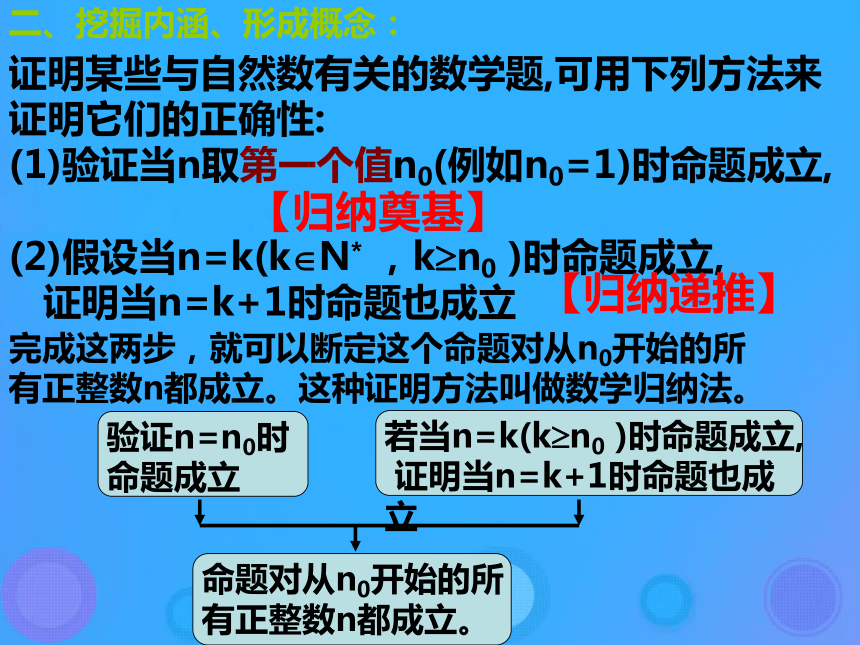
不一定正确。(2)完全归纳法结论可靠,但一一核对困难。提出问题如何寻找一种严格推理的归纳法?思考?有若干块骨牌竖直摆放,若将它们全部推倒,有什么办法?一般地,多米诺骨牌游戏的原理是什么?(条件是什么)创设情境⑴ 第一块骨牌倒下;⑵ 任意相邻的两块骨牌,前一块倒下一定导致后一块倒下?两个条件的作用:条件⑴:奠基;条件⑵:递推关系二、挖掘内涵、形成概念:证明某些与自然数有关的数学题,可用下列方法来证明它们的正确性:
(1)验证当n取第一个值n0(例如n0=1)时命题成立,
(2)假设当n=k(k?N* ,k?n0 )时命题成立,
证明当n=k+1时命题也成立完成这两步,就可以断定这个命题对从n0开始的所有正整数n都成立。这种证明方法叫做数学归纳法。【归纳奠基】【归纳递推】例题:用数学归纳法证明(二)、数学归纳法的步骤根据(1)(2)知对任意的 时命题成立。注:(1)证明当 取第一个值 或 时结论正确两个步骤缺一不可:仅靠第一步不能说明结论的普遍性;仅有第二步没有第一步,就失去了递推的依据。只有把第一、二步的结论结合在一起才能得出普遍性结论。因此完成一二两步后,还要做一个总的结论。(3)数学归纳法用来证明与正整数有关的命题。(1)(2)用数学归纳法证明:
练习1用数学归纳法证明:
证明:
请你来批作业第二步的证明没有用上归纳假设!用数学归纳法证明:
证明:
练习1
证明:1、当n=1时,左=12=1,右=
∴n=1时,等式成立
2、假设n=k时,等式成立,即
那么,当n=k+1时
左=12+22+…+k2+(k+1)2=
=右
∴n=k+1时,原等式成立
由1、2知当n?N*时,原等式都成立练习1.用数学归纳法证明第二步的证明要用上归纳假设!(1)在第二步中,证明n=k+1命题成立时,必须用到
n=k命题成立这一归纳假设,否则就打破数学
归纳法步骤之间的逻辑严密关系,造成推理无
效. 证明中的几个注意问题:(2)在第一步中的初始值不一定从1取起,证明时
应根据具体情况而定.(3)在证明n=k+1命题成立用到n=k命题成立时,要
分析命题的结构特点,分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别.弄清
应增加的项.1)明确首先取值n0并验证命题真假(必不可少);
2)“假设n=k时命题正确”并写出命题形式;
3)分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别,弄清左端应增加的项;
4)明确等式左端变形目标,掌握恒等式变形常用的方法:乘法公式、因式分解、添拆项、配方等;
5)两个步骤、一个结论缺一不可,否则结论不能成立:
递推基础不可少,归纳假设要用到,结论写明莫忘掉用数学归纳法证明恒等式的步骤及注意事项:多米诺骨牌动画演示返回问题情境三 题型一 用数学归纳法证明等式问题第二步的证明要用上归纳假设!例3、已知正数数列{an}中,前n项和为sn,且
用数学归纳法证明:证:(1)当n=1时,
=1,结论成立.(2)假设当n=k时,结论成立,即则当n=k+1时,故当n=k+1时,结论也成立.根据(1)、(2)知,对一切正整数n,结论都成立.第二步的证明要用上归纳假设!题型二 用数学归纳法证明不等式问题例5、用数学归纳法证明:证:(1)当n=2时, 左边= 不等式
成立.(2)假设当n=k(k≥2)时不等式成立,即有: 则当n=k+1时,我们有:题型二 用数学归纳法证明不等式问题即当n=k+1时,不等式也成立.由(1)、(2)原不等式对一切 都成立. 例6、证明不等式:证:(1)当n=1时,左边=1,右边=2, 不等式显然成立.(2)假设当n=k时不等式成立,即有:则当n=k+1时,我们有:即当n=k+1时,不等式也成立.根据(1)、(2)可知,原不等式对一切正整数都 成立.例7、求证:证:(1)当n=2时,左边= ,右边= ,由于
故不等式成立. (2)假设n=k( )时命题成立,即
则当n=k+1时,
即当n=k+1时,命题成立.由(1)、(2)原不等式对一切 都成立. 例8、已知x> ?1,且x?0,n?N,n?2.
求证:(1+x)n>1+nx.(2)假设n=k时,不等式成立,即 (1+x)k>1+kx
当n=k+1时,因为x> ?1 ,所以1+x>0,于是
左边=(1+x)k+1=(1+x)k(1+x)>(1+x)(1+kx)=1+(k+1)x+kx2;
右边=1+(k+1)x.
因为kx2>0,所以左边>右边,即(1+x)k+1>1+(k+1)x.
这就是说,原不等式当n=k+1时也成立.
根据(1)和(2),原不等式对任何不小于2的自然数n都成立.证明: (1)当n=2时,左=(1+x)2=1+2x+x2
∵ x?0,∴ 1+2x+x2>1+2x=右
∴n=1时不等式成立例9、已知 求证 : . 证:(1)当n=2时, ,
不等式成立.(2)假设当n=k(k≥2)时不等式成立,即则当n=k+1时, 有:即当n=k+1时,不等式成立.由(1),(2)所证不等式对一切 都成立. 题型三 用数学归纳法证明整除问题例11、用数学归纳法证明:
当n为正偶数时,xn-yn能被x+y整除.证:(1)当n=2时,x2-y2=(x+y)(x-y),即能被x+y整除,故命
题成立.(2)假设当n=2k时,命题成立,即x2k-y2k能被x+y整除.则当n=2k+2时,有 都能被x+y整除.故x2k+2-y2k+2能被x+y整除,即当n=2k+2时命题成立.由(1)、(2)知原命题对一切正偶数均成立.例12、用数学归纳法证明: 能被8
整除.证:(1)当n=1时,A1=5+2+1=8,命题显然成立.(2)假设当n=k时,Ak能被8整除,即
是8的倍数.那么:因为Ak是8的倍数,3k-1+1是偶数即4(3k-1+1)也是
8的倍数,所以Ak+1也是8的倍数,即当n=k+1时,命题成立.由(1)、(2)知对一切正整数n, An能被8整除.例13、求证:x3n-1+x3n-2+1能被x2+x+1整除.证:(1)当n=1时, x3n-1+x3n-2+1= x2+x+1,从而命题成立.(2)假设当n=k时命题成立,即x3k-1+x3k-2+1能被
x2+x+1整除则当n=k+1时,x3(k+1)-1+x3(k+12+1=x3k+2+x3k+1+1=x3(x3k-1+x3k-2+1)-x3+1
= x3(x3k-1+x3k-2+1)-(x-1)(x2+x+1)因为x3k-1+x3k-2+1、x2+x+1都能被x2+x+1)-整除,所以上式右边能被x2+x+1整除.即当n=k+1时,命题成立.根据(1)、(2)知,对一切正整数n,命题成立.题型四 用数学归纳法证明几何问题例15、平面内有n (n?2)条直线,任何两条都不平行,任何三条不过同一点,问交点的 个数 为多少?并证明.当n=k+1时:第k+1条直线分别与前k条直线各交于
一点,共增加k个点,由1)、2)可知,对一切n∈N?原命题均成立。证明:1)n=2时:两条直线交点个数为1,
而f(2)= ×2×(2-1)=1, ∴命题成立。 ∴k+1条直线交点个数=f(k)+k= k(k-1)+k
= k(k-1+2)= k(k+1)= (k+1)[(k+1)-1]=f(k+1),
即当n=k+1时命题仍成立。2)假设n=k(k∈N?,k≥2)时,k条直线交点个数为
f(k)= k(k-1),题型四 用数学归纳法证明几何问题题型五 用数学归纳法解决探究性问题题型五 用数学归纳法解决探究性问题例18、是否存在常数a、b,使得等式:
对一切正整数n都成立,并证明你的结论.解:令n=1,2,并整理得以下用数学归纳法证明:
(1)当n=1时,由上面解法知结论正确.题型五 用数学归纳法解决探究性问题(2)假设当n=k时结论正确,即:
则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.
?得出以上结论所用的方法有什么共同点和什么不同点 问题 1:今天,据观察第一个到学校的是男同学,第二个到学校的也是男同学,第三个到学校的还是男同学,于是得出:这所学校里的学生都是男同学。 问题 3:教师根据成绩单,逐一核实后下结论:“全班及格” 问题 2:三角形的内角和为180o,四边形的内角和为2?180o,五边形的内 角和为3?180o,于是有:凸n边形的内角和为(n-2) ?180o。
? 共同点:均用了归纳法得出结论;不同点:问题1、2是用的不完全 归纳法,问题3是用的完全归纳法。一、提出问题? 1、错2、对3、对二、概念1、归纳法定义:
对于某类事物,由它的一些特殊事例或其全部可能情况,归纳出一般结论的推理方法,叫归纳法。2、归纳法分类:
归纳法 想一想:由两种归纳法得出的结论一定正确吗?说 明:(1)不完全归纳法有利于发现问题,但结论
不一定正确。(2)完全归纳法结论可靠,但一一核对困难。提出问题如何寻找一种严格推理的归纳法?思考?有若干块骨牌竖直摆放,若将它们全部推倒,有什么办法?一般地,多米诺骨牌游戏的原理是什么?(条件是什么)创设情境⑴ 第一块骨牌倒下;⑵ 任意相邻的两块骨牌,前一块倒下一定导致后一块倒下?两个条件的作用:条件⑴:奠基;条件⑵:递推关系二、挖掘内涵、形成概念:证明某些与自然数有关的数学题,可用下列方法来证明它们的正确性:
(1)验证当n取第一个值n0(例如n0=1)时命题成立,
(2)假设当n=k(k?N* ,k?n0 )时命题成立,
证明当n=k+1时命题也成立完成这两步,就可以断定这个命题对从n0开始的所有正整数n都成立。这种证明方法叫做数学归纳法。【归纳奠基】【归纳递推】例题:用数学归纳法证明(二)、数学归纳法的步骤根据(1)(2)知对任意的 时命题成立。注:(1)证明当 取第一个值 或 时结论正确两个步骤缺一不可:仅靠第一步不能说明结论的普遍性;仅有第二步没有第一步,就失去了递推的依据。只有把第一、二步的结论结合在一起才能得出普遍性结论。因此完成一二两步后,还要做一个总的结论。(3)数学归纳法用来证明与正整数有关的命题。(1)(2)用数学归纳法证明:
练习1用数学归纳法证明:
证明:
请你来批作业第二步的证明没有用上归纳假设!用数学归纳法证明:
证明:
练习1
证明:1、当n=1时,左=12=1,右=
∴n=1时,等式成立
2、假设n=k时,等式成立,即
那么,当n=k+1时
左=12+22+…+k2+(k+1)2=
=右
∴n=k+1时,原等式成立
由1、2知当n?N*时,原等式都成立练习1.用数学归纳法证明第二步的证明要用上归纳假设!(1)在第二步中,证明n=k+1命题成立时,必须用到
n=k命题成立这一归纳假设,否则就打破数学
归纳法步骤之间的逻辑严密关系,造成推理无
效. 证明中的几个注意问题:(2)在第一步中的初始值不一定从1取起,证明时
应根据具体情况而定.(3)在证明n=k+1命题成立用到n=k命题成立时,要
分析命题的结构特点,分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别.弄清
应增加的项.1)明确首先取值n0并验证命题真假(必不可少);
2)“假设n=k时命题正确”并写出命题形式;
3)分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别,弄清左端应增加的项;
4)明确等式左端变形目标,掌握恒等式变形常用的方法:乘法公式、因式分解、添拆项、配方等;
5)两个步骤、一个结论缺一不可,否则结论不能成立:
递推基础不可少,归纳假设要用到,结论写明莫忘掉用数学归纳法证明恒等式的步骤及注意事项:多米诺骨牌动画演示返回问题情境三 题型一 用数学归纳法证明等式问题第二步的证明要用上归纳假设!例3、已知正数数列{an}中,前n项和为sn,且
用数学归纳法证明:证:(1)当n=1时,
=1,结论成立.(2)假设当n=k时,结论成立,即则当n=k+1时,故当n=k+1时,结论也成立.根据(1)、(2)知,对一切正整数n,结论都成立.第二步的证明要用上归纳假设!题型二 用数学归纳法证明不等式问题例5、用数学归纳法证明:证:(1)当n=2时, 左边= 不等式
成立.(2)假设当n=k(k≥2)时不等式成立,即有: 则当n=k+1时,我们有:题型二 用数学归纳法证明不等式问题即当n=k+1时,不等式也成立.由(1)、(2)原不等式对一切 都成立. 例6、证明不等式:证:(1)当n=1时,左边=1,右边=2, 不等式显然成立.(2)假设当n=k时不等式成立,即有:则当n=k+1时,我们有:即当n=k+1时,不等式也成立.根据(1)、(2)可知,原不等式对一切正整数都 成立.例7、求证:证:(1)当n=2时,左边= ,右边= ,由于
故不等式成立. (2)假设n=k( )时命题成立,即
则当n=k+1时,
即当n=k+1时,命题成立.由(1)、(2)原不等式对一切 都成立. 例8、已知x> ?1,且x?0,n?N,n?2.
求证:(1+x)n>1+nx.(2)假设n=k时,不等式成立,即 (1+x)k>1+kx
当n=k+1时,因为x> ?1 ,所以1+x>0,于是
左边=(1+x)k+1=(1+x)k(1+x)>(1+x)(1+kx)=1+(k+1)x+kx2;
右边=1+(k+1)x.
因为kx2>0,所以左边>右边,即(1+x)k+1>1+(k+1)x.
这就是说,原不等式当n=k+1时也成立.
根据(1)和(2),原不等式对任何不小于2的自然数n都成立.证明: (1)当n=2时,左=(1+x)2=1+2x+x2
∵ x?0,∴ 1+2x+x2>1+2x=右
∴n=1时不等式成立例9、已知 求证 : . 证:(1)当n=2时, ,
不等式成立.(2)假设当n=k(k≥2)时不等式成立,即则当n=k+1时, 有:即当n=k+1时,不等式成立.由(1),(2)所证不等式对一切 都成立. 题型三 用数学归纳法证明整除问题例11、用数学归纳法证明:
当n为正偶数时,xn-yn能被x+y整除.证:(1)当n=2时,x2-y2=(x+y)(x-y),即能被x+y整除,故命
题成立.(2)假设当n=2k时,命题成立,即x2k-y2k能被x+y整除.则当n=2k+2时,有 都能被x+y整除.故x2k+2-y2k+2能被x+y整除,即当n=2k+2时命题成立.由(1)、(2)知原命题对一切正偶数均成立.例12、用数学归纳法证明: 能被8
整除.证:(1)当n=1时,A1=5+2+1=8,命题显然成立.(2)假设当n=k时,Ak能被8整除,即
是8的倍数.那么:因为Ak是8的倍数,3k-1+1是偶数即4(3k-1+1)也是
8的倍数,所以Ak+1也是8的倍数,即当n=k+1时,命题成立.由(1)、(2)知对一切正整数n, An能被8整除.例13、求证:x3n-1+x3n-2+1能被x2+x+1整除.证:(1)当n=1时, x3n-1+x3n-2+1= x2+x+1,从而命题成立.(2)假设当n=k时命题成立,即x3k-1+x3k-2+1能被
x2+x+1整除则当n=k+1时,x3(k+1)-1+x3(k+12+1=x3k+2+x3k+1+1=x3(x3k-1+x3k-2+1)-x3+1
= x3(x3k-1+x3k-2+1)-(x-1)(x2+x+1)因为x3k-1+x3k-2+1、x2+x+1都能被x2+x+1)-整除,所以上式右边能被x2+x+1整除.即当n=k+1时,命题成立.根据(1)、(2)知,对一切正整数n,命题成立.题型四 用数学归纳法证明几何问题例15、平面内有n (n?2)条直线,任何两条都不平行,任何三条不过同一点,问交点的 个数 为多少?并证明.当n=k+1时:第k+1条直线分别与前k条直线各交于
一点,共增加k个点,由1)、2)可知,对一切n∈N?原命题均成立。证明:1)n=2时:两条直线交点个数为1,
而f(2)= ×2×(2-1)=1, ∴命题成立。 ∴k+1条直线交点个数=f(k)+k= k(k-1)+k
= k(k-1+2)= k(k+1)= (k+1)[(k+1)-1]=f(k+1),
即当n=k+1时命题仍成立。2)假设n=k(k∈N?,k≥2)时,k条直线交点个数为
f(k)= k(k-1),题型四 用数学归纳法证明几何问题题型五 用数学归纳法解决探究性问题题型五 用数学归纳法解决探究性问题例18、是否存在常数a、b,使得等式:
对一切正整数n都成立,并证明你的结论.解:令n=1,2,并整理得以下用数学归纳法证明:
(1)当n=1时,由上面解法知结论正确.题型五 用数学归纳法解决探究性问题(2)假设当n=k时结论正确,即:
则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.
