高中数学第二章推理与证明2.1.1合情推理课件 新人教B版选修2_2(35张)
文档属性
| 名称 | 高中数学第二章推理与证明2.1.1合情推理课件 新人教B版选修2_2(35张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-01 00:00:00 | ||
图片预览










文档简介
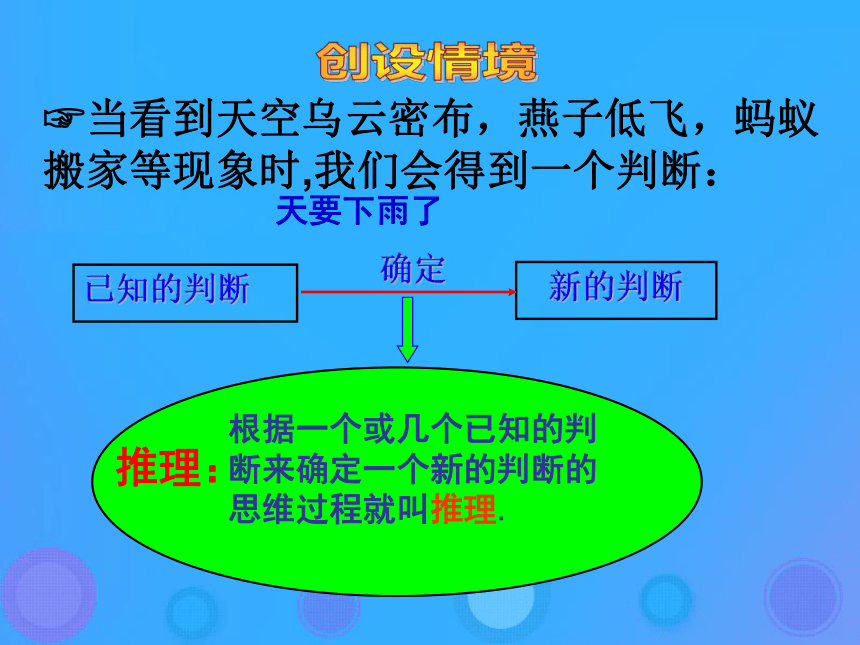
课件35张PPT。——归纳推理与类比推理合情推理(第一课时)?当看到天空乌云密布,燕子低飞,蚂蚁搬家等现象时,我们会得到一个判断:推理: 创设情境天要下雨了根据一个或几个已知的判断来确定一个新的判断的思维过程就叫推理.已知的判断新的判断确定数学来源于生活,离不开生活,离不开观察和推理。【探究】: 例1、已知数列 的第一项 且 ,
试猜想出这个数列的通项公式。例2、由铜、铁、铝、金、银等金属都能导电,
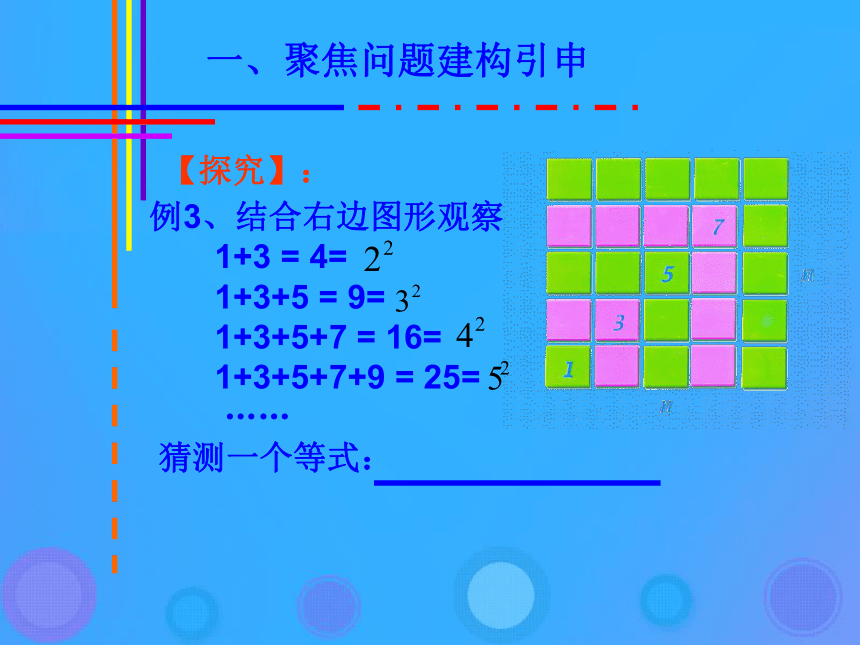
猜想:一、聚焦问题建构引申【探究】: 一、聚焦问题建构引申例3、结合右边图形观察
1+3 = 4=
1+3+5 = 9=
1+3+5+7 = 16=
1+3+5+7+9 = 25=
……
猜测一个等式: 二、抽象思维形成概念【分组讨论】: 1、以上推理的特点是什么?2、(一)归纳推理:由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理(简称归纳).
特点:部分到整体 个别到一般【活动一】:感受归纳推理的魅力请同学展示歌德巴赫猜想过程 6=3+3
8=3+5
10=3+7
12=5+7
14=7+7
……
40= + 猜想:
“任何一个不小于6的偶数都等于两个奇质数之和”二、抽象思维形成概念陈氏定理除了归纳在人们的创造发明活动中,还常常应用类比。我国古代工匠鲁班,类比带齿的草叶,发明了锯。苍蝇的眼睛是一种“复眼”,由3000多只小眼组成,人们模仿它制成了“蝇眼透镜”,一次就能照出千百张相同的照片。人们仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.可能有生命存在(猜想)有生命存在(事实)温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否存在生命?(二)类比推理:由两类对象具有某些类似特征和其中的一类对象的某些特征,推出另一类对象也具有这些特征的推理,称为类比推理(简称类比).
特点:特殊到特殊 空间向量的性质例4、利用平面向量的性质类比得空间向量平面向量我们把前面所进行的推理过程概括为:从具体问题出发观察、分析、比较、联想归纳、类比提出猜想可见,归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理。三、实践应用训练升华【活动二】:我们一起来推理 练习1、观察下面等式, 并得出一般结论:归纳推理可以提供解决问题的思路和方向三、实践应用训练升华【活动二】:我们一起来推理练习2、数一数图中的凸多面体的面数F、顶点
数V和棱数E,填表并探求它们之间的关系. 三、实践应用训练升华【活动二】:我们一起来推理足球有12块黑皮子,20块白皮子,黑皮是五边形,白皮是六边形,有60个顶点,猜想:足球有多少条棱? 练习3、类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想:三、实践应用训练升华【活动二】:我们一起来推理类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想:三、实践应用训练升华【活动二】:我们一起来推理练习4、定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列 是等和数列,且 ,公和为5 ,求 的值和这个数列的前n项和 的计算公式。类比推理可以提供解决问题的思路和方向四、趣味再尝试1、观察图形规律,在其右下角的空格处的图形为( ) A、 B、 C、 D、
2、将所有的自然数按如图规律排列:
2 3 6 7 10 11 0 1 4 5 8 9
则从2017到2019的顺序为( ), A、 B、 C、 D、 通俗地说,合情推理是指“合乎情理”的推理。一般来说合情推理得到的结论,仅仅是一种猜测,未必可靠。费马数费马通过对下列式子的观察、分析观察、分析猜想——验证——再猜想 合情推理的结果需要检验证明五、与高考链接合情推理是每年高考的常考内容,主要形式有:
1、与数字有关的推理
2、与不等式有关的推理
3、与图形有关的推理
4、与实际问题有关的推理
五、与高考链接2、已知 ,观察下列各式 : ,
...... ,类比得则 五、与高考链接4、与实际问题有关的推理
(2016 · 全国高考卷II)有三张卡片,分别写有1和2,1和3,2和3。甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 类比推理由特殊到特殊的推理;以旧的知识为基础,推测新的结果;结论不一定成立.归纳推理由部分到整体、特殊到一般的推理;以观察分析为基础,推测新的结论;具有发现的功能;结论不一定成立.具有发现的功能;六、开放思考总结反思在数学研究中:(2)证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向。(1)得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论;六、开放思考总结反思【总结】:我的收获七、反馈评价拓展延伸
2、找一个你感兴趣的数学定义、公式或定理,探究它的来源,你也可以通过翻阅书籍、上网查找资料来寻求依据。推荐:歌尼斯堡七桥问题四色猜想谢谢!合情推理游戏:河内塔(Tower of Hanoi) 传说在古老的印度有一座神庙,神庙中有三根针和套在一根针上的64个圆环。古印度的天神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
23如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了。
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次?123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =2时, =3 =1时, =1 =3时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则归纳可得用递推公式 通俗地说,合情推理是指“合乎情理”的推理。一般来说合情推理得到的结论,仅仅是一种猜测,未必可靠。
试猜想出这个数列的通项公式。例2、由铜、铁、铝、金、银等金属都能导电,
猜想:一、聚焦问题建构引申【探究】: 一、聚焦问题建构引申例3、结合右边图形观察
1+3 = 4=
1+3+5 = 9=
1+3+5+7 = 16=
1+3+5+7+9 = 25=
……
猜测一个等式: 二、抽象思维形成概念【分组讨论】: 1、以上推理的特点是什么?2、(一)归纳推理:由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理(简称归纳).
特点:部分到整体 个别到一般【活动一】:感受归纳推理的魅力请同学展示歌德巴赫猜想过程 6=3+3
8=3+5
10=3+7
12=5+7
14=7+7
……
40= + 猜想:
“任何一个不小于6的偶数都等于两个奇质数之和”二、抽象思维形成概念陈氏定理除了归纳在人们的创造发明活动中,还常常应用类比。我国古代工匠鲁班,类比带齿的草叶,发明了锯。苍蝇的眼睛是一种“复眼”,由3000多只小眼组成,人们模仿它制成了“蝇眼透镜”,一次就能照出千百张相同的照片。人们仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.可能有生命存在(猜想)有生命存在(事实)温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否存在生命?(二)类比推理:由两类对象具有某些类似特征和其中的一类对象的某些特征,推出另一类对象也具有这些特征的推理,称为类比推理(简称类比).
特点:特殊到特殊 空间向量的性质例4、利用平面向量的性质类比得空间向量平面向量我们把前面所进行的推理过程概括为:从具体问题出发观察、分析、比较、联想归纳、类比提出猜想可见,归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理。三、实践应用训练升华【活动二】:我们一起来推理 练习1、观察下面等式, 并得出一般结论:归纳推理可以提供解决问题的思路和方向三、实践应用训练升华【活动二】:我们一起来推理练习2、数一数图中的凸多面体的面数F、顶点
数V和棱数E,填表并探求它们之间的关系. 三、实践应用训练升华【活动二】:我们一起来推理足球有12块黑皮子,20块白皮子,黑皮是五边形,白皮是六边形,有60个顶点,猜想:足球有多少条棱? 练习3、类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想:三、实践应用训练升华【活动二】:我们一起来推理类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想:三、实践应用训练升华【活动二】:我们一起来推理练习4、定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列 是等和数列,且 ,公和为5 ,求 的值和这个数列的前n项和 的计算公式。类比推理可以提供解决问题的思路和方向四、趣味再尝试1、观察图形规律,在其右下角的空格处的图形为( ) A、 B、 C、 D、
2、将所有的自然数按如图规律排列:
2 3 6 7 10 11 0 1 4 5 8 9
则从2017到2019的顺序为( ), A、 B、 C、 D、 通俗地说,合情推理是指“合乎情理”的推理。一般来说合情推理得到的结论,仅仅是一种猜测,未必可靠。费马数费马通过对下列式子的观察、分析观察、分析猜想——验证——再猜想 合情推理的结果需要检验证明五、与高考链接合情推理是每年高考的常考内容,主要形式有:
1、与数字有关的推理
2、与不等式有关的推理
3、与图形有关的推理
4、与实际问题有关的推理
五、与高考链接2、已知 ,观察下列各式 : ,
...... ,类比得则 五、与高考链接4、与实际问题有关的推理
(2016 · 全国高考卷II)有三张卡片,分别写有1和2,1和3,2和3。甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 类比推理由特殊到特殊的推理;以旧的知识为基础,推测新的结果;结论不一定成立.归纳推理由部分到整体、特殊到一般的推理;以观察分析为基础,推测新的结论;具有发现的功能;结论不一定成立.具有发现的功能;六、开放思考总结反思在数学研究中:(2)证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向。(1)得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论;六、开放思考总结反思【总结】:我的收获七、反馈评价拓展延伸
2、找一个你感兴趣的数学定义、公式或定理,探究它的来源,你也可以通过翻阅书籍、上网查找资料来寻求依据。推荐:歌尼斯堡七桥问题四色猜想谢谢!合情推理游戏:河内塔(Tower of Hanoi) 传说在古老的印度有一座神庙,神庙中有三根针和套在一根针上的64个圆环。古印度的天神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
23如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了。
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次?123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =2时, =3 =1时, =1 =3时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则归纳可得用递推公式 通俗地说,合情推理是指“合乎情理”的推理。一般来说合情推理得到的结论,仅仅是一种猜测,未必可靠。
