高中数学第一章导数及其应用1.3.1利用导数判断函数的单调性课件 新人教B版选修2_2(20张)
文档属性
| 名称 | 高中数学第一章导数及其应用1.3.1利用导数判断函数的单调性课件 新人教B版选修2_2(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 436.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-01 21:22:08 | ||
图片预览








文档简介
课件20张PPT。利用导数判断函数的单调性(4)对数函数的导数:(5)指数函数的导数: (3).三角函数 : (1)常函数:(C)/ ? 0, (c为常数); (2)幂函数 : (xn)/ ? nxn?1
1.基本初等函数的导数公式 2.导数的运算法则(1)函数的和或差的导数 (u±v)/=u/±v/.
(3)函数的商的导数
( ) / = (v≠0)。
(2)函数的积的导数(uv)/=u/v+v/u
函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时1)都有 f ( x 1 ) < f ( x 2 ),则 f ( x ) 在G 上是增函数;2)都有 f ( x 1 ) > f ( x 2 ),则 f ( x ) 在G 上是减函数;若 f(x) 在G上是增函数或减函数,则 f(x) 在G上具有严格的单调性。G 称为单调区间复习:例 : 已知函数y=2x3-6x2+7,求证:这个函
数在区间(0,2)上是单调递增的.
(1)任取x1 ( 2 ) 作差f(x1)-f(x2)并变形
(3)判断符号
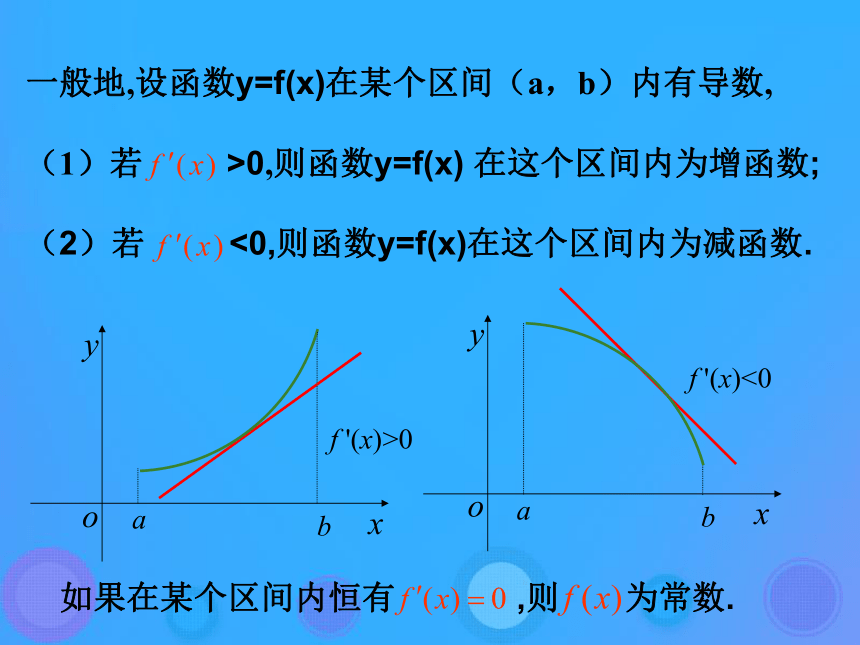
(4)下结论用定义法判断函数单调性的步骤:观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系. f '(x)>0f '(x)<0一般地,设函数y=f(x)在某个区间(a,b)内有导数,
(1)若 >0,则函数y=f(x) 在这个区间内为增函数;
(2)若 <0,则函数y=f(x)在这个区间内为减函数.如果在某个区间内恒有 ,则 为常数.例1 .确定函数f(x)=2x3-6x2+7在哪个区间
内是增函数,哪个区间内是减函数.解:f′(x)=(2x3-6x2+7)′=6x2-12x解f′(x)= 6x2-12x>0,
得x>2或x<0∴f(x)的增函数区间为 (-∞,0) ,(2,+∞) .解f′(x)= 6x2-12x<0,解得0<x<2.
∴f(x)的减函数区间为(0,2).例1.确定函数f(x)=2x3-6x2+7在哪个区间
内是增函数,哪个区间内是减函数. 用导数法确定函数的单调性时的步骤是:
(1)求出函数的导函数(注意定义域)
(2)求解不等式 > 0, < 0,
(3)指出函数的单调区间上的单调性注:单调区间不以“并集”出现。 导数的应用:判断单调性、求单调区间练习1:求下列函数 的单调区间.函数的增函数区间为
减函数区间为函数的增函数区间为
减函数区间为(2)f(x)=x-lnx注意:要确定函数的定义 域.
练习3:确定下列函数的单调区间:
(1)f(x)=x-sinx;∴y=x+ 的单调减区间是(-1,0)和(0,1)例4已知函数y=x+ ,试讨论出此函数的单调区间.解:y′=(x+ )′=1-1·x-2
=令 >0. 解得x>1或x<-1.∴y=x+ 的单调增区间是(-∞,-1)
和(1,+∞).令 <0,解得-1<x<0或0<x<1.3.3.1例6:设f(x)=ax3+x恰有三个单调区间,试确定a的取值
范 围,并求其单调区间.解:若a>0, 对一切实数恒成立,此时f(x)只有一
个单调区间,矛盾.若a=0, 此时f(x)也只有一个单调区间,矛盾. 若a<0,则 ,易知此时f(x)
恰有三个单调区间.故a<0,其单调区间是:单调递增区间:单调递减区间: 和证明:令f(x)=e2x-1-2x. ∴f′(x)=2e2x-2=2(e2x-1)
∵x>0,∴e2x>e0=1,∴2(e2x-1)>0, 即f′(x)>0
∴f(x)=e2x-1-2x在(0,+∞)上是增函数.
∵f(0)=e0-1-0=0.
∴当x>0时,f(x)>f(0)=0,即e2x-1-2x>0.
∴1+2x<e2x例4当x>0时,证明不等式:1+2x<e2x.分析:假设令f(x)=e2x-1-2x.∵f(0)=e0-1-0=0, 如果能够证明f(x)在(0,+∞)上是增函数,那么f(x)>0,则不等式就可以证明.点评:所以以后要证明不等式时,可以利用函数的单调性进行证明,把特殊点找出来使函数的值为0. 例6(2000年全国高考题)设函数其中a>0,求a的取值范围,使函数f(x)在区间 上是单调函数。即1、函数的减区间为( )
(A) (-1,1) (B) (1,2)
(C) (-∞,-1) (D) (-∞,-1) ,(1, +∞) 2、若函数y=a(x3-x)的递减区间为( ),
则a的取值范围为( )
(A) a>0 (B) –11 (D) 0单调递增函数
单调递减函数
(C) 部份单调增,部分单调减
(D) 单调性不能确定 课堂练习
1.基本初等函数的导数公式 2.导数的运算法则(1)函数的和或差的导数 (u±v)/=u/±v/.
(3)函数的商的导数
( ) / = (v≠0)。
(2)函数的积的导数(uv)/=u/v+v/u
函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时1)都有 f ( x 1 ) < f ( x 2 ),则 f ( x ) 在G 上是增函数;2)都有 f ( x 1 ) > f ( x 2 ),则 f ( x ) 在G 上是减函数;若 f(x) 在G上是增函数或减函数,则 f(x) 在G上具有严格的单调性。G 称为单调区间复习:例 : 已知函数y=2x3-6x2+7,求证:这个函
数在区间(0,2)上是单调递增的.
(1)任取x1
(3)判断符号
(4)下结论用定义法判断函数单调性的步骤:观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系. f '(x)>0f '(x)<0一般地,设函数y=f(x)在某个区间(a,b)内有导数,
(1)若 >0,则函数y=f(x) 在这个区间内为增函数;
(2)若 <0,则函数y=f(x)在这个区间内为减函数.如果在某个区间内恒有 ,则 为常数.例1 .确定函数f(x)=2x3-6x2+7在哪个区间
内是增函数,哪个区间内是减函数.解:f′(x)=(2x3-6x2+7)′=6x2-12x解f′(x)= 6x2-12x>0,
得x>2或x<0∴f(x)的增函数区间为 (-∞,0) ,(2,+∞) .解f′(x)= 6x2-12x<0,解得0<x<2.
∴f(x)的减函数区间为(0,2).例1.确定函数f(x)=2x3-6x2+7在哪个区间
内是增函数,哪个区间内是减函数. 用导数法确定函数的单调性时的步骤是:
(1)求出函数的导函数(注意定义域)
(2)求解不等式 > 0, < 0,
(3)指出函数的单调区间上的单调性注:单调区间不以“并集”出现。 导数的应用:判断单调性、求单调区间练习1:求下列函数 的单调区间.函数的增函数区间为
减函数区间为函数的增函数区间为
减函数区间为(2)f(x)=x-lnx注意:要确定函数的定义 域.
练习3:确定下列函数的单调区间:
(1)f(x)=x-sinx;∴y=x+ 的单调减区间是(-1,0)和(0,1)例4已知函数y=x+ ,试讨论出此函数的单调区间.解:y′=(x+ )′=1-1·x-2
=令 >0. 解得x>1或x<-1.∴y=x+ 的单调增区间是(-∞,-1)
和(1,+∞).令 <0,解得-1<x<0或0<x<1.3.3.1例6:设f(x)=ax3+x恰有三个单调区间,试确定a的取值
范 围,并求其单调区间.解:若a>0, 对一切实数恒成立,此时f(x)只有一
个单调区间,矛盾.若a=0, 此时f(x)也只有一个单调区间,矛盾. 若a<0,则 ,易知此时f(x)
恰有三个单调区间.故a<0,其单调区间是:单调递增区间:单调递减区间: 和证明:令f(x)=e2x-1-2x. ∴f′(x)=2e2x-2=2(e2x-1)
∵x>0,∴e2x>e0=1,∴2(e2x-1)>0, 即f′(x)>0
∴f(x)=e2x-1-2x在(0,+∞)上是增函数.
∵f(0)=e0-1-0=0.
∴当x>0时,f(x)>f(0)=0,即e2x-1-2x>0.
∴1+2x<e2x例4当x>0时,证明不等式:1+2x<e2x.分析:假设令f(x)=e2x-1-2x.∵f(0)=e0-1-0=0, 如果能够证明f(x)在(0,+∞)上是增函数,那么f(x)>0,则不等式就可以证明.点评:所以以后要证明不等式时,可以利用函数的单调性进行证明,把特殊点找出来使函数的值为0. 例6(2000年全国高考题)设函数其中a>0,求a的取值范围,使函数f(x)在区间 上是单调函数。即1、函数的减区间为( )
(A) (-1,1) (B) (1,2)
(C) (-∞,-1) (D) (-∞,-1) ,(1, +∞) 2、若函数y=a(x3-x)的递减区间为( ),
则a的取值范围为( )
(A) a>0 (B) –1
单调递减函数
(C) 部份单调增,部分单调减
(D) 单调性不能确定 课堂练习
