三年级下册数学课件 总复习 解决问题和混合运算 青岛版(五年制) (共28张PPT)
文档属性
| 名称 | 三年级下册数学课件 总复习 解决问题和混合运算 青岛版(五年制) (共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-01 22:13:17 | ||
图片预览







文档简介
青岛版小学数学三年级下册
——解决问题和混合运算
——解决问题和混合运算
温故知新(二)
诊断:
(200-20)÷10
找错了总价,总价应该是付的钱减去找回的20元。
总价÷数量=单价
单价×数量=总价
总价÷单价=数量
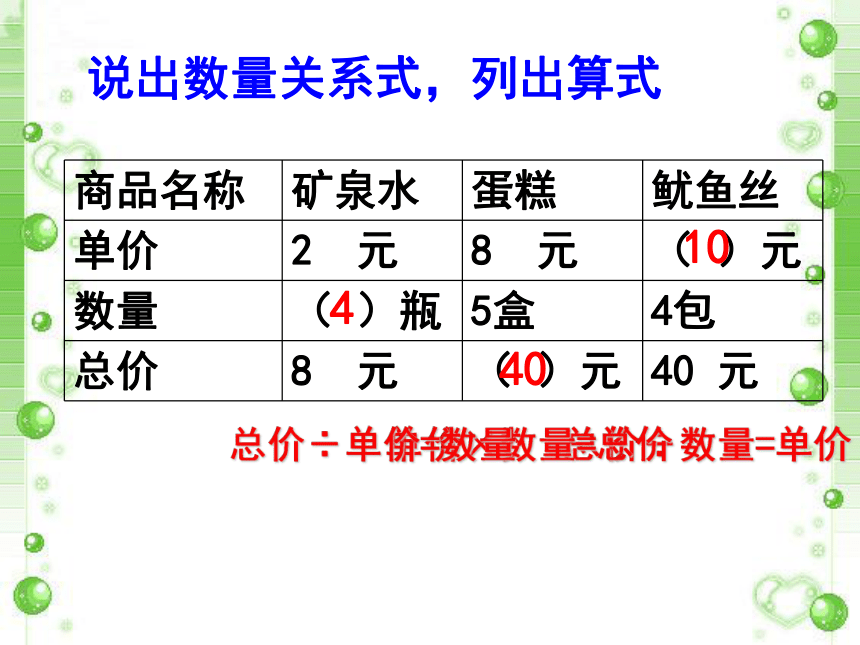
说出数量关系式,列出算式
4
40
10
总价÷数量=单价
单价×数量=总价
总价÷单价=数量
商品名称 矿泉水 蛋糕 鱿鱼丝
单价 2 元 8 元 ( )元
数量 ( )瓶 5盒 4包
总价 8 元 ( )元 40 元
分析问题
数量关系
思考过程:
确定思路
速度×时间=路程
路程÷时间=速度
路程÷速度=时间
小华家离学校的路程是630米,步行的速度是70米/分,
她7:50出发,8:00能到达学校吗?
比较时间:630÷70=9(分),7:50~8:00有10分钟,10分>9分,所以小华能在8:00到达学校。
比较路程:70×10=700(米),700米>630米,小华能在8:00到达学校。
比较速度:630÷10=63(分),70米/分>63米/分,所以小华能在8:00到达学校。
小华家离学校的路程是630米,步行的速度是70米/分,
她7:50出发,8:00能到达学校吗?
速度×时间=路程
路程÷时间=速度
路程÷速度=时间
单价×数量=总价
总价÷单价=数量
总价÷数量=单价
速度、时间、路程
单价、数量、总价
数量关系
诊断
(24-1)×8
间隔数找错了
间隔数+1=棵数
植树问题
两端都栽:
一端不栽:
两端都不栽:
三种情况
间隔数+1=棵数
间隔数=棵数
间隔数-1=棵数
两端都栽:
一端不栽:
两端都不栽:
一一对应
间隔数+1=棵数
间隔数=棵数
间隔数-1=棵数
一条小路长45米,小路一侧有一排椅子,起点和终点不放椅子,
每两把椅子之间相距9米,一共摆了多少把椅子?
两端都不栽:间隔数-1=棵数
45÷9-1
每小时65千米
每小时75千米
4小时相遇
?千米
甲城
乙城
小货车和大货车分别从甲乙两城同时出发,相向而行,经过4小时相遇,小货车每小时行驶65千米,大货车每小时行驶75千米。
甲乙两城相距多少千米?
65+75
65+75
65+75
65+75
(65+75)×4
?千米
甲城
乙城
速度和×时间=总路程
小货车和大货车分别从甲乙两城同时出发,相向而行,经过4小时相遇,小货车每小时65千米,大货车每小时75千米。东西两城相距多少千米?
4小时
4小时
65 × 4
75 ×4
+
?千米
甲城
乙城
速度1 ×时间+ 速度2 ×时间=总路程
小货车和大货车分别从甲乙两城同时出发,相向而行,经过4小时相遇,小货车每小时65千米,大货车每小时75千米。东西两城相距多少千米?
不带括号的
带括号的
混合运算
例如:
混合运算(没有括号的)
480 ÷ 60 + 55 × 2
= 118
= 8 + 110
在既有乘除又有加减的混合运算中,要先算乘除,再算加减。
在有括号的混合运算中,要先算括号里面,再算括号外面的。既有小括号又有中括号的,要先算小括号里面的,再算中括号里面的。
混合运算(有括号的)
例如:
180 ÷[(76-28)÷ 4]
= 180 ÷[48 ÷ 4]
= 15
= 180 ÷ 12
仔细观察,做出判断。说说错在哪里?
17-7×25÷25
= 10×25÷25
= 250÷25
= 10
×
( )
[15+(24-18)]×20
= 15+6 ×20
= 15+120
= 135
×
( )
仔细观察,做出判断。说说错在哪里?
学校买来200枝钢笔和150个文具盒,一共花去3100元。已知每枝钢笔8元,每个文具盒多少元?
(3100-8×200)÷150
=(3100-1600)÷ 150
= 10(元)
答:每个文具盒10元。
两辆汽车同时从甲乙两地出发相向而行, 一辆车每小时行65千米, 另一辆车每小时行70千米.3小时后两车仍相距55千米,甲乙两地相距多少千米?
甲
乙
每小时65千米
每小时70千米
55千米
?千米
(65+70) ×3 + 55
1.25×4÷25×4 400-400÷25×4
[650-(320+40) ÷ 9] ×2
2. 甲乙两辆汽车同时从A、B两个车站同时出发相向而行,经过5小时在途中相遇,甲车每小时行45千米,乙车每小时行50千米, A、B两站相距多少千米?(用两种方法解答)
3. 一根木头长3米,把它锯成5段,每锯一次的时间是3分钟,据完5段后共用多长时间?
4.学校要买25个篮球,超市原来一个篮球56元,促销活动现降价6元。学校买篮球一共花了多少钱?
全课回顾
课前回顾
唤醒知识
记忆
课上交流
综合练习
构建知识
网络
解决生活
问题
单元反思
错题本
纠错
整理
——解决问题和混合运算
——解决问题和混合运算
温故知新(二)
诊断:
(200-20)÷10
找错了总价,总价应该是付的钱减去找回的20元。
总价÷数量=单价
单价×数量=总价
总价÷单价=数量
说出数量关系式,列出算式
4
40
10
总价÷数量=单价
单价×数量=总价
总价÷单价=数量
商品名称 矿泉水 蛋糕 鱿鱼丝
单价 2 元 8 元 ( )元
数量 ( )瓶 5盒 4包
总价 8 元 ( )元 40 元
分析问题
数量关系
思考过程:
确定思路
速度×时间=路程
路程÷时间=速度
路程÷速度=时间
小华家离学校的路程是630米,步行的速度是70米/分,
她7:50出发,8:00能到达学校吗?
比较时间:630÷70=9(分),7:50~8:00有10分钟,10分>9分,所以小华能在8:00到达学校。
比较路程:70×10=700(米),700米>630米,小华能在8:00到达学校。
比较速度:630÷10=63(分),70米/分>63米/分,所以小华能在8:00到达学校。
小华家离学校的路程是630米,步行的速度是70米/分,
她7:50出发,8:00能到达学校吗?
速度×时间=路程
路程÷时间=速度
路程÷速度=时间
单价×数量=总价
总价÷单价=数量
总价÷数量=单价
速度、时间、路程
单价、数量、总价
数量关系
诊断
(24-1)×8
间隔数找错了
间隔数+1=棵数
植树问题
两端都栽:
一端不栽:
两端都不栽:
三种情况
间隔数+1=棵数
间隔数=棵数
间隔数-1=棵数
两端都栽:
一端不栽:
两端都不栽:
一一对应
间隔数+1=棵数
间隔数=棵数
间隔数-1=棵数
一条小路长45米,小路一侧有一排椅子,起点和终点不放椅子,
每两把椅子之间相距9米,一共摆了多少把椅子?
两端都不栽:间隔数-1=棵数
45÷9-1
每小时65千米
每小时75千米
4小时相遇
?千米
甲城
乙城
小货车和大货车分别从甲乙两城同时出发,相向而行,经过4小时相遇,小货车每小时行驶65千米,大货车每小时行驶75千米。
甲乙两城相距多少千米?
65+75
65+75
65+75
65+75
(65+75)×4
?千米
甲城
乙城
速度和×时间=总路程
小货车和大货车分别从甲乙两城同时出发,相向而行,经过4小时相遇,小货车每小时65千米,大货车每小时75千米。东西两城相距多少千米?
4小时
4小时
65 × 4
75 ×4
+
?千米
甲城
乙城
速度1 ×时间+ 速度2 ×时间=总路程
小货车和大货车分别从甲乙两城同时出发,相向而行,经过4小时相遇,小货车每小时65千米,大货车每小时75千米。东西两城相距多少千米?
不带括号的
带括号的
混合运算
例如:
混合运算(没有括号的)
480 ÷ 60 + 55 × 2
= 118
= 8 + 110
在既有乘除又有加减的混合运算中,要先算乘除,再算加减。
在有括号的混合运算中,要先算括号里面,再算括号外面的。既有小括号又有中括号的,要先算小括号里面的,再算中括号里面的。
混合运算(有括号的)
例如:
180 ÷[(76-28)÷ 4]
= 180 ÷[48 ÷ 4]
= 15
= 180 ÷ 12
仔细观察,做出判断。说说错在哪里?
17-7×25÷25
= 10×25÷25
= 250÷25
= 10
×
( )
[15+(24-18)]×20
= 15+6 ×20
= 15+120
= 135
×
( )
仔细观察,做出判断。说说错在哪里?
学校买来200枝钢笔和150个文具盒,一共花去3100元。已知每枝钢笔8元,每个文具盒多少元?
(3100-8×200)÷150
=(3100-1600)÷ 150
= 10(元)
答:每个文具盒10元。
两辆汽车同时从甲乙两地出发相向而行, 一辆车每小时行65千米, 另一辆车每小时行70千米.3小时后两车仍相距55千米,甲乙两地相距多少千米?
甲
乙
每小时65千米
每小时70千米
55千米
?千米
(65+70) ×3 + 55
1.25×4÷25×4 400-400÷25×4
[650-(320+40) ÷ 9] ×2
2. 甲乙两辆汽车同时从A、B两个车站同时出发相向而行,经过5小时在途中相遇,甲车每小时行45千米,乙车每小时行50千米, A、B两站相距多少千米?(用两种方法解答)
3. 一根木头长3米,把它锯成5段,每锯一次的时间是3分钟,据完5段后共用多长时间?
4.学校要买25个篮球,超市原来一个篮球56元,促销活动现降价6元。学校买篮球一共花了多少钱?
全课回顾
课前回顾
唤醒知识
记忆
课上交流
综合练习
构建知识
网络
解决生活
问题
单元反思
错题本
纠错
整理
同课章节目录
