2018年高中数学第二章推理与证明2.3.1数学归纳法课件 新人教B版选修2_2(25张PPT)
文档属性
| 名称 | 2018年高中数学第二章推理与证明2.3.1数学归纳法课件 新人教B版选修2_2(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 766.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-02 00:00:00 | ||
图片预览








文档简介
课件25张PPT。2.3 数学归纳法思 考 对于数列 ,已知 ,
求通项公式.
猜想:
学 习 目 标1.了解数学归纳的原理2.能用数学归纳法证明一些简单的数学命题
(多米诺骨牌游戏)
思考:此游戏中,能使所有多米诺骨牌全部倒下的条件?1.第一块骨牌倒下2.任意相邻的两块骨牌,
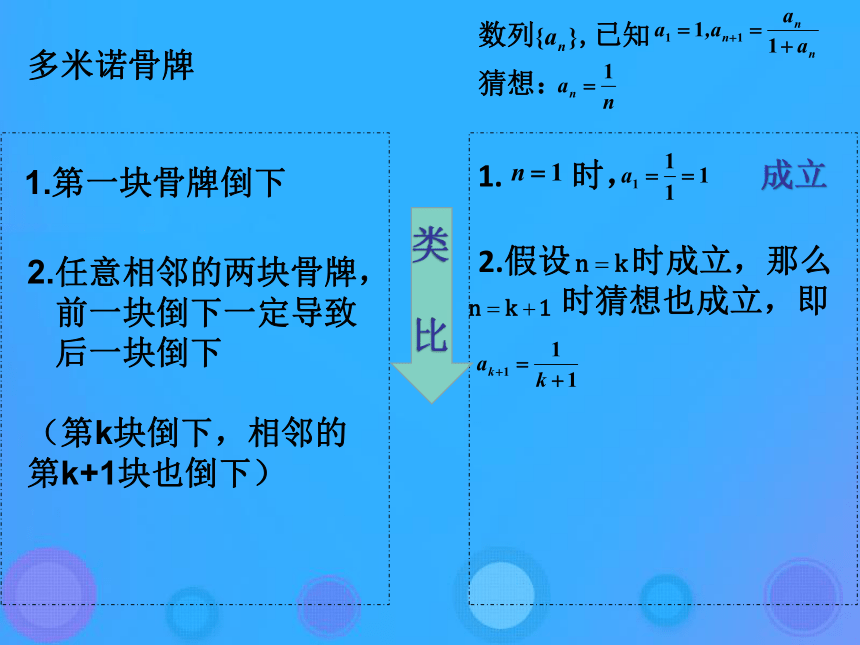
前一块倒下一定导致后一块倒下递推关系:第k块倒下,相邻的第k+1块也倒下情境引入
1.第一块骨牌倒下2.任意相邻的两块骨牌,
前一块倒下一定导致
后一块倒下
(第k块倒下,相邻的第k+1块也倒下)数列 ,已知
猜想:1. 时,成立2.假设 时成立,那么
时猜想也成立,即
多米诺骨牌一般地证明一个与正整数 1.(归纳奠基)证明当 2.(归纳递推)假设当 有关的命题,可按下列步骤进行:取第一个值 时命题成立;时命题成立,
时命题也成立.
证明当数学归纳法证明:(1)当 左边 所以等式成立.(2)假设当 那么,当 即当 根据(1)和(2),可知等式对任何 时,时等式成立,即时等式也成立.都成立.
数学归纳法
变式练习1 用数学归纳法证明 证明(1)当n=1时,左边=1,右边=1,等式成立.这就是说,当n=k+1时,等式也成立.由(1)和(2),可知等式对任何正整数n都成立.(2)假设当n=k时,等式成立,即递推基础递推依据那么当n=k+1时, 分析下列各题用数学归纳法证明过程中的错误:变式训练2纠错!(1)2+4+6+8+…+2n=n2+n+1(n?N*)证明 :假设当n=k时等式成立,即
2+4+6+8+…+2k=k2+k+1(k?N*)那么,当n=k+1时,有
2+4+6+8+…+2k+2(k+1)
=k2+k+1+2(k+1)
=(k+1)2+(k+1)+1 ,
因此,对于任何n?N*等式都成立。缺乏“递推基础”事实上,我们可以用等差数列求和公式验证原等式是不成立的!这就是说,当n=k+1时,命题也成立.没有用上“假设”,故此法不是数学归纳法请修改为数学归纳法证明 ①当n=1时,左边= , ②假设n=k(k∈N*)时原等式成立 ,即此时,原等式成立。 那么n=k+1时,由 ①②知,对一切正整数n,原等式均正确. 证明 ①当n=1时,左边= , 这才是数学归纳法②假设n=k(k∈N*)时原等式成立 ,即右边= 此时,原等式成立。 那么n=k+1时,这就是说,当n=k+1时,命题也成立.由 ①②知,对一切正整数n,原等式均正确.
1. 试问等式 解:假设当 则当
所以等式对任何 事实上,当 四、深化理解归纳法给出了如下的证明,请问该同学得到的结论正确吗?
成立吗?某同学用数学时等式成立,即时即当时等式也成立.
都成立.时,左边=2,右边=3,左边≠右边,等式不成立.缺少归纳奠基,不属于数学归纳法,是不正确的.
四、深化理解2. 判断证明下面等式是否使用了数学归纳法:证明:①当 右边= ,等式成立. ②假设当 那么当 即当 根据 ①和②,可知等式对一切正整数 左边右边 没有用上“假设”,缺少归纳递推,故此法不是数学归纳法.如何修改?由 时,左边=时等式成立,即时,时,等式也成立.
都成立. 到递推,请学生们自主完成.五、灵活应用 1.已知数列 项和,计算S1, S2 ,S3 ,S4,根据计算结果,
可以看到,上面表示四个结果的分数中,分子与项数一致,
分母可用项数 下面用数学归纳法证明猜想:解析: 时,显然成立;(2)假设 则也成立由(1)和(2)可知 设为数列前猜想表示为,可以猜想(1)当时,对任何的 都成立.的表达式,并用数学归纳法进行证明.五、灵活应用 2.比较 分析:当 时, 时, 时, 时, 时, 时,下面用数学归纳法证明猜想: 时,显然成立;(2)假设 则当 因为即证又所以 故当 由(1)和(2)可知 和的大小.
时,当当当当当猜想当(1)当时,有时,只需证成立.时,猜想成立.对任何的都成立.六、巩固训练 4.设
D.非以上答案 成立时,
起始值至少应取为__. 答案:C答案:8答案:1.若则为( )A.B.C.2.用数学归纳法证明不等式3.用数学归纳法证明:“”时,由不等式成立,推理求证:时,左边应增加的项数是__.
命题成立,”其本质是证明一个递推关系,有了这种向后传递的关系,就能从一个起点不断发展,以至无穷.如果没有它,即使前面验证了命题对许多正整数都成立,也不能保证命题对后面的所有正整数都成立,证明中要注意用假设与凑结论,增强目标意识.七、善思多想 1.数学归纳法的第一步 提示:不一定,要看题目中对 2.为什么可以先假设
的初始值是否一定为1?第一个值
边形的内角和为大,不一定是从1开始取值.如证明值也比较,有时或整数中的最小值,有时是是适合命题的正的要求,时命题也成立就可说明命题成立?
当时命题成立?再证提示:“假设时命题成立,证明当时 1.数学归纳法是一种证明与正整数有关的数学命题的重要 方法.(1)证明当 (2)假设 (3)由(1)和(2)得出结论,缺一不可,注意完整性.2.数学归纳法的证明过程主要有两个步骤一个结论:取第一个值(即命题允许的最小正整数如=1或2等)时结论正确;时,结论成立,当时,利用假设证明结论也成立.课堂小结解析:当n=1时,左边=1+a+a1+1=1+a+a2,故C正确.
答案:C3.用数学归纳法证明“2n+1≥n2+n+2(n∈N*)”时,第一步验证为______________.
解析:由n∈N*可知初始值为1.
答案:当n=1时,左边=4≥右边=4 ,不等式成立解析:由n=k到n=k+1时,左边增加(k+1)2+k2.
答案:(k+1)2+k2九、作业布置必做题:习题2.3 A组 1、2选做题:
1.在各项均为正数的数列 中,数列的前 项和为 ,满足 .
(1)求 的值;
(2)由(1)猜想出数列 的通项公式,并用数学归纳法证明你的猜想.
2.用数学归纳法证明凸 边形的对角线有 条.
求通项公式.
猜想:
学 习 目 标1.了解数学归纳的原理2.能用数学归纳法证明一些简单的数学命题
(多米诺骨牌游戏)
思考:此游戏中,能使所有多米诺骨牌全部倒下的条件?1.第一块骨牌倒下2.任意相邻的两块骨牌,
前一块倒下一定导致后一块倒下递推关系:第k块倒下,相邻的第k+1块也倒下情境引入
1.第一块骨牌倒下2.任意相邻的两块骨牌,
前一块倒下一定导致
后一块倒下
(第k块倒下,相邻的第k+1块也倒下)数列 ,已知
猜想:1. 时,成立2.假设 时成立,那么
时猜想也成立,即
多米诺骨牌一般地证明一个与正整数 1.(归纳奠基)证明当 2.(归纳递推)假设当 有关的命题,可按下列步骤进行:取第一个值 时命题成立;时命题成立,
时命题也成立.
证明当数学归纳法证明:(1)当 左边 所以等式成立.(2)假设当 那么,当 即当 根据(1)和(2),可知等式对任何 时,时等式成立,即时等式也成立.都成立.
数学归纳法
变式练习1 用数学归纳法证明 证明(1)当n=1时,左边=1,右边=1,等式成立.这就是说,当n=k+1时,等式也成立.由(1)和(2),可知等式对任何正整数n都成立.(2)假设当n=k时,等式成立,即递推基础递推依据那么当n=k+1时, 分析下列各题用数学归纳法证明过程中的错误:变式训练2纠错!(1)2+4+6+8+…+2n=n2+n+1(n?N*)证明 :假设当n=k时等式成立,即
2+4+6+8+…+2k=k2+k+1(k?N*)那么,当n=k+1时,有
2+4+6+8+…+2k+2(k+1)
=k2+k+1+2(k+1)
=(k+1)2+(k+1)+1 ,
因此,对于任何n?N*等式都成立。缺乏“递推基础”事实上,我们可以用等差数列求和公式验证原等式是不成立的!这就是说,当n=k+1时,命题也成立.没有用上“假设”,故此法不是数学归纳法请修改为数学归纳法证明 ①当n=1时,左边= , ②假设n=k(k∈N*)时原等式成立 ,即此时,原等式成立。 那么n=k+1时,由 ①②知,对一切正整数n,原等式均正确. 证明 ①当n=1时,左边= , 这才是数学归纳法②假设n=k(k∈N*)时原等式成立 ,即右边= 此时,原等式成立。 那么n=k+1时,这就是说,当n=k+1时,命题也成立.由 ①②知,对一切正整数n,原等式均正确.
1. 试问等式 解:假设当 则当
所以等式对任何 事实上,当 四、深化理解归纳法给出了如下的证明,请问该同学得到的结论正确吗?
成立吗?某同学用数学时等式成立,即时即当时等式也成立.
都成立.时,左边=2,右边=3,左边≠右边,等式不成立.缺少归纳奠基,不属于数学归纳法,是不正确的.
四、深化理解2. 判断证明下面等式是否使用了数学归纳法:证明:①当 右边= ,等式成立. ②假设当 那么当 即当 根据 ①和②,可知等式对一切正整数 左边右边 没有用上“假设”,缺少归纳递推,故此法不是数学归纳法.如何修改?由 时,左边=时等式成立,即时,时,等式也成立.
都成立. 到递推,请学生们自主完成.五、灵活应用 1.已知数列 项和,计算S1, S2 ,S3 ,S4,根据计算结果,
可以看到,上面表示四个结果的分数中,分子与项数一致,
分母可用项数 下面用数学归纳法证明猜想:解析: 时,显然成立;(2)假设 则也成立由(1)和(2)可知 设为数列前猜想表示为,可以猜想(1)当时,对任何的 都成立.的表达式,并用数学归纳法进行证明.五、灵活应用 2.比较 分析:当 时, 时, 时, 时, 时, 时,下面用数学归纳法证明猜想: 时,显然成立;(2)假设 则当 因为即证又所以 故当 由(1)和(2)可知 和的大小.
时,当当当当当猜想当(1)当时,有时,只需证成立.时,猜想成立.对任何的都成立.六、巩固训练 4.设
D.非以上答案 成立时,
起始值至少应取为__. 答案:C答案:8答案:1.若则为( )A.B.C.2.用数学归纳法证明不等式3.用数学归纳法证明:“”时,由不等式成立,推理求证:时,左边应增加的项数是__.
命题成立,”其本质是证明一个递推关系,有了这种向后传递的关系,就能从一个起点不断发展,以至无穷.如果没有它,即使前面验证了命题对许多正整数都成立,也不能保证命题对后面的所有正整数都成立,证明中要注意用假设与凑结论,增强目标意识.七、善思多想 1.数学归纳法的第一步 提示:不一定,要看题目中对 2.为什么可以先假设
的初始值是否一定为1?第一个值
边形的内角和为大,不一定是从1开始取值.如证明值也比较,有时或整数中的最小值,有时是是适合命题的正的要求,时命题也成立就可说明命题成立?
当时命题成立?再证提示:“假设时命题成立,证明当时 1.数学归纳法是一种证明与正整数有关的数学命题的重要 方法.(1)证明当 (2)假设 (3)由(1)和(2)得出结论,缺一不可,注意完整性.2.数学归纳法的证明过程主要有两个步骤一个结论:取第一个值(即命题允许的最小正整数如=1或2等)时结论正确;时,结论成立,当时,利用假设证明结论也成立.课堂小结解析:当n=1时,左边=1+a+a1+1=1+a+a2,故C正确.
答案:C3.用数学归纳法证明“2n+1≥n2+n+2(n∈N*)”时,第一步验证为______________.
解析:由n∈N*可知初始值为1.
答案:当n=1时,左边=4≥右边=4 ,不等式成立解析:由n=k到n=k+1时,左边增加(k+1)2+k2.
答案:(k+1)2+k2九、作业布置必做题:习题2.3 A组 1、2选做题:
1.在各项均为正数的数列 中,数列的前 项和为 ,满足 .
(1)求 的值;
(2)由(1)猜想出数列 的通项公式,并用数学归纳法证明你的猜想.
2.用数学归纳法证明凸 边形的对角线有 条.
