2018年高中数学第三章数系的扩充与复数3.2.1复数的加法与减法课件 新人教B版选修2_2(19张PPT)
文档属性
| 名称 | 2018年高中数学第三章数系的扩充与复数3.2.1复数的加法与减法课件 新人教B版选修2_2(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 239.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-03 00:00:00 | ||
图片预览






文档简介
课件19张PPT。复数的加减运算预备知识一、复数的几何意义
(1)复数z=a+bi与复平面内点Z(a,b)一一对应;
(2)复数z=a+bi与平面向量 一一对应;
(其中O是原点,Z是复数z所对应的点)二、平面向量的加减法
平行四边形法则、三角形法则复数的加法法则规定:(a+bi)+(c+di)=(a+c)+(b+d)i1、(1+2i)+(-2+3i)=口算:2、(-2+3i)+(1+2i)=3、[(-2+3i)+(1+2i)]+(3+4i)
=4、(-2+3i)+[(1+2i)+(3+4i)]
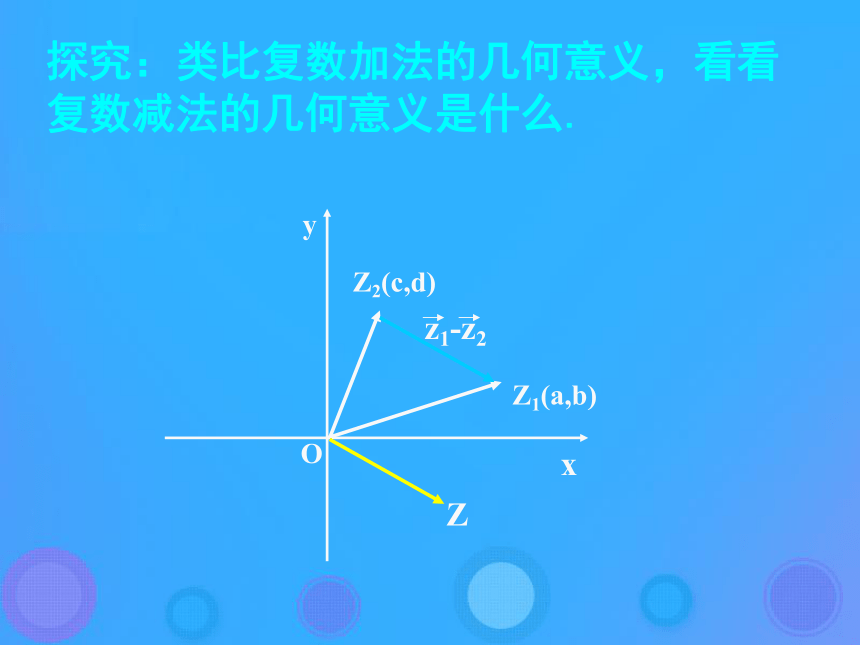
=-1+5i-1+5i(-1+5i)+(3+4i)= 2+9i(-2+3i)+(4+6i) = 2+9i(1)两个复数的和仍是一个复数。(2)复数的加法法则满足交换律、结合律。说明:探究:复数加法的几何意义复数可以用向量表示,如果与这些复数对应的向量不共线,那么这些复数的加法就可以按照向量的平行四边形法则来进行。对应复数(a+c)+(b+d)i复数的减法法则:(a+bi)-(c+di)=(a-c)+(b-d)i注:两个复数的差是仍为复数。口算:(1+2i) -(-2+3i) =3 - i探究:类比复数加法的几何意义,看看复数减法的几何意义是什么.两个复数相加(减)就是分别把实部、虚部对应相加(减),得到一个新的复数,即
(a+bi) ± (c+di) = (a±c) + (b±d)i总结例题讲解例1: 计算(5 - 6i)+(-2 - i)-(3 + 4i)例2:设 z1 = -2 + 5i ,z2 = 3 + 2i,
计算(5 – 2 - 3)+(-6 – 1 - 4)i = -11i(-2 + 5i)-(3 - 2i)=-5 + 7i3.互为共轭复数的两个复数之和一定为实数4.互为共轭复数的两个复数之差一定为虚数2.实数与实数相加为实数, 虚数与虚数相加为虚数判断正误:错误的请举出反例1.实数与虚数相加一定为虚数正确错误正确错误5 - 5i一讲一练1:另解:其对应复数 5-5i=(2-3i)-(-3+2i)分析:一讲一练1:1-7izB - zA结论1:复平面内点A、B对应的复数分别为 zA=3+2i 和 zB= -2+4i,则A、B间的距离是一讲一练2:分析:另解:复平面内点A、B对应的复数分别为 zA=6+i 和 zB= 2-2i,则A、B间的距离是一讲一练2:5一讲一练3:以(1,1)为圆心,半径为1的圆周以(2,3)为圆心,半径为2的圆周思考:你能归纳推导出一个更一般的结论吗?以(a,b)为圆心,半径为r的圆周4小结类比思想:
(代数角度)与实数之间的类比:复数的加减运算遵循实数运算的运算律和运算顺序;
(几何意义)与向量的概念、运算之间的类比。
数形结合:利用复数的几何意义解决距离、轨迹等的问题。不能比较大小
模可以比较大小与复平面的
点一一对应复数与平面向量的性质类比
(1)复数z=a+bi与复平面内点Z(a,b)一一对应;
(2)复数z=a+bi与平面向量 一一对应;
(其中O是原点,Z是复数z所对应的点)二、平面向量的加减法
平行四边形法则、三角形法则复数的加法法则规定:(a+bi)+(c+di)=(a+c)+(b+d)i1、(1+2i)+(-2+3i)=口算:2、(-2+3i)+(1+2i)=3、[(-2+3i)+(1+2i)]+(3+4i)
=4、(-2+3i)+[(1+2i)+(3+4i)]
=-1+5i-1+5i(-1+5i)+(3+4i)= 2+9i(-2+3i)+(4+6i) = 2+9i(1)两个复数的和仍是一个复数。(2)复数的加法法则满足交换律、结合律。说明:探究:复数加法的几何意义复数可以用向量表示,如果与这些复数对应的向量不共线,那么这些复数的加法就可以按照向量的平行四边形法则来进行。对应复数(a+c)+(b+d)i复数的减法法则:(a+bi)-(c+di)=(a-c)+(b-d)i注:两个复数的差是仍为复数。口算:(1+2i) -(-2+3i) =3 - i探究:类比复数加法的几何意义,看看复数减法的几何意义是什么.两个复数相加(减)就是分别把实部、虚部对应相加(减),得到一个新的复数,即
(a+bi) ± (c+di) = (a±c) + (b±d)i总结例题讲解例1: 计算(5 - 6i)+(-2 - i)-(3 + 4i)例2:设 z1 = -2 + 5i ,z2 = 3 + 2i,
计算(5 – 2 - 3)+(-6 – 1 - 4)i = -11i(-2 + 5i)-(3 - 2i)=-5 + 7i3.互为共轭复数的两个复数之和一定为实数4.互为共轭复数的两个复数之差一定为虚数2.实数与实数相加为实数, 虚数与虚数相加为虚数判断正误:错误的请举出反例1.实数与虚数相加一定为虚数正确错误正确错误5 - 5i一讲一练1:另解:其对应复数 5-5i=(2-3i)-(-3+2i)分析:一讲一练1:1-7izB - zA结论1:复平面内点A、B对应的复数分别为 zA=3+2i 和 zB= -2+4i,则A、B间的距离是一讲一练2:分析:另解:复平面内点A、B对应的复数分别为 zA=6+i 和 zB= 2-2i,则A、B间的距离是一讲一练2:5一讲一练3:以(1,1)为圆心,半径为1的圆周以(2,3)为圆心,半径为2的圆周思考:你能归纳推导出一个更一般的结论吗?以(a,b)为圆心,半径为r的圆周4小结类比思想:
(代数角度)与实数之间的类比:复数的加减运算遵循实数运算的运算律和运算顺序;
(几何意义)与向量的概念、运算之间的类比。
数形结合:利用复数的几何意义解决距离、轨迹等的问题。不能比较大小
模可以比较大小与复平面的
点一一对应复数与平面向量的性质类比
