2018年高中数学第一章导数及其应用1.1.2瞬时速度与导数课件 新人教B版选修2_2(28张PPT)
文档属性
| 名称 | 2018年高中数学第一章导数及其应用1.1.2瞬时速度与导数课件 新人教B版选修2_2(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 495.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-03 09:06:40 | ||
图片预览






文档简介
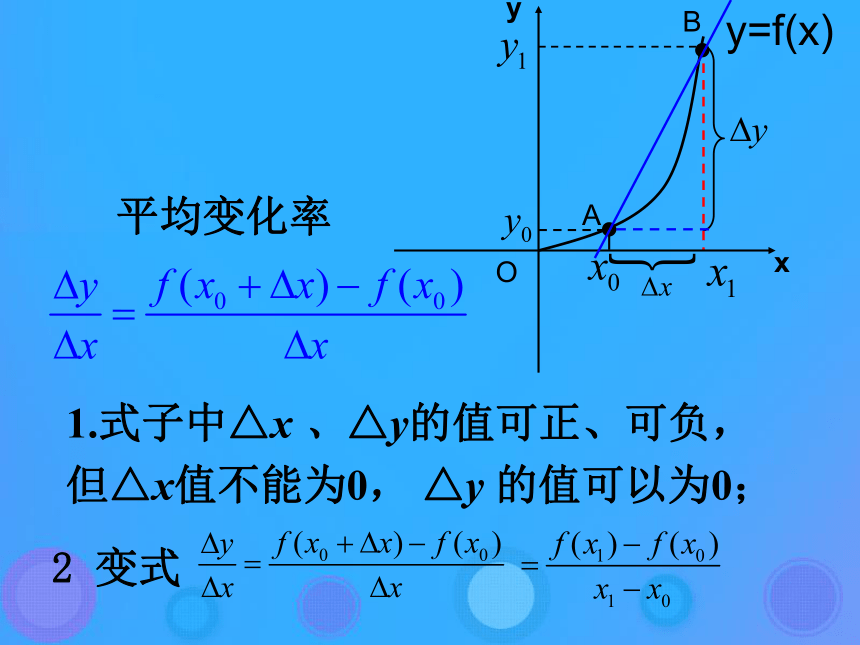
课件28张PPT。1.1.2瞬时速度与导数平均变化率的概念: 一般地,已知函数y=f(x),x0,x1是其定义域内不同的两点 则当△x≠0时,商
称作函数y=f(x)在区间[x0,x0+△x]
(或[x0+△x,x0])的平均变化率。记△x=x1-x0=f(x0+△x)-f(x0).
则△y=y1-y0=f(x1)-f(x0)
1.式子中△x 、△y的值可正、可负,但△x值不能为0, △y 的值可以为0;
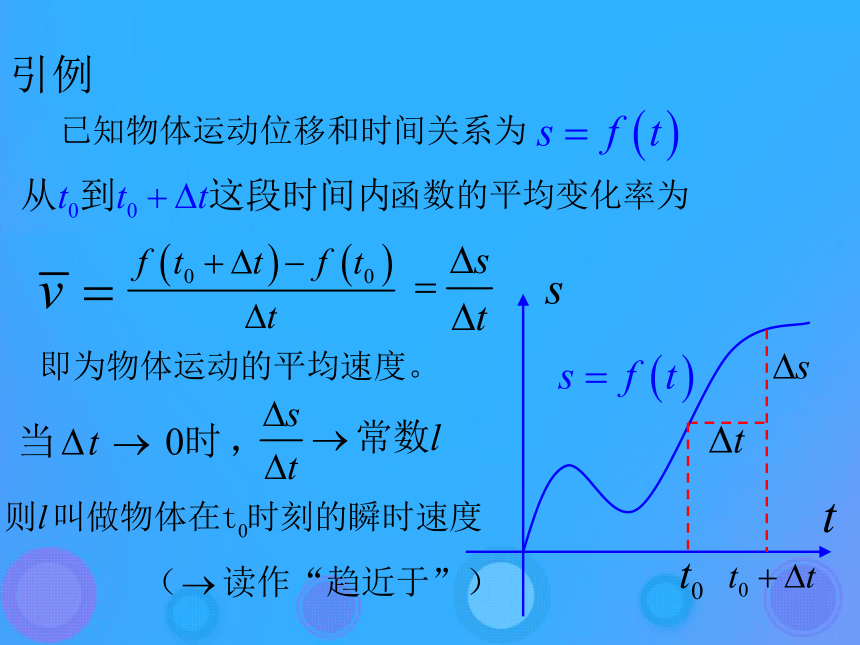
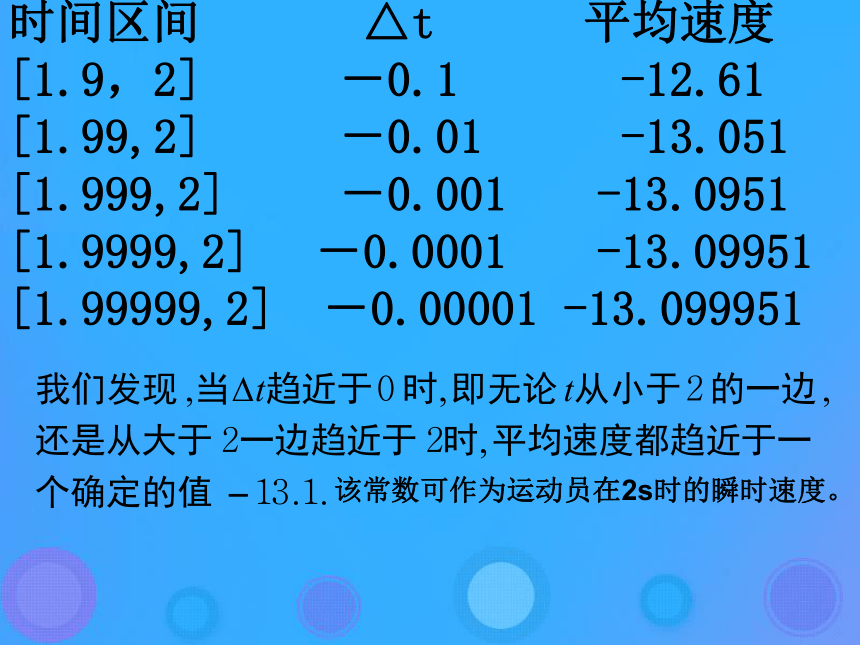
2 变式平均变化率Oxyy=f(x)BA引例即为物体运动的平均速度。问题情境: 跳水运动员从10m高跳台腾空到入水的过程中,不同时刻的速度是不同的。假设t 秒后运动员相对于水面的高度为H(t)=-4.9t2+6.5t+10,试确定t=2s时运动员的速度。(1)计算运动员在2s到2.1s(t∈[2,2.1])内的平均速度。(2)计算运动员在2s到2+⊿t s(t∈[2,2+⊿t])内的平均速度。时间区间 △t 平均速度 [1.9,2] -0.1 -12.61 [1.99,2] -0.01 -13.051 [1.999,2] -0.001 -13.0951 [1.9999,2] -0.0001 -13.09951 [1.99999,2] -0.00001 -13.099951 该常数可作为运动员在2s时的瞬时速度。 设物体作直线运动所经过的路程为s=h(t)。
以t0为起始时刻,物体在?t时间内的平均速度为就是物体在t0时刻的瞬时速度,即 所以当?t?0时,比值瞬时速度函数的瞬时变化率: 函数y=f(x),在x0及其附近有意义,自变量在x=x0附近改变量为△x
平均变化率为f(x0+△x)-f(x0).
则函数值相应的改变△y=常数 常数 称为函数f(x)在点x0的瞬时变化率 上述过程记作即 如果函数 f(x)在开区间 (a,b) 内每一点都可导,就说f(x)在开区间 (a,b)内可导.这时,对于开区间 (a,b)内每一个确定的值 x,都对应着一个确定的导数 这样就在开区间(a,b)内构成了一个新的函数,我们把这一新函数叫做 f(x) 在开区间(a,b)内的导函数,简称为导数,记作例1.求y=x2在点x=1处的导数解:由定义求导数(三步法)步骤:变式1.求y=x2+2在点x=1处的导数解:(求极限时,若经整理后分母不含 ,则令其为0即可) 练习:(1)求函数y=x2在x=1处的导数;
(2)求函数 在x=2处的导数.例1.火箭竖直向上发射,熄火时向上的速度达到100m/s,试问熄火后多长时间火箭向上的速度为0? 解:火箭的运动方程为h(t)=100t- gt2,在t附近的平均变化率为=100-gt- g△t。 当△t→0时,上式趋近于100-gt。
可见t时刻的瞬时速度h’(t)=100-gt。 令h’(t)=100-gt=0,解得 所以火箭熄火后约10.2s向上的速度变为0.例3. 求函数y=x2在点x=3处的导数。解:因为△y=(3+△x)2-32=6△x+(△x)2.所以=6+△x,令△x→0,→6所以函数y=x2在点x=3处的导数为6.例4.质点M按规律s(t)=at2+1作直线运动,若质点M在t=2时的瞬时速度为8m/s,求常数a的值。解:因为△s=a(t+△t)2+1-(at2+1)
=2at△t+a(△t)2,所以 =2at+a△t, 当△t→0时,s′=2at, 由题意知t=2时,s′=8,即4a=8,解得a=2.例5.已知y=ax2+bx+c,求y′及y′|x=2。解:△y=a(x+△x)2+b(x+△x)+c-(ax2+bx+c)
=(2ax+b)△x+a(△x)2, =(2ax+b)+a△x,当△x→0时,y′= 2ax+b,当x=2时,y′|x=2=4a+b。练习题1.一物体的运动方程是s=3+t2,则在一小段时间[2, 2.1]内相应的平均速度为( )
A.0.41 B.3
C.4 D.4.1 D2.设y=f(x)函数可导,则
等于( )
A.f ′(1) B.不存在
C. f ′(1) D.3f ′(1)C3.设 ,则 等于( )
A. B.
C. D.C4.若f(x)=x3,f ′(x0)=3,则x0的值是( )
A.1 B.-1
C.±1 D.C5.设函数f(x)=ax3+2,若f ′(-1)=3,则a=__________。16.函数y=2mx+n的瞬时变化率是 . 2m7.函数 在x=1处的导数是
. 小结: 函数的瞬时变化率、导数 函数f(x)在x0处的瞬时变化率就是在x=x0处的导数 求导数的一般步骤
称作函数y=f(x)在区间[x0,x0+△x]
(或[x0+△x,x0])的平均变化率。记△x=x1-x0=f(x0+△x)-f(x0).
则△y=y1-y0=f(x1)-f(x0)
1.式子中△x 、△y的值可正、可负,但△x值不能为0, △y 的值可以为0;
2 变式平均变化率Oxyy=f(x)BA引例即为物体运动的平均速度。问题情境: 跳水运动员从10m高跳台腾空到入水的过程中,不同时刻的速度是不同的。假设t 秒后运动员相对于水面的高度为H(t)=-4.9t2+6.5t+10,试确定t=2s时运动员的速度。(1)计算运动员在2s到2.1s(t∈[2,2.1])内的平均速度。(2)计算运动员在2s到2+⊿t s(t∈[2,2+⊿t])内的平均速度。时间区间 △t 平均速度 [1.9,2] -0.1 -12.61 [1.99,2] -0.01 -13.051 [1.999,2] -0.001 -13.0951 [1.9999,2] -0.0001 -13.09951 [1.99999,2] -0.00001 -13.099951 该常数可作为运动员在2s时的瞬时速度。 设物体作直线运动所经过的路程为s=h(t)。
以t0为起始时刻,物体在?t时间内的平均速度为就是物体在t0时刻的瞬时速度,即 所以当?t?0时,比值瞬时速度函数的瞬时变化率: 函数y=f(x),在x0及其附近有意义,自变量在x=x0附近改变量为△x
平均变化率为f(x0+△x)-f(x0).
则函数值相应的改变△y=常数 常数 称为函数f(x)在点x0的瞬时变化率 上述过程记作即 如果函数 f(x)在开区间 (a,b) 内每一点都可导,就说f(x)在开区间 (a,b)内可导.这时,对于开区间 (a,b)内每一个确定的值 x,都对应着一个确定的导数 这样就在开区间(a,b)内构成了一个新的函数,我们把这一新函数叫做 f(x) 在开区间(a,b)内的导函数,简称为导数,记作例1.求y=x2在点x=1处的导数解:由定义求导数(三步法)步骤:变式1.求y=x2+2在点x=1处的导数解:(求极限时,若经整理后分母不含 ,则令其为0即可) 练习:(1)求函数y=x2在x=1处的导数;
(2)求函数 在x=2处的导数.例1.火箭竖直向上发射,熄火时向上的速度达到100m/s,试问熄火后多长时间火箭向上的速度为0? 解:火箭的运动方程为h(t)=100t- gt2,在t附近的平均变化率为=100-gt- g△t。 当△t→0时,上式趋近于100-gt。
可见t时刻的瞬时速度h’(t)=100-gt。 令h’(t)=100-gt=0,解得 所以火箭熄火后约10.2s向上的速度变为0.例3. 求函数y=x2在点x=3处的导数。解:因为△y=(3+△x)2-32=6△x+(△x)2.所以=6+△x,令△x→0,→6所以函数y=x2在点x=3处的导数为6.例4.质点M按规律s(t)=at2+1作直线运动,若质点M在t=2时的瞬时速度为8m/s,求常数a的值。解:因为△s=a(t+△t)2+1-(at2+1)
=2at△t+a(△t)2,所以 =2at+a△t, 当△t→0时,s′=2at, 由题意知t=2时,s′=8,即4a=8,解得a=2.例5.已知y=ax2+bx+c,求y′及y′|x=2。解:△y=a(x+△x)2+b(x+△x)+c-(ax2+bx+c)
=(2ax+b)△x+a(△x)2, =(2ax+b)+a△x,当△x→0时,y′= 2ax+b,当x=2时,y′|x=2=4a+b。练习题1.一物体的运动方程是s=3+t2,则在一小段时间[2, 2.1]内相应的平均速度为( )
A.0.41 B.3
C.4 D.4.1 D2.设y=f(x)函数可导,则
等于( )
A.f ′(1) B.不存在
C. f ′(1) D.3f ′(1)C3.设 ,则 等于( )
A. B.
C. D.C4.若f(x)=x3,f ′(x0)=3,则x0的值是( )
A.1 B.-1
C.±1 D.C5.设函数f(x)=ax3+2,若f ′(-1)=3,则a=__________。16.函数y=2mx+n的瞬时变化率是 . 2m7.函数 在x=1处的导数是
. 小结: 函数的瞬时变化率、导数 函数f(x)在x0处的瞬时变化率就是在x=x0处的导数 求导数的一般步骤
