2018年高中数学第一章导数及其应用1.3.1利用导数判断函数的单调性课件 新人教B版选修2_2(15张PPT)
文档属性
| 名称 | 2018年高中数学第一章导数及其应用1.3.1利用导数判断函数的单调性课件 新人教B版选修2_2(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 843.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-03 00:00:00 | ||
图片预览





文档简介
课件15张PPT。§1.3 导数的应用
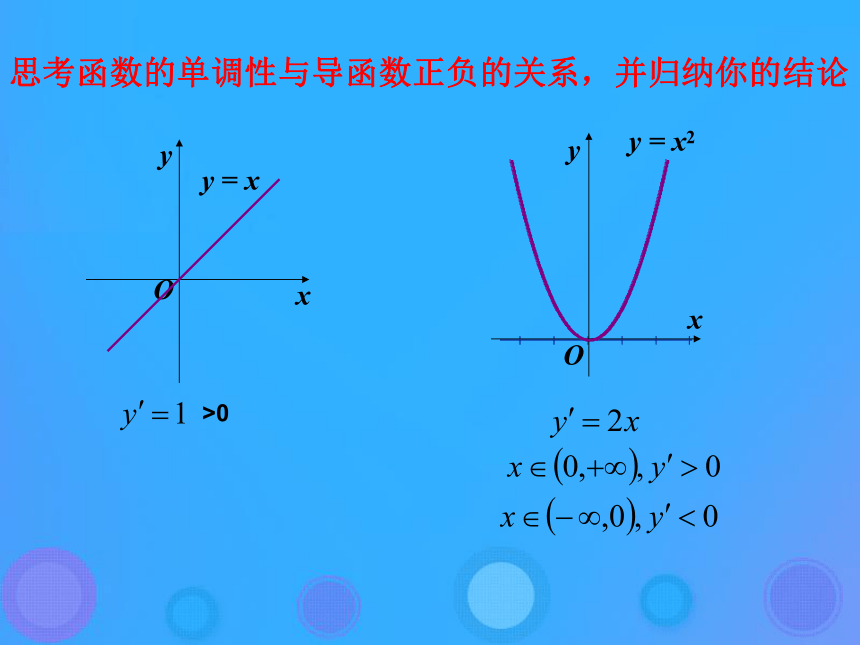
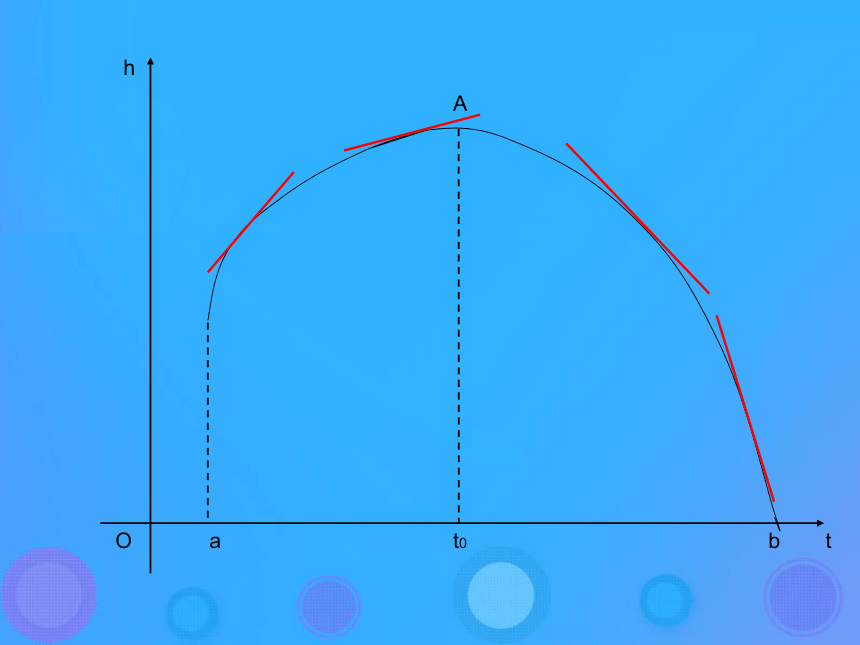
§1.3.1 利用导数判断函数的单调性复习回顾 增函数、减函数的定义: 竖直上抛一个小沙袋,沙袋的高度h是时间t的函数,设h=h(t) 考虑沙袋在区间(a,t0)的运动情况: (1)瞬时速度是正还是负? (2)在区间内的导函数值是正值还是负值? (3)此区间内,h=h(t)是增函数还是减函数?增函数正再考察沙袋在区间(t0,b)的运动情况?(1)负(3)减函数xyOy = x2思考函数的单调性与导函数正负的关系,并归纳你的结论yOy = xx>0 注意:导函数看正负 原函数看增减用导数的正负判断函数单调性的法则:hOat0btA例1:求函数 的单调区间 题型一:求函数的单调区间利用导数求函数单调区间的一般过程: 先求函数f(x)的定义域 注:多个单调区间不能用“并集”连接,要用“和”单调增区间为
单调减区间为跟踪训练2: 求函数 的单调区间单调增区间为 ,单调减区间为例2 已知函数y=f(x)的图象如图所示,则函数y=f ′(x)的
图象可能是图中的( )C题型二:由y=f(x)的增减判断函数y=f′(x)的正负情况跟踪训练 已知y=f ′(x)的图象如图所示,则y=f(x)的图象最有可能是如图所示的( )C例3.如图,设有圆C和定点O,当l 从l0 开始在平面上绕O点匀速旋转(旋转角度不超过90°)时,它扫过的圆内阴影部分的面积S是时间t的函数,它的图象大致是下列四种情况中的哪一种?D题型三:函数的变化快慢与导数的关系SOt小结:1.函数单调性与导数符号的关系是:2.判定函数单调区间的步骤: ①求出函数的定义域; ②求出函数的导数f ?(x); ③在函数的定义域内解f ?(x)>0和f ?(x)<0; ④确定函数f(x)的单调区间。综合提高练:求函数 的单调区间
§1.3.1 利用导数判断函数的单调性复习回顾 增函数、减函数的定义: 竖直上抛一个小沙袋,沙袋的高度h是时间t的函数,设h=h(t) 考虑沙袋在区间(a,t0)的运动情况: (1)瞬时速度是正还是负? (2)在区间内的导函数值是正值还是负值? (3)此区间内,h=h(t)是增函数还是减函数?增函数正再考察沙袋在区间(t0,b)的运动情况?(1)负(3)减函数xyOy = x2思考函数的单调性与导函数正负的关系,并归纳你的结论yOy = xx>0 注意:导函数看正负 原函数看增减用导数的正负判断函数单调性的法则:hOat0btA例1:求函数 的单调区间 题型一:求函数的单调区间利用导数求函数单调区间的一般过程: 先求函数f(x)的定义域 注:多个单调区间不能用“并集”连接,要用“和”单调增区间为
单调减区间为跟踪训练2: 求函数 的单调区间单调增区间为 ,单调减区间为例2 已知函数y=f(x)的图象如图所示,则函数y=f ′(x)的
图象可能是图中的( )C题型二:由y=f(x)的增减判断函数y=f′(x)的正负情况跟踪训练 已知y=f ′(x)的图象如图所示,则y=f(x)的图象最有可能是如图所示的( )C例3.如图,设有圆C和定点O,当l 从l0 开始在平面上绕O点匀速旋转(旋转角度不超过90°)时,它扫过的圆内阴影部分的面积S是时间t的函数,它的图象大致是下列四种情况中的哪一种?D题型三:函数的变化快慢与导数的关系SOt小结:1.函数单调性与导数符号的关系是:2.判定函数单调区间的步骤: ①求出函数的定义域; ②求出函数的导数f ?(x); ③在函数的定义域内解f ?(x)>0和f ?(x)<0; ④确定函数f(x)的单调区间。综合提高练:求函数 的单调区间
