高中数学第2章圆锥曲线与方程2.5圆锥曲线的统一定义课件 苏教版选修2_1(14张PPT)
文档属性
| 名称 | 高中数学第2章圆锥曲线与方程2.5圆锥曲线的统一定义课件 苏教版选修2_1(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 255.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-03 00:00:00 | ||
图片预览





文档简介
课件14张PPT。圆锥曲线的综合应用
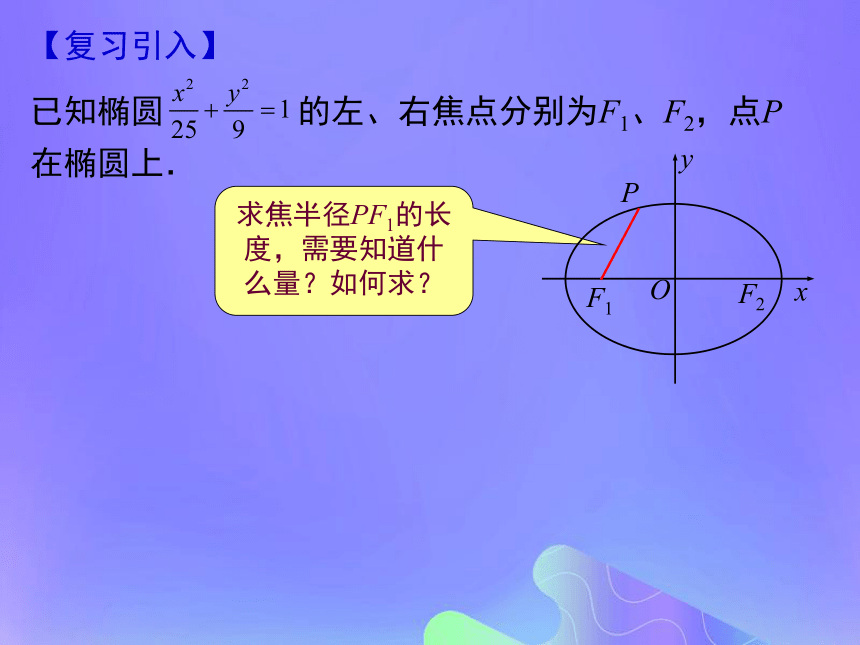
—— 焦点弦问题 【课前热身】 1、已知双曲线 上的点P到右焦点的距离为4,则P到左准线的距离是 .2、椭圆 上一点M到左焦点F1的距离是2,N是MF1的中点,O为坐标原点,则ON= .3、若抛物线 上两点A、B到焦点的距离之和是5,则线段AB中点到y轴的距离为 . 4、设AB是过椭圆 右焦点的弦,那么以AB为直径的圆与椭圆的右准线的位置关系是 . 【复习引入】 已知椭圆 的左、右焦点分别为F1、F2,点P在椭圆上. 求焦半径PF1的长度,需要知道什么量?如何求?【复习引入】 已知椭圆 的左、右焦点分别为F1、F2,点P在椭圆上. (1)若点P的横坐标是-2,求PF1; (2)若PF1所在直线的倾斜角为60°,
求PF1. 【复习引入】 已知椭圆 的左、右焦点分别为F1、F2,点P在椭圆上. (2)若PF1所在直线的倾斜角为60°,
求PF1. 追问:
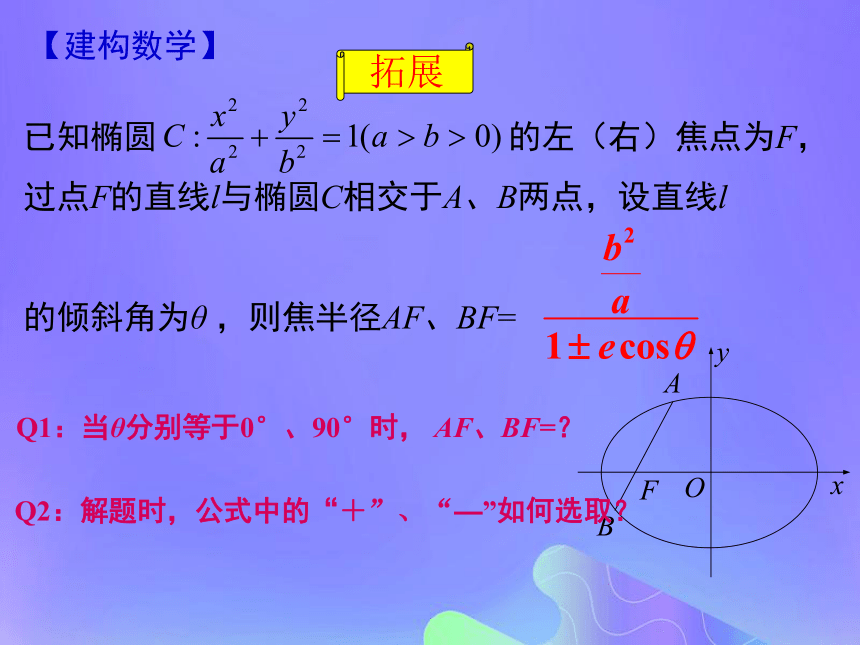
若直线PF1与椭圆的另一个交点为Q,则PF1—QF1 =?【建构数学】 已知椭圆 的左(右)焦点为F,过点F的直线l与椭圆C相交于A、B两点,设直线l
的倾斜角为θ ,则焦半径AF、BF=拓展Q1:当θ分别等于0°、90°时, AF、BF=?Q2:解题时,公式中的“+”、“—”如何选取?已知椭圆 的左、右焦点分别为F1、F2,点P在椭圆上. QQ直线PF1与椭圆的另一个交点为Q,则PF1—QF1 =?例1、(根据2012年江苏卷改编) 【数学应用】 如图,椭圆 的左、右焦点分别为F1、F2 ,A、B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行. (1)若 ,求直线AF1倾斜角的余弦值; (2)设AF2与BF1交于点P,
求证: 是定值. 总结例2(1)若θ=60°时,AF=2FB,求离心率e的值; 拓展设 ,则e, cosθ, λ这三者之间的等量关系式是:已知椭圆 的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,设直线l的倾斜角为θ. 练习(2)求证: ;(3)过点F又作一条直线l’交椭圆C于D、E两点,且l’⊥l,当θ变化时,求AB+DE的最小值. 例2已知椭圆 的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,设直线l的倾斜角为θ. 总结【巩固内化】 1、已知椭圆C: 离心率为 , 过右焦点F且斜率为k(k>0)的直线与C交于A、B两点, 若 , 则k= .2、设F是抛物线C:y2=4x的焦点,过F且斜率为1的直线交C于A、B两点,设FA>FB,则FA与FB的比值等于 . 3、经过双曲线 的右焦点F作倾斜角为105°的直线,交双曲线于P、Q两点,则PF·FQ的值为 . 4、设F1、F2是椭圆 的左、右焦点,过F1、F2作两条互相垂直的直线分别与椭圆相交于D、B和A、C,求四边形ABCD面积的最小值. 已知椭圆 的左(右)焦点为F,过点F的直线l与椭圆C相交于A、B两点,设直线l
的倾斜角为θ ,则(2)焦点弦AB=(1)焦半径AF、BF=(3)离心率e、倾斜角的余弦值cosθ、AF与FB的比值λ(λ >1)之间的关系:【归纳总结】本节课,哪些题型、解法、公式、图形等给你留下了深刻印象?PS:双曲线中有类似的结论吗?【归纳总结】1、数学知识层面: 运用圆锥曲线的第二定义将焦半径转化为点到相应准线的距离,构造几何图形(直角三角形或直角梯形)求解焦半径的长度,并以此求焦半径的和(如焦点弦长)、差、积与商.2、数学方法层面: 数形结合、分类讨论、归纳类比……
—— 焦点弦问题 【课前热身】 1、已知双曲线 上的点P到右焦点的距离为4,则P到左准线的距离是 .2、椭圆 上一点M到左焦点F1的距离是2,N是MF1的中点,O为坐标原点,则ON= .3、若抛物线 上两点A、B到焦点的距离之和是5,则线段AB中点到y轴的距离为 . 4、设AB是过椭圆 右焦点的弦,那么以AB为直径的圆与椭圆的右准线的位置关系是 . 【复习引入】 已知椭圆 的左、右焦点分别为F1、F2,点P在椭圆上. 求焦半径PF1的长度,需要知道什么量?如何求?【复习引入】 已知椭圆 的左、右焦点分别为F1、F2,点P在椭圆上. (1)若点P的横坐标是-2,求PF1; (2)若PF1所在直线的倾斜角为60°,
求PF1. 【复习引入】 已知椭圆 的左、右焦点分别为F1、F2,点P在椭圆上. (2)若PF1所在直线的倾斜角为60°,
求PF1. 追问:
若直线PF1与椭圆的另一个交点为Q,则PF1—QF1 =?【建构数学】 已知椭圆 的左(右)焦点为F,过点F的直线l与椭圆C相交于A、B两点,设直线l
的倾斜角为θ ,则焦半径AF、BF=拓展Q1:当θ分别等于0°、90°时, AF、BF=?Q2:解题时,公式中的“+”、“—”如何选取?已知椭圆 的左、右焦点分别为F1、F2,点P在椭圆上. QQ直线PF1与椭圆的另一个交点为Q,则PF1—QF1 =?例1、(根据2012年江苏卷改编) 【数学应用】 如图,椭圆 的左、右焦点分别为F1、F2 ,A、B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行. (1)若 ,求直线AF1倾斜角的余弦值; (2)设AF2与BF1交于点P,
求证: 是定值. 总结例2(1)若θ=60°时,AF=2FB,求离心率e的值; 拓展设 ,则e, cosθ, λ这三者之间的等量关系式是:已知椭圆 的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,设直线l的倾斜角为θ. 练习(2)求证: ;(3)过点F又作一条直线l’交椭圆C于D、E两点,且l’⊥l,当θ变化时,求AB+DE的最小值. 例2已知椭圆 的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,设直线l的倾斜角为θ. 总结【巩固内化】 1、已知椭圆C: 离心率为 , 过右焦点F且斜率为k(k>0)的直线与C交于A、B两点, 若 , 则k= .2、设F是抛物线C:y2=4x的焦点,过F且斜率为1的直线交C于A、B两点,设FA>FB,则FA与FB的比值等于 . 3、经过双曲线 的右焦点F作倾斜角为105°的直线,交双曲线于P、Q两点,则PF·FQ的值为 . 4、设F1、F2是椭圆 的左、右焦点,过F1、F2作两条互相垂直的直线分别与椭圆相交于D、B和A、C,求四边形ABCD面积的最小值. 已知椭圆 的左(右)焦点为F,过点F的直线l与椭圆C相交于A、B两点,设直线l
的倾斜角为θ ,则(2)焦点弦AB=(1)焦半径AF、BF=(3)离心率e、倾斜角的余弦值cosθ、AF与FB的比值λ(λ >1)之间的关系:【归纳总结】本节课,哪些题型、解法、公式、图形等给你留下了深刻印象?PS:双曲线中有类似的结论吗?【归纳总结】1、数学知识层面: 运用圆锥曲线的第二定义将焦半径转化为点到相应准线的距离,构造几何图形(直角三角形或直角梯形)求解焦半径的长度,并以此求焦半径的和(如焦点弦长)、差、积与商.2、数学方法层面: 数形结合、分类讨论、归纳类比……
