人教版数学七年级下册5.2 平行线及其判定同步测试(附答案)
文档属性
| 名称 | 人教版数学七年级下册5.2 平行线及其判定同步测试(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 480.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-02 22:54:09 | ||
图片预览

文档简介
人教版数学七年级下册5.2 平行线及其判定 同步测试
一、选择题
1.在同一平面内的两条不重合的直线的位置关系( C )
A.有两种:垂直或相交 B.有三种:平行,垂直或相交
C.有两种:平行或相交 D.有两种:平行或垂直
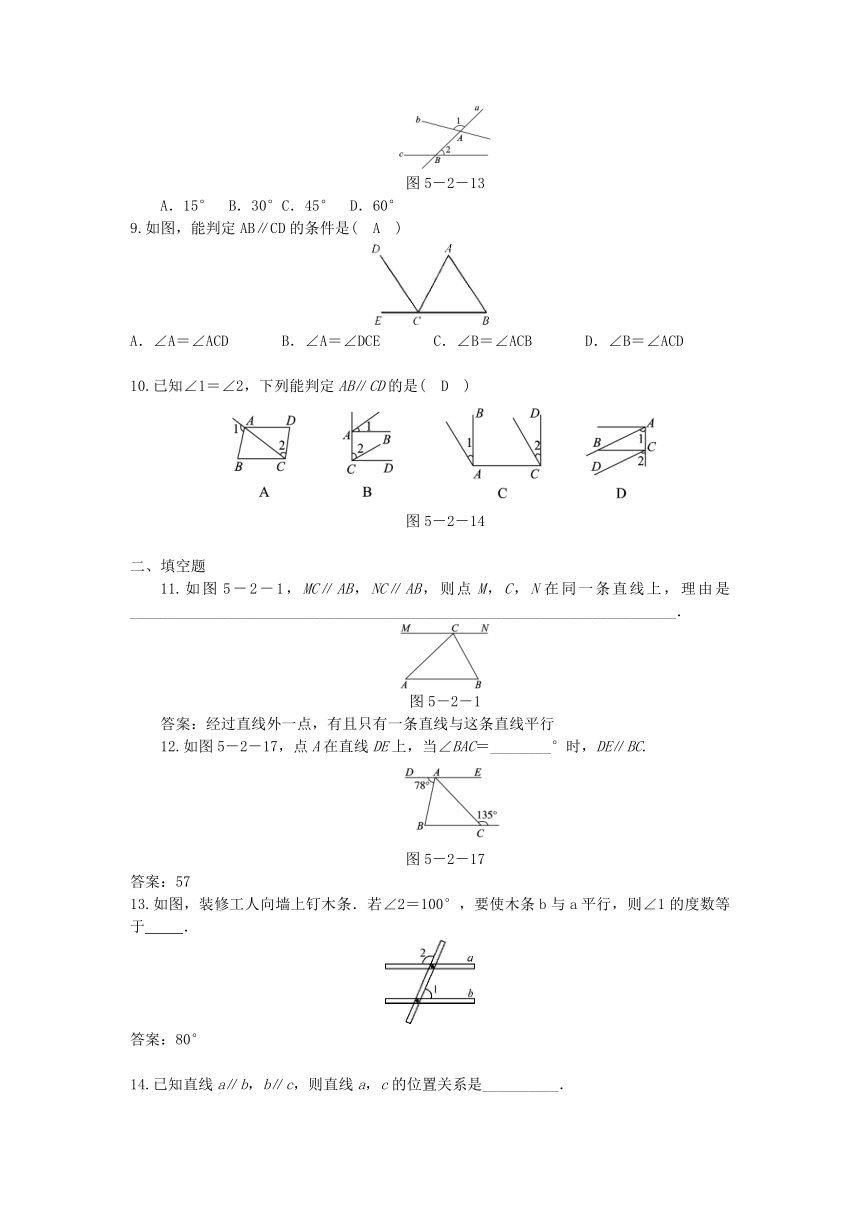
2.图5-2-10是我们学过的用直尺和三角尺画平行线的方法示意图,画图原理是( A )
图5-2-10
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.如果两条直线都和第三条直线平行,那么这两条直线平行
3.在同一平面内,互不重合的三条直线公共点的个数是( D )
A.只可能是0个、1个或3个
B.只可能是0个、1个或2个
C.只可能是0个、2个或3个
D.0个、1个、2个或3个都有可能
4.若直线a∥b,b∥c,则a∥c的依据是( D )
A.平行公理 B.等量代换 C.等式的性质 D.平行于同一条直线的两条直线平行
5.下列选项中,两条直线可能不平行的是( D )
图5-2-2
6.如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( C )
A.∠2=35° B.∠2=45° C.∠2=55° D.∠2=125°
7.下列说法正确的是( D )
A.不相交的两条线段是平行线
B.不相交的两条直线是平行线
C.不相交的两条射线是平行线
D.在同一平面内,不相交的两条直线是平行线
8.如图5-2-13,直线a与直线b相交于点A,与直线c相交于点B,∠1=120°,∠2=45°.若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( A )
图5-2-13
A.15° B.30°C.45° D.60°
9.如图,能判定AB∥CD的条件是( A )
A.∠A=∠ACD B.∠A=∠DCE C.∠B=∠ACB D.∠B=∠ACD
10.已知∠1=∠2,下列能判定AB∥CD的是( D )
图5-2-14
填空题
11.如图5-2-1,MC∥AB,NC∥AB,则点M,C,N在同一条直线上,理由是________________________________________________________________________.
图5-2-1
答案:经过直线外一点,有且只有一条直线与这条直线平行
12.如图5-2-17,点A在直线DE上,当∠BAC=________°时,DE∥BC.
图5-2-17
答案:57
13.如图,装修工人向墙上钉木条.若∠2=100°,要使木条b与a平行,则∠1的度数等于 .
答案:80°
14.已知直线a∥b,b∥c,则直线a,c的位置关系是__________.
答案:a∥c
15.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是 .
答案:153°
16.如图5-2-3是一个长方体,用符号表示下列两棱的位置关系:
图5-2-3
AB________BC;AB________EF;AB________CD.
答案:⊥ ∥ ∥
解答题
17.读下列语句,并画出图形.
P是直线AB外一点,直线CD经过点P且与直线AB平行,直线EF也经过点P且与直线AB垂直.
解:如图所示:
18.完成下面的推理过程:
如图,CB平分∠ACD,∠1=∠3.试说明:AB∥CD.
解:∵CB平分∠ACD,
∴∠1=∠2(角平分线的定义).
∵∠1=∠3,
∴∠2=∠3.
∴AB∥CD(内错角相等,两直线平行).
19.如图5-2-15,PE⊥MN,QF⊥MN,∠1=∠2,直线AB与CD平行吗?为什么?
图5-2-15
解:AB∥CD.理由如下:
∵PE⊥MN,QF⊥MN(已知),
∴∠MEP=∠MFQ=90°(垂直的定义).
又∵∠1=∠2(已知),
∴∠MEP-∠1=∠MFQ-∠2(等式的性质),
即∠MEB=∠MFD,
∴AB∥CD(同位角相等,两直线平行).
20.如图,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明:AB∥CD.
解:∵OF平分∠EOD,∠FOD=25°,
∴∠EOD=2∠FOD=50°.
又∵∠OEB=130°,
∴∠OEB+∠EOD=180°.
∴AB∥CD(同旁内角互补,两直线平行).
21.如图5-2-9,P是线段AB的中点,过点P画BC的平行线交AC于点Q,再过点Q画AB的平行线交BC于点S.
(1)用刻度尺测量后确定AQ与QC,CS与BS的数量关系;
(2)用刻度尺测量后确定PQ与BC,QS与AB的数量关系,你发现了什么?用简洁的语言把你发现的规律叙述出来.
图5-2-9
解:所画图形如图所示.
(1)经测量得到AQ=QC,
CS=BS.
(2)经测量得到PQ=BC,QS=AB.
22.经过三角形一边的中点,画另一边的平行线,则这条平行线平分第三边;三角形两边中点之间线段的长度等于第三边长度的一半.
如图,要判定AB∥CD,需要哪些条件?根据是什么?
解:①若考虑截线AD,则需∠D+∠DAB=180°,根据是同旁内角互补,两直线平行.
②若考虑截线AE,则需∠CEA+∠EAB=180°,根据是同旁内角互补,两直线平行或∠DEA=∠EAB,根据是内错角相等,两直线平行.
③若考虑截线AC,则需∠DCA=∠CAB,根据是内错角相等,两直线平行.
④若考虑截线FC,则需∠DCF+∠AFC=180°,根据是同旁内角互补,两直线平行或∠DCF=∠BFC,根据是内错角相等,两直线平行.
⑤若考虑截线BC,则需∠DCB+∠B=180°,根据是同旁内角互补,两直线平行.
23.小明到工厂进行社会实践活动时,发现工人师傅生产了一种如图5-2-23所示的零件,要求AB∥CD,∠BAE=35°,∠AED=90°.小明发现工人师傅只是量出∠BAE=35°,∠AED=90°后,又量了∠EDC=55°,就说AB与CD肯定是平行的.你知道原因吗?
图5-2-23
解:以E为顶点,AE为一边,在∠AED的内部作∠AEM=∠BAE=35°,∴AB∥EM(内错角相等,两直线平行).
又∵∠AED=90°,∴∠DEM=∠EDC=55°,
∴CD∥EM(内错角相等,两直线平行),
∴AB∥CD(平行于同一条直线的两直线平行).
一、选择题
1.在同一平面内的两条不重合的直线的位置关系( C )
A.有两种:垂直或相交 B.有三种:平行,垂直或相交
C.有两种:平行或相交 D.有两种:平行或垂直
2.图5-2-10是我们学过的用直尺和三角尺画平行线的方法示意图,画图原理是( A )
图5-2-10
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.如果两条直线都和第三条直线平行,那么这两条直线平行
3.在同一平面内,互不重合的三条直线公共点的个数是( D )
A.只可能是0个、1个或3个
B.只可能是0个、1个或2个
C.只可能是0个、2个或3个
D.0个、1个、2个或3个都有可能
4.若直线a∥b,b∥c,则a∥c的依据是( D )
A.平行公理 B.等量代换 C.等式的性质 D.平行于同一条直线的两条直线平行
5.下列选项中,两条直线可能不平行的是( D )
图5-2-2
6.如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( C )
A.∠2=35° B.∠2=45° C.∠2=55° D.∠2=125°
7.下列说法正确的是( D )
A.不相交的两条线段是平行线
B.不相交的两条直线是平行线
C.不相交的两条射线是平行线
D.在同一平面内,不相交的两条直线是平行线
8.如图5-2-13,直线a与直线b相交于点A,与直线c相交于点B,∠1=120°,∠2=45°.若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( A )
图5-2-13
A.15° B.30°C.45° D.60°
9.如图,能判定AB∥CD的条件是( A )
A.∠A=∠ACD B.∠A=∠DCE C.∠B=∠ACB D.∠B=∠ACD
10.已知∠1=∠2,下列能判定AB∥CD的是( D )
图5-2-14
填空题
11.如图5-2-1,MC∥AB,NC∥AB,则点M,C,N在同一条直线上,理由是________________________________________________________________________.
图5-2-1
答案:经过直线外一点,有且只有一条直线与这条直线平行
12.如图5-2-17,点A在直线DE上,当∠BAC=________°时,DE∥BC.
图5-2-17
答案:57
13.如图,装修工人向墙上钉木条.若∠2=100°,要使木条b与a平行,则∠1的度数等于 .
答案:80°
14.已知直线a∥b,b∥c,则直线a,c的位置关系是__________.
答案:a∥c
15.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是 .
答案:153°
16.如图5-2-3是一个长方体,用符号表示下列两棱的位置关系:
图5-2-3
AB________BC;AB________EF;AB________CD.
答案:⊥ ∥ ∥
解答题
17.读下列语句,并画出图形.
P是直线AB外一点,直线CD经过点P且与直线AB平行,直线EF也经过点P且与直线AB垂直.
解:如图所示:
18.完成下面的推理过程:
如图,CB平分∠ACD,∠1=∠3.试说明:AB∥CD.
解:∵CB平分∠ACD,
∴∠1=∠2(角平分线的定义).
∵∠1=∠3,
∴∠2=∠3.
∴AB∥CD(内错角相等,两直线平行).
19.如图5-2-15,PE⊥MN,QF⊥MN,∠1=∠2,直线AB与CD平行吗?为什么?
图5-2-15
解:AB∥CD.理由如下:
∵PE⊥MN,QF⊥MN(已知),
∴∠MEP=∠MFQ=90°(垂直的定义).
又∵∠1=∠2(已知),
∴∠MEP-∠1=∠MFQ-∠2(等式的性质),
即∠MEB=∠MFD,
∴AB∥CD(同位角相等,两直线平行).
20.如图,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明:AB∥CD.
解:∵OF平分∠EOD,∠FOD=25°,
∴∠EOD=2∠FOD=50°.
又∵∠OEB=130°,
∴∠OEB+∠EOD=180°.
∴AB∥CD(同旁内角互补,两直线平行).
21.如图5-2-9,P是线段AB的中点,过点P画BC的平行线交AC于点Q,再过点Q画AB的平行线交BC于点S.
(1)用刻度尺测量后确定AQ与QC,CS与BS的数量关系;
(2)用刻度尺测量后确定PQ与BC,QS与AB的数量关系,你发现了什么?用简洁的语言把你发现的规律叙述出来.
图5-2-9
解:所画图形如图所示.
(1)经测量得到AQ=QC,
CS=BS.
(2)经测量得到PQ=BC,QS=AB.
22.经过三角形一边的中点,画另一边的平行线,则这条平行线平分第三边;三角形两边中点之间线段的长度等于第三边长度的一半.
如图,要判定AB∥CD,需要哪些条件?根据是什么?
解:①若考虑截线AD,则需∠D+∠DAB=180°,根据是同旁内角互补,两直线平行.
②若考虑截线AE,则需∠CEA+∠EAB=180°,根据是同旁内角互补,两直线平行或∠DEA=∠EAB,根据是内错角相等,两直线平行.
③若考虑截线AC,则需∠DCA=∠CAB,根据是内错角相等,两直线平行.
④若考虑截线FC,则需∠DCF+∠AFC=180°,根据是同旁内角互补,两直线平行或∠DCF=∠BFC,根据是内错角相等,两直线平行.
⑤若考虑截线BC,则需∠DCB+∠B=180°,根据是同旁内角互补,两直线平行.
23.小明到工厂进行社会实践活动时,发现工人师傅生产了一种如图5-2-23所示的零件,要求AB∥CD,∠BAE=35°,∠AED=90°.小明发现工人师傅只是量出∠BAE=35°,∠AED=90°后,又量了∠EDC=55°,就说AB与CD肯定是平行的.你知道原因吗?
图5-2-23
解:以E为顶点,AE为一边,在∠AED的内部作∠AEM=∠BAE=35°,∴AB∥EM(内错角相等,两直线平行).
又∵∠AED=90°,∴∠DEM=∠EDC=55°,
∴CD∥EM(内错角相等,两直线平行),
∴AB∥CD(平行于同一条直线的两直线平行).
