高中数学第二章推理与证明2.3.1数学归纳法课件 新人教B版选修2_2(26张PPT)
文档属性
| 名称 | 高中数学第二章推理与证明2.3.1数学归纳法课件 新人教B版选修2_2(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-04 09:07:57 | ||
图片预览






文档简介
课件26张PPT。2.3
数学归纳法1、已知数列{ an }的通项公式为
分别计算a1、a2、a3、a4、的值,猜想an3、三角形的内角和为180°,四边形的内角和为2?180°,五 边形的内角和为3?180°,于是有:凸n边形的内角和为 Sn= (n- 2) ? 180°。
如何通过有限个步骤的推理,证明n取所有正整数都成立?问题引入数学归纳法对于某些与 有关的命题常常采用下面的方法来证明它的正确性:先证明当n取第一个值n0时命题成立;2. 当n=k(k?N*,k≥n0)时命题成立, 当n=k+1时命题也成立。
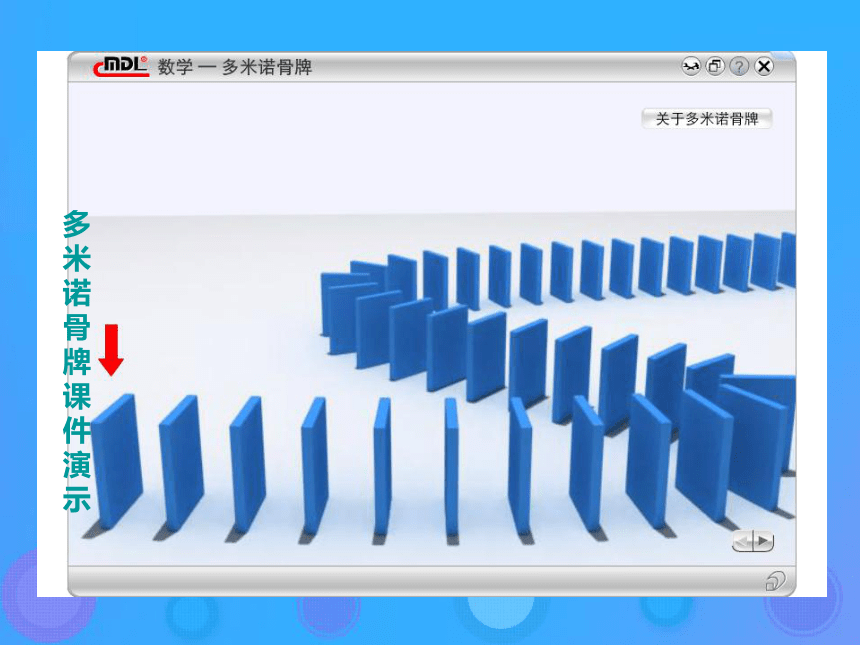
这种证明方法就叫做 。数学归纳法正整数n假设证明 多
米
诺
骨
牌
课
件
演
示 例1:用数学归纳法证明:
1×2+2×3+3×4+…+n(n+1) = 从n=k到n=k+1有什么变化利用假设凑结论证明:2)假设n=k时命题成立,即
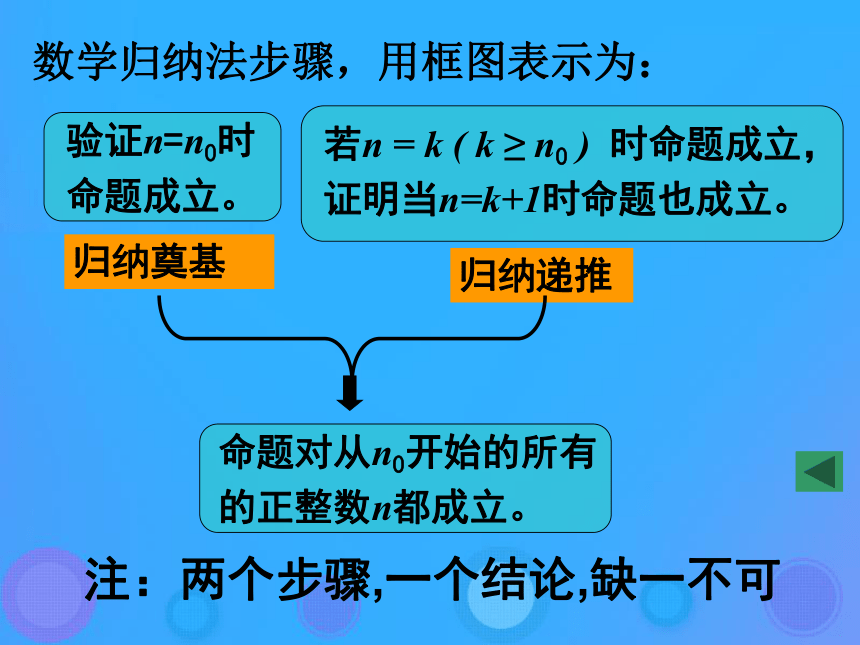
1×2+2×3+3×4+…+k(k+1)==∴ n=k+1时命题正确。 由(1)和(2)知,当 ,命题正确。1)当n=1时,左边=1×2=2,右边= =2. 命题成立数学归纳法步骤,用框图表示为: 归纳奠基归纳递推 注:两个步骤,一个结论,缺一不可上如证明对吗?为什么?证明:①当n=1时,左边=②设n=k时,有即n=k+1时,命题成立。
根据①②问可知,对n∈N*,等式成立。思考:用数学归纳法证明:当第二步证明中没有用到假设,这不是数学归纳法证明。则,当n=k+1时1+3+5+‥+(2n-1)=正确解法:用数学归纳法证明n2 即当n=k+1时等式也成立。根据(1)和(2)可知,等式对任何 都成立。证明:1+3+5+‥+(2k-1)+[2(k+1)-1]那么当n=k+1时(2)假设当n=k时,等式成立,即(1)当n=1时,左边=1,右边=1,等式成立。(假设)(利用假设)注意:递推基础不可少,
归纳假设要用到,
结论写明莫忘掉。(凑结论)用数学归纳法证明恒等式的步骤及注意事项:① 明确首取值n0并验证真假。(必不可少)
② “假设n=k时命题正确”并写出命题形式。
③ 分析“n=k+1时”命题是什么,并找出与“n=k”时
命题形式的差别。弄清左端应增加的项。
④ 明确等式左端变形目标,掌握恒等式变形常用的
方法:乘法公式、因式分解、添拆项、配方等,
并 用上假设。课堂练习2、求证:1+2+3+…+n=
n(n+1 )课堂小结1、数学归纳法能够解决哪一类问题?
一般被应用于证明某些与正整数有关的数学命题
2、数学归纳法证明命题的步骤是什么?
两个步骤和一个结论,缺一不可
3、数学归纳法证明命题的关键在哪里?
关键在第二步,即归纳假设要用到,解题目标要明确
4、数学归纳法体现的核心思想是什么?
递推思想,运用“有限”的手段,来解决“无限”的问题
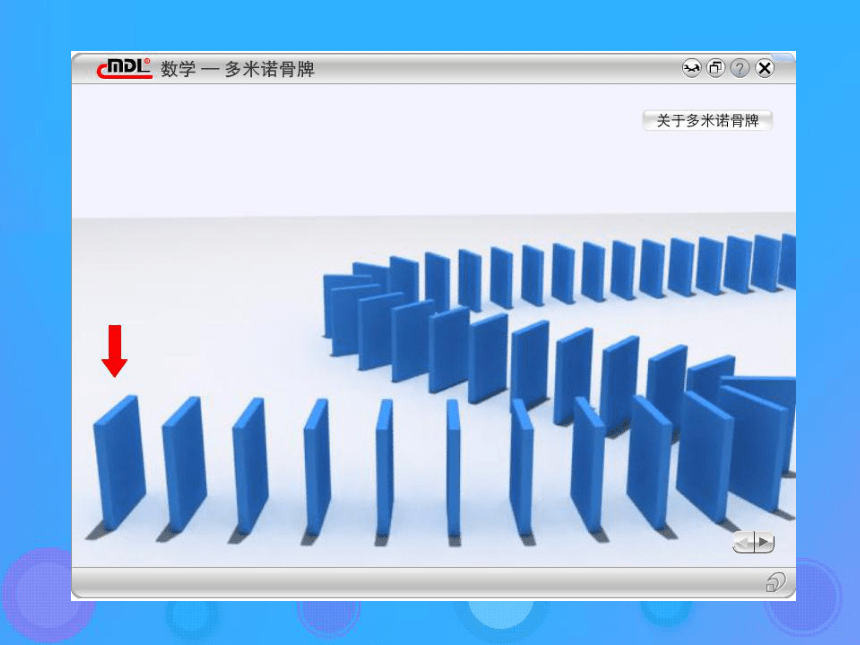
注意类比思想的运用作业:求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)谢谢大家再见多米诺骨牌游戏的原理 这个猜想的证明方法(1)第一块骨牌倒下。(2)若第k块倒下时,则相邻的第k+1块也倒下。根据(1)和 (2),
可知不论有多少块骨牌,都能全部倒下。(1)当n=1时猜想成立。(2)若当n=k时猜想成立,
即 ,则当n=k+1时猜想
也成立,即 。根据(1)和(2),可知对任意的正整数n,猜想 都成立。已知数列从前,有个小孩叫万百千,他开始上学识字。第一天先生教他个“一”字。第二天先生又教了个“二”字。第三天,他想先生一定是教“三”字了,并预先在纸上划了三横。果然这天教了个“三”字。于是他得了一个结论:“四”一定是四横,“五”一定是五横,以此类推,…从此,他不再去上学,家长发现问他为何不去上学,他自豪地说:“我都会了”。家长要他写出自己的名字,“万百千”写名字结果可想而知。” "万百千"的笑话费尔马(1601.8—1665.1),法国数学家。 (费马猜想)结论是错误的。例4.求证:凸n边形的对角线的条数为证明:(1)当n=4时,四边形的对角线有2条,f(4)=2,所以对于n=2,命题成立.(2)设凸k边形的对角线的条数为当n=k+1时,k+1边形比k边形多了一个顶点,解:猜想: 如何通过有限个步骤的推理,证明n取所有正整数都成立?证明2、对于数列{ },已知 , 求出数列前4项,你能得到什么猜想?根据(1)(2)可知对任意正整数n猜想都成立.证明:练习:1、如果{an}是一个等差数列,
则an=a1+(n-1)d对于一切n∈N*都成立。 证明:(1)当n=1时,左边=a1,右边=a1 +(1-1)d=a1,
∴ 当n=1时,结论成立
(2)假设当n=k时结论成立,即ak=a1+(k-1)d ∴当n=k+1时,结论也成立.由(1)和(2)知,等式对于任何n∈N*都成立。利用假设注意 1.用数学归纳法进行证明时,要分两个步骤,两个步骤缺一不可.2(1)(归纳奠基)是递推的基础. 找准n0(2)(归纳递推)是递推的依据 n=k时命题成立.作为必用的条件运用,而n=k+1时情况则有待利用假设及已知的定义、公式、定理等加以证明证明:(1)当n=1时,左边=1,右边=1,等式成立;(2)假设当n=k时,等式成立,即那么 这就是说,当n=k+1时,等式也成立,
由(1)和(2)可以断定,等式对任何n∈N+都成立。
分别计算a1、a2、a3、a4、的值,猜想an3、三角形的内角和为180°,四边形的内角和为2?180°,五 边形的内角和为3?180°,于是有:凸n边形的内角和为 Sn= (n- 2) ? 180°。
如何通过有限个步骤的推理,证明n取所有正整数都成立?问题引入数学归纳法对于某些与 有关的命题常常采用下面的方法来证明它的正确性:先证明当n取第一个值n0时命题成立;2. 当n=k(k?N*,k≥n0)时命题成立, 当n=k+1时命题也成立。
这种证明方法就叫做 。数学归纳法正整数n假设证明 多
米
诺
骨
牌
课
件
演
示 例1:用数学归纳法证明:
1×2+2×3+3×4+…+n(n+1) = 从n=k到n=k+1有什么变化利用假设凑结论证明:2)假设n=k时命题成立,即
1×2+2×3+3×4+…+k(k+1)==∴ n=k+1时命题正确。 由(1)和(2)知,当 ,命题正确。1)当n=1时,左边=1×2=2,右边= =2. 命题成立数学归纳法步骤,用框图表示为: 归纳奠基归纳递推 注:两个步骤,一个结论,缺一不可上如证明对吗?为什么?证明:①当n=1时,左边=②设n=k时,有即n=k+1时,命题成立。
根据①②问可知,对n∈N*,等式成立。思考:用数学归纳法证明:当第二步证明中没有用到假设,这不是数学归纳法证明。则,当n=k+1时1+3+5+‥+(2n-1)=正确解法:用数学归纳法证明n2 即当n=k+1时等式也成立。根据(1)和(2)可知,等式对任何 都成立。证明:1+3+5+‥+(2k-1)+[2(k+1)-1]那么当n=k+1时(2)假设当n=k时,等式成立,即(1)当n=1时,左边=1,右边=1,等式成立。(假设)(利用假设)注意:递推基础不可少,
归纳假设要用到,
结论写明莫忘掉。(凑结论)用数学归纳法证明恒等式的步骤及注意事项:① 明确首取值n0并验证真假。(必不可少)
② “假设n=k时命题正确”并写出命题形式。
③ 分析“n=k+1时”命题是什么,并找出与“n=k”时
命题形式的差别。弄清左端应增加的项。
④ 明确等式左端变形目标,掌握恒等式变形常用的
方法:乘法公式、因式分解、添拆项、配方等,
并 用上假设。课堂练习2、求证:1+2+3+…+n=
n(n+1 )课堂小结1、数学归纳法能够解决哪一类问题?
一般被应用于证明某些与正整数有关的数学命题
2、数学归纳法证明命题的步骤是什么?
两个步骤和一个结论,缺一不可
3、数学归纳法证明命题的关键在哪里?
关键在第二步,即归纳假设要用到,解题目标要明确
4、数学归纳法体现的核心思想是什么?
递推思想,运用“有限”的手段,来解决“无限”的问题
注意类比思想的运用作业:求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)谢谢大家再见多米诺骨牌游戏的原理 这个猜想的证明方法(1)第一块骨牌倒下。(2)若第k块倒下时,则相邻的第k+1块也倒下。根据(1)和 (2),
可知不论有多少块骨牌,都能全部倒下。(1)当n=1时猜想成立。(2)若当n=k时猜想成立,
即 ,则当n=k+1时猜想
也成立,即 。根据(1)和(2),可知对任意的正整数n,猜想 都成立。已知数列从前,有个小孩叫万百千,他开始上学识字。第一天先生教他个“一”字。第二天先生又教了个“二”字。第三天,他想先生一定是教“三”字了,并预先在纸上划了三横。果然这天教了个“三”字。于是他得了一个结论:“四”一定是四横,“五”一定是五横,以此类推,…从此,他不再去上学,家长发现问他为何不去上学,他自豪地说:“我都会了”。家长要他写出自己的名字,“万百千”写名字结果可想而知。” "万百千"的笑话费尔马(1601.8—1665.1),法国数学家。 (费马猜想)结论是错误的。例4.求证:凸n边形的对角线的条数为证明:(1)当n=4时,四边形的对角线有2条,f(4)=2,所以对于n=2,命题成立.(2)设凸k边形的对角线的条数为当n=k+1时,k+1边形比k边形多了一个顶点,解:猜想: 如何通过有限个步骤的推理,证明n取所有正整数都成立?证明2、对于数列{ },已知 , 求出数列前4项,你能得到什么猜想?根据(1)(2)可知对任意正整数n猜想都成立.证明:练习:1、如果{an}是一个等差数列,
则an=a1+(n-1)d对于一切n∈N*都成立。 证明:(1)当n=1时,左边=a1,右边=a1 +(1-1)d=a1,
∴ 当n=1时,结论成立
(2)假设当n=k时结论成立,即ak=a1+(k-1)d ∴当n=k+1时,结论也成立.由(1)和(2)知,等式对于任何n∈N*都成立。利用假设注意 1.用数学归纳法进行证明时,要分两个步骤,两个步骤缺一不可.2(1)(归纳奠基)是递推的基础. 找准n0(2)(归纳递推)是递推的依据 n=k时命题成立.作为必用的条件运用,而n=k+1时情况则有待利用假设及已知的定义、公式、定理等加以证明证明:(1)当n=1时,左边=1,右边=1,等式成立;(2)假设当n=k时,等式成立,即那么 这就是说,当n=k+1时,等式也成立,
由(1)和(2)可以断定,等式对任何n∈N+都成立。
