高中数学第一章导数及其应用1.3.1利用导数判断函数的单调性课件 新人教B版选修2_2(18张PPT)
文档属性
| 名称 | 高中数学第一章导数及其应用1.3.1利用导数判断函数的单调性课件 新人教B版选修2_2(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 747.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 09:42:12 | ||
图片预览






文档简介
课件18张PPT。1.3.1利用导数判断函数的单调性 数学是研究现实世界中数量关系和空间形式的科学。简单地说,就是研究数和形的科学。学习目标重点、难点(2)会利用导数判断函数的单调性并求函数的单调区间(1)探索函数的单调性与导数的关系重点:利用导数研究函数的单调性,会求函数的单调区间难点:探究函数的单调性与导数的关系,如何用导数判断函数的单调性复习引入问题1.函数单调性的定义是什么?问题2:用定义法判断函数单调性的步骤:(1)在给定区间内任取x1(2)作差f(x1)-f(x2);
(3)变形;
(4)判断符号;
(5)下结论。1.3.1 函数的单调性与导数 (1)自主探究,大胆猜想
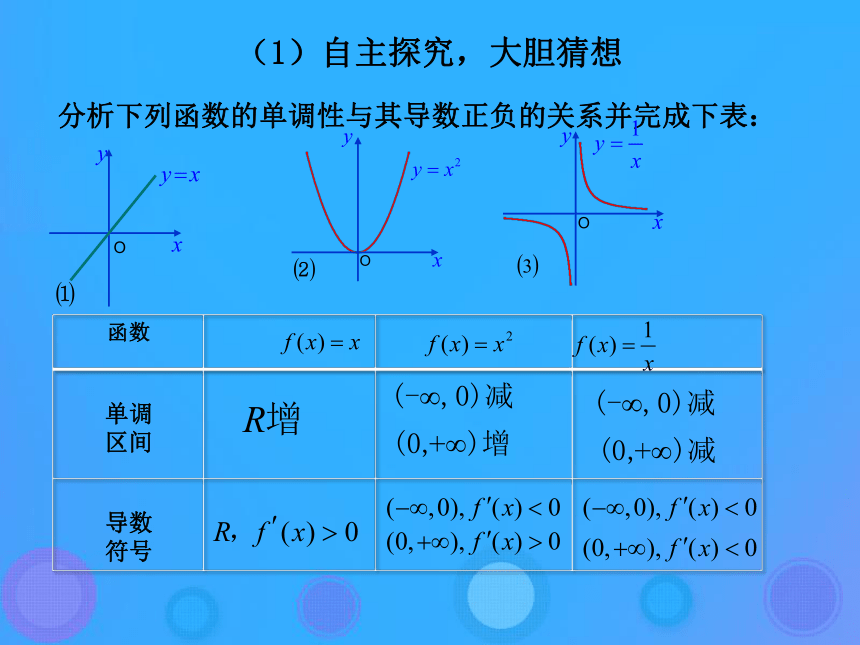
分析下列函数的单调性与其导数正负的关系并完成下表:
1. 函数单调性与其导数正负的关系:例1 判断下列函数的单调性, 并求出单调区间:, 2、你能小结求解函数单调区间的步骤吗?例1 判断下列函数的单调性, 并求出单调区间:单调递减例2 已知导函数 f’(x)的下列信息:当1 < x < 4 时, f’(x)>0当 x > 4 , 或 x < 1时, f’(x)<0
当 x = 4 , 或 x = 1时, f’(x)=0
试画出函数 f(x)的图象的大致形状.解: 当1 < x < 4 时, f’(x)>0可知 f(x)在此区间内单调递增; 当 x > 4 , 或 x < 1时, f’(x)<0可知 f(x) 在此区间内单调递减; 当 x = 4 , 或 x = 1时,
f’(x)=0
综上, 函数f(x) 图象的大致形状如右图所示.2.求可导函数f(x)单调区间的步骤:课堂小结1. 函数单调性与其导数正负的关系:布置作业
(3)变形;
(4)判断符号;
(5)下结论。1.3.1 函数的单调性与导数 (1)自主探究,大胆猜想
分析下列函数的单调性与其导数正负的关系并完成下表:
1. 函数单调性与其导数正负的关系:例1 判断下列函数的单调性, 并求出单调区间:, 2、你能小结求解函数单调区间的步骤吗?例1 判断下列函数的单调性, 并求出单调区间:单调递减例2 已知导函数 f’(x)的下列信息:当1 < x < 4 时, f’(x)>0当 x > 4 , 或 x < 1时, f’(x)<0
当 x = 4 , 或 x = 1时, f’(x)=0
试画出函数 f(x)的图象的大致形状.解: 当1 < x < 4 时, f’(x)>0可知 f(x)在此区间内单调递增; 当 x > 4 , 或 x < 1时, f’(x)<0可知 f(x) 在此区间内单调递减; 当 x = 4 , 或 x = 1时,
f’(x)=0
综上, 函数f(x) 图象的大致形状如右图所示.2.求可导函数f(x)单调区间的步骤:课堂小结1. 函数单调性与其导数正负的关系:布置作业
