高中数学第一章导数及其应用1.3.2利用导数研究函数极值课件 新人教B版选修2_2(32张PPT)
文档属性
| 名称 | 高中数学第一章导数及其应用1.3.2利用导数研究函数极值课件 新人教B版选修2_2(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 867.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-03 00:00:00 | ||
图片预览








文档简介
课件32张PPT。1.3.2利用导数
研究函数的极值问题1、用导数法确定函数的单调性的步骤是1、确定函数f(x)的定义域
2、求出导函数
3、解不等式 ,得函数f(x)的单调增区间
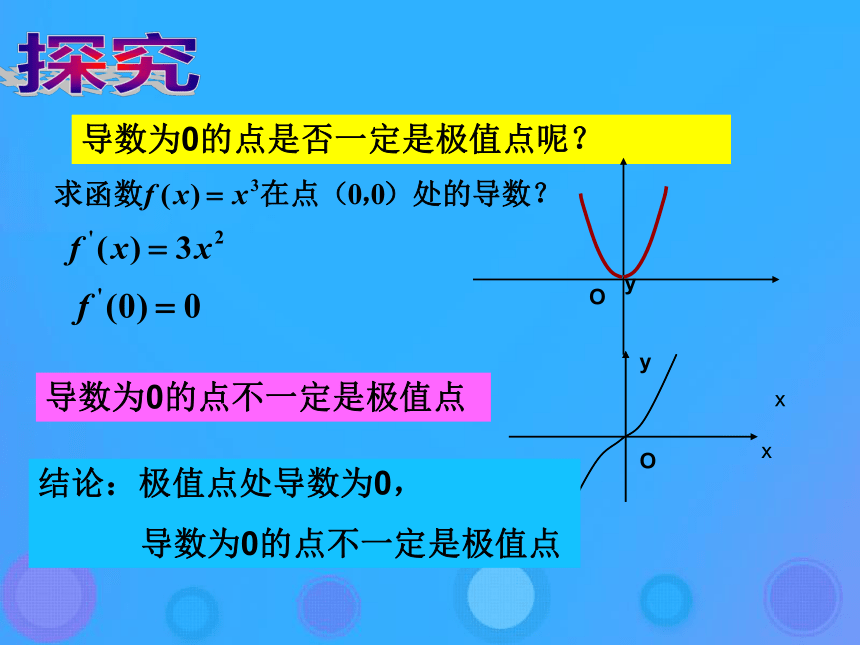
解不等式 ,得函数f(x)的单调减区间xyo导数为0的点是否一定是极值点呢?导数为0的点不一定是极值点探究结论:极值点处导数为0,
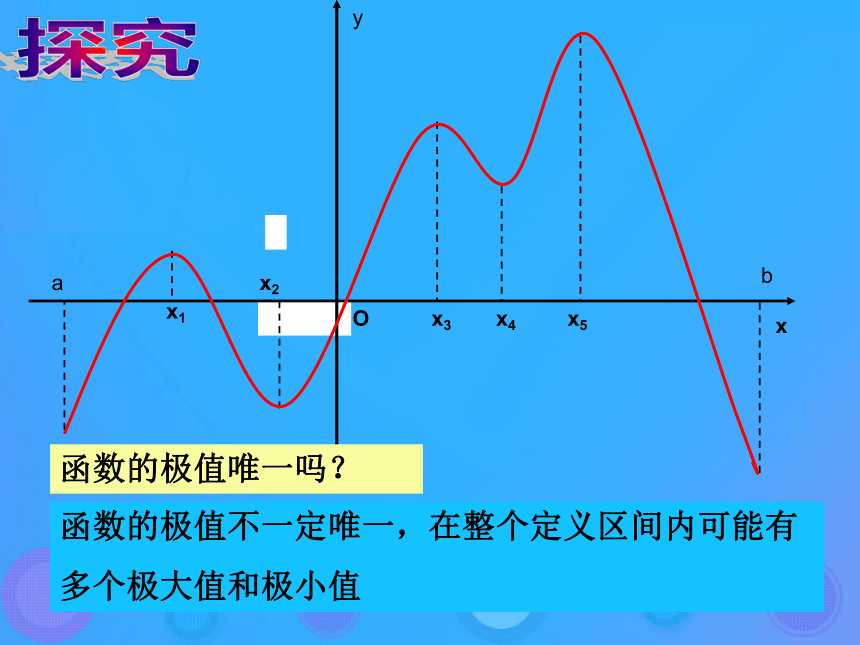
导数为0的点不一定是极值点yyyyyyyxOyabx1x2x3x4x5xOyabx1x2x3x4x5函数的极值唯一吗?探究函数的极值不一定唯一,在整个定义区间内可能有
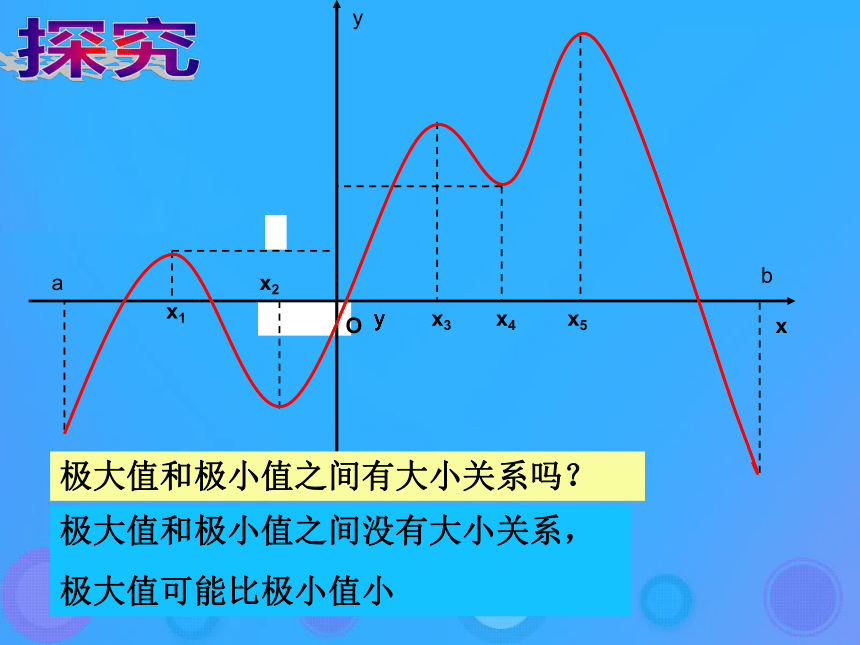
多个极大值和极小值yyyyyyyxOyabx1x2x3x4x5极大值和极小值之间有大小关系吗?探究极大值和极小值之间没有大小关系,
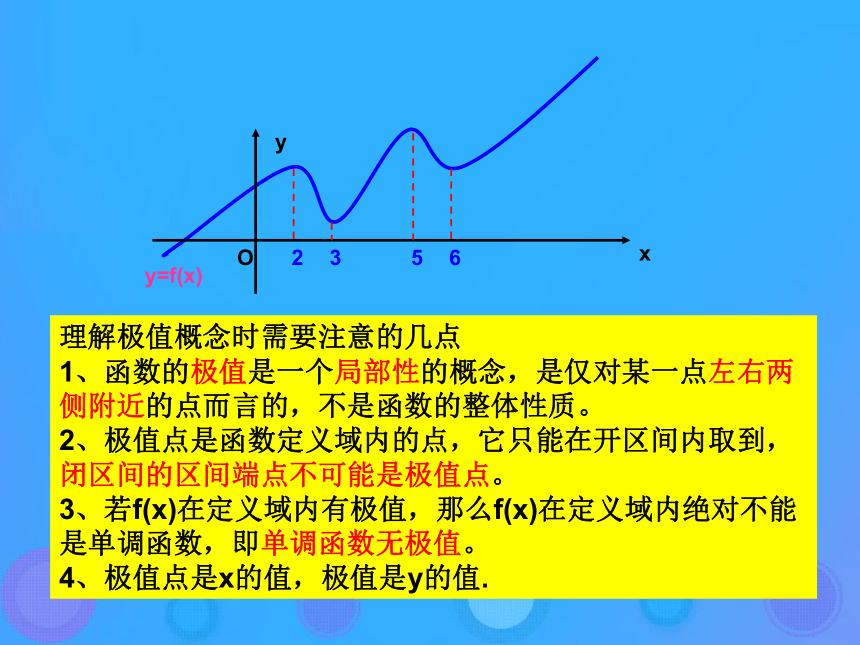
极大值可能比极小值小理解极值概念时需要注意的几点
1、函数的极值是一个局部性的概念,是仅对某一点左右两侧附近的点而言的,不是函数的整体性质。
2、极值点是函数定义域内的点,它只能在开区间内取到,闭区间的区间端点不可能是极值点。
3、若f(x)在定义域内有极值,那么f(x)在定义域内绝对不能是单调函数,即单调函数无极值。
4、极值点是x的值,极值是y的值.1.求极值
2.求端点值f(a),f(b)
3.比较极值和端点值的大小,求出最值今天,我们学习了函数的极值的概念,并学习了利用导数求极值的方法三、通过本节课,充分体会数形结合思想在数学中的应用。课堂小结1.求极值
2.求端点值f(a),f(b)
3.比较极值和端点值的大小,求出最值1、判断下面4个命题,其中真命题的序号为
(1)可导函数必有极值
(2)函数的极值点必在定义域内
(3)函数的极小值一定小于极大值
(设极小值、极大值都存在)
(4)函数的极小值(或极大值)不会多于一个牛刀小试:(2)探究一下极值点两侧导数值的正负变化情况极大值点左侧导数为 ,正探究右侧导数为 负结论牛刀小试:CA牛刀小试:牛刀小试:解已知函数y=f(x),设x0是定义域(a,b)内
任意一点,如果在x0附近的所有x,都有f(x)记作:y极大=f(x0),
并把x0称为函数f(x)的一个极大值点。极大值和极小值统称为极值,极大值点、极小值点统称极值点.如果在x0附近的所有x,都有f(x)>f(x0),则称函数f(x)在点x0处取极小值。
记作:y极小=f(x0),
并把x0称为函数f(x)的一个极小值点。自变量x的值原函数值yyyyyyyyxOyabx1x2x3x4x5结论:
设x=x0是y=f(x)的极值点,且f(x)在x=x0是可导的,则必有f ’ (x0)=0在极值点处,如果曲线有切线,则切线有什么特点?探究极值点处的切线是水平的这个特点反映在导数上,能说明什么?极值点处的导数是0探究一下极值点两侧导数值的正负变化情况极小值点左侧导数为 ,右侧导数为 正负探究a=6C利用导数求极值:例1:(3)图像信息问题:
例2:
研究函数的极值问题1、用导数法确定函数的单调性的步骤是1、确定函数f(x)的定义域
2、求出导函数
3、解不等式 ,得函数f(x)的单调增区间
解不等式 ,得函数f(x)的单调减区间xyo导数为0的点是否一定是极值点呢?导数为0的点不一定是极值点探究结论:极值点处导数为0,
导数为0的点不一定是极值点yyyyyyyxOyabx1x2x3x4x5xOyabx1x2x3x4x5函数的极值唯一吗?探究函数的极值不一定唯一,在整个定义区间内可能有
多个极大值和极小值yyyyyyyxOyabx1x2x3x4x5极大值和极小值之间有大小关系吗?探究极大值和极小值之间没有大小关系,
极大值可能比极小值小理解极值概念时需要注意的几点
1、函数的极值是一个局部性的概念,是仅对某一点左右两侧附近的点而言的,不是函数的整体性质。
2、极值点是函数定义域内的点,它只能在开区间内取到,闭区间的区间端点不可能是极值点。
3、若f(x)在定义域内有极值,那么f(x)在定义域内绝对不能是单调函数,即单调函数无极值。
4、极值点是x的值,极值是y的值.1.求极值
2.求端点值f(a),f(b)
3.比较极值和端点值的大小,求出最值今天,我们学习了函数的极值的概念,并学习了利用导数求极值的方法三、通过本节课,充分体会数形结合思想在数学中的应用。课堂小结1.求极值
2.求端点值f(a),f(b)
3.比较极值和端点值的大小,求出最值1、判断下面4个命题,其中真命题的序号为
(1)可导函数必有极值
(2)函数的极值点必在定义域内
(3)函数的极小值一定小于极大值
(设极小值、极大值都存在)
(4)函数的极小值(或极大值)不会多于一个牛刀小试:(2)探究一下极值点两侧导数值的正负变化情况极大值点左侧导数为 ,正探究右侧导数为 负结论牛刀小试:CA牛刀小试:牛刀小试:解已知函数y=f(x),设x0是定义域(a,b)内
任意一点,如果在x0附近的所有x,都有f(x)
并把x0称为函数f(x)的一个极大值点。极大值和极小值统称为极值,极大值点、极小值点统称极值点.如果在x0附近的所有x,都有f(x)>f(x0),则称函数f(x)在点x0处取极小值。
记作:y极小=f(x0),
并把x0称为函数f(x)的一个极小值点。自变量x的值原函数值yyyyyyyyxOyabx1x2x3x4x5结论:
设x=x0是y=f(x)的极值点,且f(x)在x=x0是可导的,则必有f ’ (x0)=0在极值点处,如果曲线有切线,则切线有什么特点?探究极值点处的切线是水平的这个特点反映在导数上,能说明什么?极值点处的导数是0探究一下极值点两侧导数值的正负变化情况极小值点左侧导数为 ,右侧导数为 正负探究a=6C利用导数求极值:例1:(3)图像信息问题:
例2:
