冀教版八年级数学下册 第二十二章 四边形单元测试(word版有答案)
文档属性
| 名称 | 冀教版八年级数学下册 第二十二章 四边形单元测试(word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 103.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-03 15:04:44 | ||
图片预览

文档简介
冀教版八年级数学下册 第二十二章 四边形单元测试
(word版有答案)
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共36分)
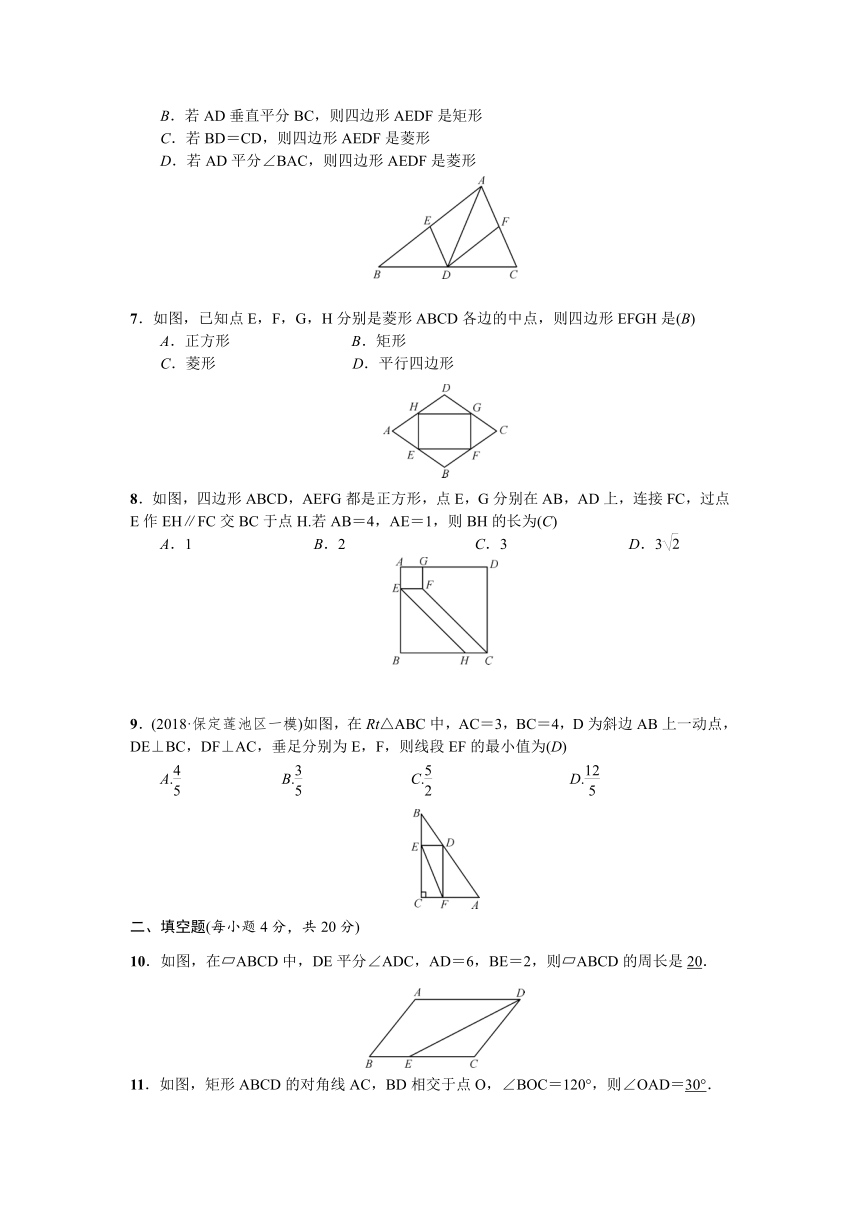
1.如图,在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,则CD的长是(C)
A.20 B.10 C.5 D.
2.如图,在?ABCD中,AC与BD相交于点O,则下列结论不一定成立的是(D)
A.BO=DO B.∠BAD=∠BCD
C.CD=AB D.AC=BD
3.矩形具有而一般的平行四边形不一定具有的特征是(B)
A.对角相等 B.对角线相等
C.对角线互相平分 D.对边相等
4.如图,把一张矩形纸片沿着EF折叠,点C,D分别落在M,N的位置,且∠MFB=∠MFE.则∠AEF=(D)
A.30° B.36° C.45° D.72°
5.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为(A)
A.2 B. C.6 D.8
6.如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是(D)
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
7.如图,已知点E,F,G,H分别是菱形ABCD各边的中点,则四边形EFGH是(B)
A.正方形 B.矩形
C.菱形 D.平行四边形
8.如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为(C)
A.1 B.2 C.3 D.3
9.(2018·保定莲池区一模)如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E,F,则线段EF的最小值为(D)
A. B. C. D.
二、填空题(每小题4分,共20分)
10.如图,在?ABCD中,DE平分∠ADC,AD=6,BE=2,则?ABCD的周长是20.
11.如图,矩形ABCD的对角线AC,BD相交于点O,∠BOC=120°,则∠OAD=30°.
12.正方形ABCD的边长为8,点E为正方形边上一点,连接BE,且BE=10,则AE的长为6或2.
13.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为(+1,1).
14.如图,在等边△ABC中,BC=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.如果点E,F同时出发,设运动时间为t(s),当t=2或6s时,以A,C,E,F为顶点四边形是平行四边形.
三、解答题(共44分)
15.(10分)如图,在ABCD中,AE=CF,M,N分别是BE,DF的中点,求证:四边形MFNE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC且AD∥BC.
∵AE=CF,
∴DE=BF,且DE∥BF.
∴四边形BEDF是平行四边形.
∴BE=DF.
∵M,N分别是BE,DF的中点,
∴ME=NF,且ME∥NF.
∴四边形MFNE是平行四边形.
16.(10分)如图,在ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.∴DF∥BE.
∵CF=AE,∴DF=BE.
∴四边形BFDE是平行四边形.
∵DE⊥AB,∴∠DEB=90°.
∴四边形BFDE是矩形.
(2)∵AB∥CD,∴∠BAF=∠AFD.
∵AF平分∠BAD,∴∠DAF=∠AFD.
∴AD=DF.
在Rt△ADE中,∵AE=3,DE=4,
∴AD==5.
∴矩形BFDE的面积为20.
17.(12分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
解:(1)证明:连接DF,∵E为AD的中点,
∴AE=DE.
∵AF∥BC,
∴∠AFE=∠DBE.
在△AFE和△DBE中,
∴△AFE≌△DBE(AAS).∴EF=BE.
∵AE=DE,∴四边形AFDB是平行四边形.
∴BD=AF.
∵AD为中线,∴DC=BD.∴AF=DC.
(2)四边形ADCF的形状是菱形,证明如下:
∵AF=DC,AF∥BC,
∴四边形ADCF是平行四边形.
∵AC⊥AB,∴∠CAB=90°.
∵AD为中线,∴AD=BC=DC.
∴平行四边形ADCF是菱形.
18.(12分)如图1,正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.
(1)求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
解:(1)证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE.
∴∠MEA=∠AFO.
在△BOE和△AOF中,
∴△BOE≌△AOF(AAS).
∴OE=OF.
(2)OE=OF成立.
证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,∠E+∠OBE=90°.
又∵∠MBF=∠OBE,∴∠F=∠E.
在△BOE和△AOF中,
∴△BOE≌△AOF(AAS).
∴OE=OF.
(word版有答案)
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共36分)
1.如图,在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,则CD的长是(C)
A.20 B.10 C.5 D.
2.如图,在?ABCD中,AC与BD相交于点O,则下列结论不一定成立的是(D)
A.BO=DO B.∠BAD=∠BCD
C.CD=AB D.AC=BD
3.矩形具有而一般的平行四边形不一定具有的特征是(B)
A.对角相等 B.对角线相等
C.对角线互相平分 D.对边相等
4.如图,把一张矩形纸片沿着EF折叠,点C,D分别落在M,N的位置,且∠MFB=∠MFE.则∠AEF=(D)
A.30° B.36° C.45° D.72°
5.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为(A)
A.2 B. C.6 D.8
6.如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是(D)
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
7.如图,已知点E,F,G,H分别是菱形ABCD各边的中点,则四边形EFGH是(B)
A.正方形 B.矩形
C.菱形 D.平行四边形
8.如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为(C)
A.1 B.2 C.3 D.3
9.(2018·保定莲池区一模)如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E,F,则线段EF的最小值为(D)
A. B. C. D.
二、填空题(每小题4分,共20分)
10.如图,在?ABCD中,DE平分∠ADC,AD=6,BE=2,则?ABCD的周长是20.
11.如图,矩形ABCD的对角线AC,BD相交于点O,∠BOC=120°,则∠OAD=30°.
12.正方形ABCD的边长为8,点E为正方形边上一点,连接BE,且BE=10,则AE的长为6或2.
13.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为(+1,1).
14.如图,在等边△ABC中,BC=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.如果点E,F同时出发,设运动时间为t(s),当t=2或6s时,以A,C,E,F为顶点四边形是平行四边形.
三、解答题(共44分)
15.(10分)如图,在ABCD中,AE=CF,M,N分别是BE,DF的中点,求证:四边形MFNE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC且AD∥BC.
∵AE=CF,
∴DE=BF,且DE∥BF.
∴四边形BEDF是平行四边形.
∴BE=DF.
∵M,N分别是BE,DF的中点,
∴ME=NF,且ME∥NF.
∴四边形MFNE是平行四边形.
16.(10分)如图,在ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.∴DF∥BE.
∵CF=AE,∴DF=BE.
∴四边形BFDE是平行四边形.
∵DE⊥AB,∴∠DEB=90°.
∴四边形BFDE是矩形.
(2)∵AB∥CD,∴∠BAF=∠AFD.
∵AF平分∠BAD,∴∠DAF=∠AFD.
∴AD=DF.
在Rt△ADE中,∵AE=3,DE=4,
∴AD==5.
∴矩形BFDE的面积为20.
17.(12分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
解:(1)证明:连接DF,∵E为AD的中点,
∴AE=DE.
∵AF∥BC,
∴∠AFE=∠DBE.
在△AFE和△DBE中,
∴△AFE≌△DBE(AAS).∴EF=BE.
∵AE=DE,∴四边形AFDB是平行四边形.
∴BD=AF.
∵AD为中线,∴DC=BD.∴AF=DC.
(2)四边形ADCF的形状是菱形,证明如下:
∵AF=DC,AF∥BC,
∴四边形ADCF是平行四边形.
∵AC⊥AB,∴∠CAB=90°.
∵AD为中线,∴AD=BC=DC.
∴平行四边形ADCF是菱形.
18.(12分)如图1,正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.
(1)求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
解:(1)证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE.
∴∠MEA=∠AFO.
在△BOE和△AOF中,
∴△BOE≌△AOF(AAS).
∴OE=OF.
(2)OE=OF成立.
证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,∠E+∠OBE=90°.
又∵∠MBF=∠OBE,∴∠F=∠E.
在△BOE和△AOF中,
∴△BOE≌△AOF(AAS).
∴OE=OF.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
