冀教版八年级数学下册 第十九章 平面直角坐标系 课时同步试题(word版有答案)
文档属性
| 名称 | 冀教版八年级数学下册 第十九章 平面直角坐标系 课时同步试题(word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 666.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-03 15:06:48 | ||
图片预览


文档简介
冀教版八年级数学下册 第十九章 平面直角坐标系 课时同步试题
19.1 确定平面上物体的位置
01 基础题
知识点1 用有序实数对表示物体的位置
1.如图,一方队正沿箭头所指的方向前进, A的位置为三列四行,表示为(3,4),那么B 的位置是(A)
A.(4,5) B.(5,4) C.(4,2) D.(4,3)
2.若将7门6楼简记为(7,6),则6门7楼可简记为(6,7),(8,5)表示的意义是8门5楼.
知识点2 用“方位角+距离”表示物体的位置
3.已知古塔在嘉淇的北偏东30°方向,且距离嘉淇2 km,符合条件的示意图是(B)
易错点 忽视点的位置需要用一对数来表示
4.(2018·邢台宁晋县期末)以下描述中,能确定具体位置的是(D)
A.万达电影院2排
B.距薛城高铁站2千米
C.北偏东30 ℃
D.东经106 ℃,北纬31 ℃
02 中档题
5.在一座共8层的商业大厦中,每层的摊位布局基本相同.小明的父亲在6楼的位置如图所示,其位置可以表示为(6,2,3).若小明的母亲在5楼,其摊位也可以用如图表示,则小明母亲的摊位的位置可以表示为(5,4,2).
6.(2017·石家庄长安区期中)如图,线段OB,OC,OA的长度分别是1,2,3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),则C点可表示为(2,75°).
7.(教材P31“观察与思考”变式)如图是某次海战中敌我双方战舰对峙示意图(图中1 cm表示20海里).
(1)在我方潜艇的北偏东40°有哪些目标?要想确定敌方战舰B的位置,还需要什么数据?
(2)距离我方潜艇20海里的敌方战舰有哪几艘?
(3)敌方战舰C和敌方战舰A分别在我方潜艇的什么方向?
(4)要确定每艘敌方战舰的位置,都需要哪些数据?
解:(1)在我方潜艇的北偏东40°有敌方战舰B和小岛;要想确定敌方战舰B的位置,还需要知道敌方战舰B与我方潜艇的距离.
(2)距离我方潜艇20海里的敌方战舰有敌方战舰A和C.
(3)敌方战舰C在我方潜艇的正东方向,敌方战舰A在我方潜艇的正南方向.
(4)要确定每艘敌方战舰的位置,需要知道每艘敌方战舰分别在什么方向,与我方潜艇的距离是多少.
8.(2018·唐山滦南县二模)如图,点A在观测点北偏东30°方向,且与观测点的距离为8 km,将点A的位置记作A(8,30°).用同样的方法将点B、点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在(A)
A.点O1 B.点O2 C.点O3 D.点O4
19.2 平面直角坐标系
第1课时 平面直角坐标系中点的坐标表示
01 基础题
知识点1 用坐标表示点
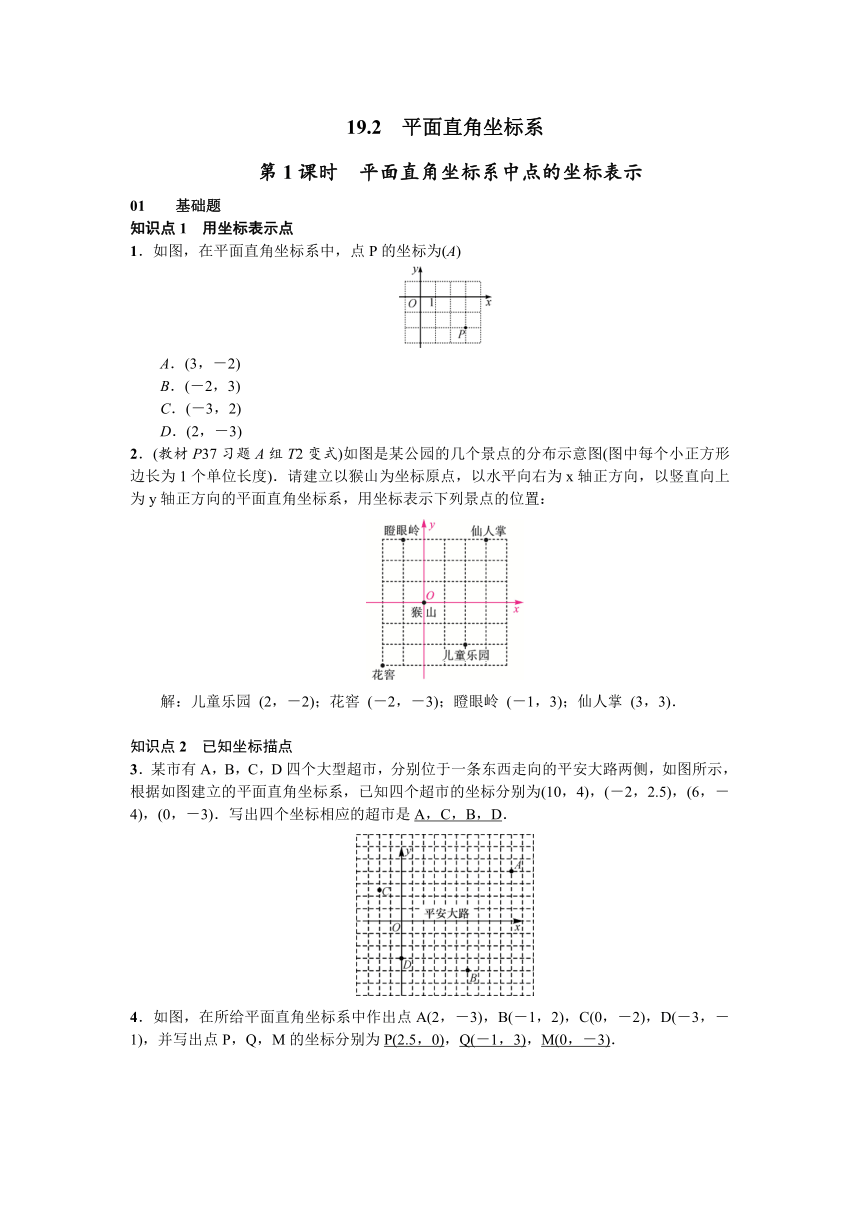
1.如图,在平面直角坐标系中,点P的坐标为(A)
A.(3,-2)
B.(-2,3)
C.(-3,2)
D.(2,-3)
2.(教材P37习题A组T2变式)如图是某公园的几个景点的分布示意图(图中每个小正方形边长为1个单位长度).请建立以猴山为坐标原点,以水平向右为x轴正方向,以竖直向上为y轴正方向的平面直角坐标系,用坐标表示下列景点的位置:
解:儿童乐园 (2,-2);花窖 (-2,-3);瞪眼岭 (-1,3);仙人掌 (3,3).
知识点2 已知坐标描点
3.某市有A,B,C,D四个大型超市,分别位于一条东西走向的平安大路两侧,如图所示,根据如图建立的平面直角坐标系,已知四个超市的坐标分别为(10,4),(-2,2.5),(6,-4),(0,-3).写出四个坐标相应的超市是A,C,B,D.
4.如图,在所给平面直角坐标系中作出点A(2,-3),B(-1,2),C(0,-2),D(-3,-1),并写出点P,Q,M的坐标分别为P(2.5,0),Q(-1,3),M(0,-3).
02 中档题
5.(2017·唐山滦南县期中)平面直角坐标系中x轴的上方有一点P,它到x轴的距离为2,到y轴的距离为3,则点P的坐标为(C)
A.(3,2) B.(-3,2)
C.(3,2)或(-3,2) D.(2,3)
6.(教材P38习题B组T1变式)一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是(A)
A.(30-50,30) B.(30,30-50)
C.(30,30) D.(30,30)
7.若点P(x,y)的坐标满足x+y=xy,则称点P为“和谐点”.请写出一个“和谐点”的坐标:(2,2)或(0,0)(答案不唯一).
8.如图是某公园的平面图(每个方格的边长为100 m).
(1)写出任意五个景点的坐标;
(2)某星期天的上午,苗苗在公园沿(-500,0),(-200,-100),(200,-200),(300,200),(500,0)的路线游玩了半天,请你写出她路上经过的地方.
解:(1)答案不唯一,如:湖心亭(-300,200),望春亭(-200,-100),音乐台(0,400),牡丹园(300,200),游乐园(200,-200).
(2)西门→望春亭→游乐园→牡丹园→东门.
03 综合题
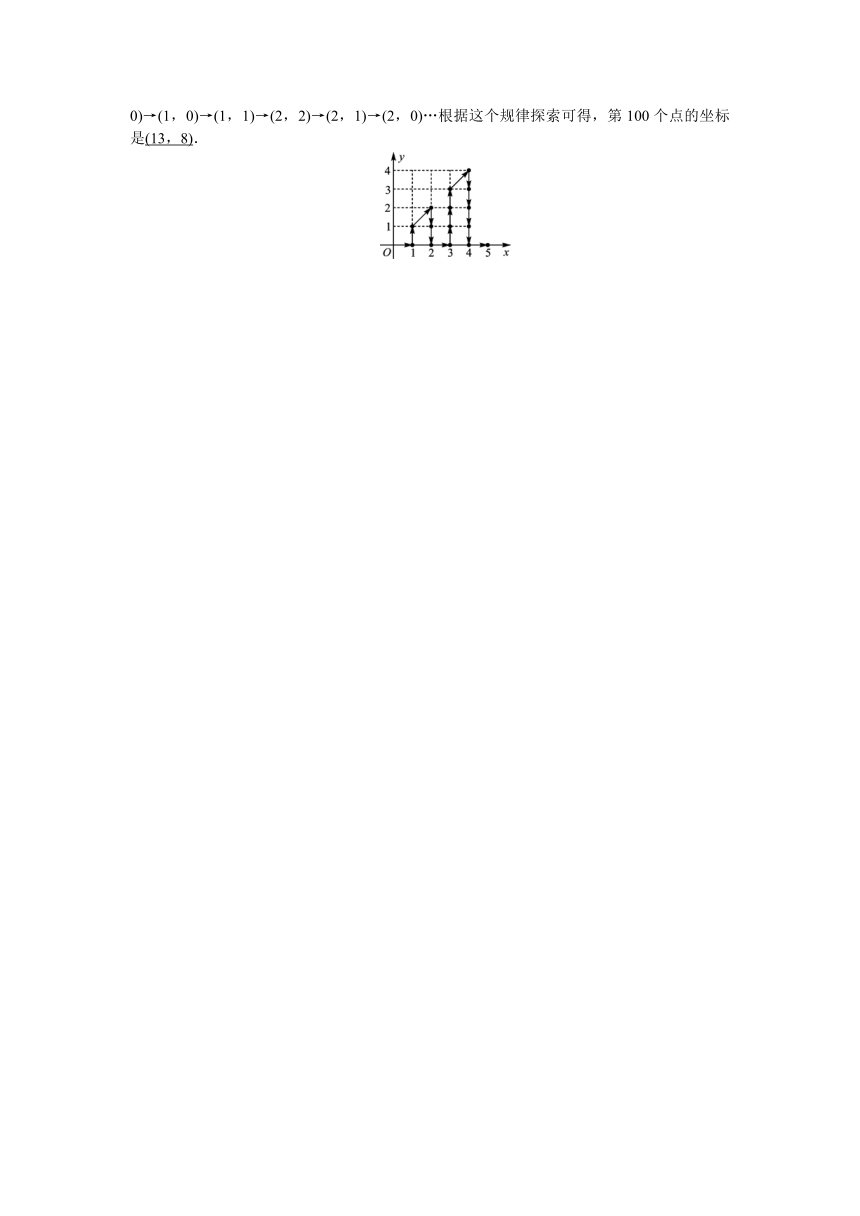
9. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(0,0)→(1,0)→(1,1)→(2,2)→(2,1)→(2,0)…根据这个规律探索可得,第100个点的坐标是(13,8).
第2课时 平面直角坐标系中点的坐标特征
01 基础题
知识点1 坐标平面内点的坐标特征
1.(2017·石家庄长安区期中)在平面直角坐标系中,点(1,5)所在的象限是(A)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.(2018·邢台隆尧县期末)下列各点在第四象限的是(C)
A.(1,2) B.(-1,2)
C.(1,-2) D.(-1,-2)
3.下列各点中,在坐标轴上的是(B)
A.(3,3) B.(-3,0)
C.(-1,2) D.(-2,-3)
4.(2018·扬州)在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是(C)
A.(3,-4) B.(4,-3)
C.(-4,3) D.(-3,4)
5.如图,小手盖住的点的坐标可能为(D)
A.(5,2)
B.(-6,3)
C.(-4,-6)
D.(3,-4)
6.若xy=0,则点P(x,y)一定在(C)
A.x轴上 B.y轴上
C.坐标轴上 D.原点
7.(2018·唐山路北区期末)点P(m+3,m+1)在平面直角坐标系的x轴上,则点P的坐标为(B)
A.(0,-2) B.(2,0)
C.(4,0) D.(0,-4)
8.若点A(x,2)在第二象限,则x的取值范围是x<0.
9.写出一个平面直角坐标系中第三象限内点的坐标:(-2,-1)(答案不唯一).
知识点2 关于x轴(或y轴,或原点)对称的两个点的坐标
10.(2018·武汉)点A(2,-5)关于x轴对称的点的坐标是(A)
A.(2,5) B.(-2,5)
C.(-2,-5) D.(-5,2)
11.(2018·湘潭)如图,点A的坐标为(-1,2),则点A关于y轴的对称点的坐标为(A)
A.(1,2)
B.(-1,-2)
C.(1,-2)
D.(2,-1)
12.(2017·湖州)在平面直角坐标系中,点P(1,2)关于原点的对称点P′的坐标是(D)
A.(1,2) B.(-1,2)
C.(1,-2) D.(-1,-2)
13.小明将某点关于x轴的对称点误认为是关于y轴的对称点,得到点(-2,-3),求该点坐标及其关于x轴、原点的对称点的坐标.
解:因为小明将所求点误认为是关于y轴的对称点而得到点(-2,-3),因此可得该点坐标是(2,-3).所以该点关于x轴的对称点的坐标为(2,3),关于原点的对称点的坐标为(-2,3).
知识点3 平行(或垂直)于坐标轴的直线上点的坐标
14.(教材P40习题B组T2变式)平行于y轴的直线上任意两点坐标的关系是(B)
A.纵坐标相等
B.横坐标相等
C.横坐标和纵坐标都相等
D.横坐标和纵坐标都不相等
15.点B的坐标为(3,-4),而直线AB平行于x轴,那么A点坐标有可能为(D)
A.(3,-2) B.(2,4)
C.(-3,2) D.(-3,-4)
16.过点A(1,-2)且垂直于y轴的直线,交y轴于点B,则点B的坐标为(C)
A.(0,1) B.(1,0)
C.(0,-2) D.(-2,0)
易错点1 对平面直角坐标系内点的坐标的符号理解不清
17.若点P(a,b)在第二象限,则点M(b-a,a-b)在(D)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
易错点2 点的位置不确定需要进行分类讨论
18.(2018·迁安市期末)已知点P(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是(3,3)或(6,-6).
02 中档题
19.在平面直角坐标系中,点M(-3,2)关于x轴对称的点在(C)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
20.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.若格点P(m-2,m+1)在第二象限,则m的值为(B)
A.0 B.0或1 C.2 D.2或3
21.在平面直角坐标系中,点P(m-3,4-2m)不可能在(A)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
22.(2018·石家庄高邑县期中)在平面直角坐标系中,已知线段AB∥x轴,端点A的坐标是(-1,4)且AB=4,则端点B的坐标是(D)
A.(-5,4) B.(3,4)
C.(-1,0) D.(-5,4)或(3,4)
23.若点A(m+2,3)与点B(-4,n+5)关于y轴对称,则m+n=0.
24.若A(a,b)在第二、四象限的夹角平分线上,则a与b的关系是a=-b.
25.如图所示.
(1)A,B两点关于y轴对称;
(2)A,D两点横坐标相等,线段AD平行于y轴,线段AD垂直于x轴;若点P是直线AD上任意一点,则点P的横坐标为-2;
(3)线段AB与CD的位置关系是平行,若点Q是直线AB上任意一点,则点Q的纵坐标为3.
26.(2017·沧州期中)如果|3x+3|+|x+3y-2|=0,那么点P(x,y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?
解:根据题意可得解得
所以点P(x,y),即P(-1,1)在第二象限,Q(x+1,y-1),即Q(0,0)在原点上.
03 综合题
27.图中显示10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时).
(1)用有序数对表示图中各点(先列后行);
(2)图中有一个点位于方格纸的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?
解:(1)(1,6),(1,9),(2,7),(3,5),(4,2),(5,5),(6,4),(7,2),(7,3),(9,1).
(2)用于看电视的时间和用于阅读课外书的时间相等.
(3)左上方的点表示用于阅读课外书的时间比用于看电视的时间多,右下方的点表示用于看电视的时间比用于阅读课外书的时间多.
(4)答案不唯一,略.
19.3 坐标与图形的位置
01 基础题
知识点1 在几何图形上建立平面直角坐标系
1.(2017·迁安期末)已知,长方形OABC按如图所示的方式放置在平面直角坐标系中,AB=4,BC=2,则点B的坐标为(C)
A.(4,2) B.(-2,4)
C.(4,-2) D.(-4,2)
2.方格纸上有M,N两点,如图所示,以N点为原点建立平面直角坐标系,则M点的坐标为(3,4).若以M点为原点建立平面直角坐标系,则N点的坐标为(A)
A.(-3,-4) B.(4,0)
C.(0,-2) D.(2,0)
3.如图是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,且C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为(D)
A.(2,3),(3,2) B.(3,2),(2,3)
C.(2,3),(-3,2) D.(3,2),(-2,3)
4.如图,线段AB上的任一点的坐标可以表示为(D)
A.(1,1) B.(1,y)(1≤y≤3)
C.(1,3) D.(x,1)(1≤x≤3)
知识点2 建立平面直角坐标系表示物体的位置
5.张强在某旅游景点的动物园的大门口看到该动物园的平面示意图,如图所示.若以大门为坐标原点,其他四个景点大致用坐标表示,肯定错误的是(C)
A.熊猫馆(1,4) B.猴山(6,1)
C.百鸟园(5,-3) D.驼峰(3,-2)
6.如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图.若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是(B)
A.景仁宫(4,2) B.养心殿(-2,3)
C.保和殿(1,0) D.武英殿(-3.5,-4)
7.如图为九嶷山风景区的几个景点的平面图,以舜帝陵为坐标原点,建立平面直角坐标系,则玉王宫岩所在位置的坐标为(2,4).
8.(教材P43习题A组T3变式)如图为某市部分简图,网格中每个小正方形的边长为1,请建立适当的平面直角坐标系,分别写出各地的坐标.
解:答案不唯一,可以以图中任何一个格点作为坐标原点.
如选火车站为原点建立平面直角坐标系.
则火车站(0,0),医院(-2,-2),文化宫(-3,1),体育场(-4,3),宾馆(2,2),市场(4,3),超市(2,-3).
02 中档题
9.如图,在方格纸上摆出了六枚棋子,如果用(2,-1)表示棋子A,用(6,-2)表示棋子B,那么(5,3)表示的是(A)
A.棋子E B.棋子D
C.棋子C D.棋子F
10.已知等边△ABC的边长为2,以BC的中点为原点,BC所在的直线为x轴,则点A的坐标为(B)
A.(,0)或(-,0) B.(0,)或(0,-)
C.(0,) D.(0,-)
11.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是(D)
A.(2,0) B.(4,0)
C.(-2,0) D.(3,0)
12.(2018·绵阳)如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,-1)和(-3,1),那么“卒”的坐标为(-2,-2).
13.在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(-3,1),(-2,-3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立平面直角坐标系并确定点C的位置;
(2)若同学们打算从点B处直接赶往C处,请用方位角和距离描述点C相对于点B的位置.
解:(1)如图所示.
(2)BC==5,所以点C在点B的北偏东45°方向上,距离点B 5 km处.
14.(2017·沧州期末)如图是某体育场看台台阶的一部分,如果A点的坐标为(0,0),B点的坐标为(1,1).
(1)请建立适当的平面直角坐标系,并写出点C,D,E,F的坐标;
(2)说明点B,C,D,E,F的坐标与点A的坐标相比较有什么变化?
(3)如果台阶有10级,你能求出该台阶的长度和高度吗?
解:(1)以A点为原点,水平方向为x轴,建立平面直角坐标系,如图所示.
则点C,D,E,F的坐标分别为C(2,2),D(3,3),E(4,4),F(5,5).
(2)点B,C,D,E,F的坐标与点A的坐标相比较,横坐标与纵坐标分别加1,2,3,4,5.
(3)每级台阶高为1,宽也为1,所以10级台阶的高度是10,长度为11.
03 综合题
15.(教材P43习题B组T1变式)如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
解:(1)当点B在点A的右边时,-1+3=2,
当点B在点A的左边时,-1-3=-4,
∴当点B的坐标为(2,0)或(-4,0).
(2)S△ABC=×3×4=6.
(3)设点P到x轴的距离为h,
则×3h=10,
解得h=.
当点P在y轴正半轴时,P(0,);
当点P在y轴负半轴时,P(0,-).
综上所述,点P的坐标为(0,)或(0,-).
周测(19.1~19.3)
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共40分)
1.(2018·大连)在平面直角坐标系中,点(-3,2)所在的象限是(B)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.下列数据不能确定物体位置的是(B)
A.5楼6号 B.北偏东30°
C.大学路19号 D.东经118°,北纬36°
3.如图,点A(-2,1)到x轴的距离为(B)
A.-2
B.1
C.2
D.
4.点M(1,2)关于y轴对称点的坐标为(A)
A.(-1,2) B.(-1,-2)
C.(1,-2) D.(2,-1)
5.点P(3,-5)和点Q(4,a)的连线垂直于y轴,则a的值为(D)
A.3 B.5 C.-3 D.-5
6.平面内点A(-1,2)和点B(-1,-2)的对称轴是(A)
A.x轴 B.y轴
C.直线y=4 D.直线x=-1
7.如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成(A)
A.(1,0) B.(-1,0)
C.(-1,1) D.(1,-1)
8.如图,四边形ABCD是长方形,AB=3,AD=4.已知A(-,-1),则点C的坐标是(D)
A.(-3,) B.(,-3)
C.(3,) D.(,3)
9.以下是甲、乙、丙三人看地图时对四个坐标的描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到邮局.
丙:邮局在火车站西200米处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站(A)
A.向南直走300米,再向西直走200米
B.向南直走300米,再向西直走100米
C.向南直走700米,再向西直走200米
D.向南直走700米,再向西直走600米
10.已知点A(-1,0),B(2,0),在y轴上存在一点C,使△ABC的面积为6,则点C的坐标为(D)
A.(0,4) B.(0,2)
C.(0,2)或(0,-2) D.(0,4)或(0,-4)
二、填空题(每小题4分,共20分)
11.剧院里5排2号可以用(5,2)表示,则(7,4)表示7排4号.
12.(2018·唐山滦县期末)若点P(1-m,2+m)在第一象限,则m的取值范围是-213.(2018·大庆)在平面直角坐标系中,点A的坐标为(a,3),点B的坐标为(4,b).若点A与点B关于原点O对称,则ab=12.
14.若干个英语字母打乱顺序后排成了如图所示的方阵.若字母L表示为(1,4),则按(3,4),(2,2),(1,3),(4,1)的顺序排列成的英语单词为PARE.
15.“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表示式为S=a+-1,小明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数.请你根据图1推断公式中表示多边形内部整点个数的字母是a,并运用这个公式求得图2中多边形的面积是17.5.
三、解答题(共40分)
16.(8分)图中标明了小英家附近的一些地方.以小英家为坐标原点,建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(0,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
解:(1)汽车站(1,1),消防站(2,-2);
(2)小英路上经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
17.(10分)如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
解:(1)A(-2,1),B(-3,-2),C(3,-2),D(1,2).
(2)S四边形ABCD=3×3+2××1×3+×2×4=16.
18.(10分)已知点P(2m+4,m-1).试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过点A(2,-3),且与x轴平行的直线上.
解:(1)令2m+4=0,解得m=-2,
所以点P的坐标为(0,-3).
(2)令m-1=0,解得m=1,所以点P的坐标为(6,0).
(3)令m-1=(2m+4)+3,解得m=-8,
所以点P的坐标为(-12,-9).
(4)令m-1=-3,解得m=-2.
所以点P的坐标为(0,-3).
19.(12分)(2017·河北模拟)如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=4,b=6,点B的坐标为(4,6);
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
解:(2)∵点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动,
∴2×4=8.
∵OA=4,OC=6,
∴当点P移动4秒时,在线段CB上,离点C的距离是8-6=2个单位长度,点P的坐标是(2,6).
(3)由题意可得,在移动过程中,当点P到x轴的距离为5个单位长度时,存在两种情况:
第一种情况,当点P在OC上时,
点P移动的时间是5÷2=2.5(秒);
第二种情况,当点P在BA上时,
点P移动的时间是(6+4+1)÷2=5.5(秒),
故在移动过程中,当点P到x轴的距离为5个单位长度时,点P移动的时间是2.5秒或5.5秒.
19.4 坐标与图形的变化
第1课时 坐标与图形的平移
01 基础题
知识点 坐标与图形的平移
1.在平面直角坐标系中,将点A(-2,1)向左平移2个单位长度到点Q,则点Q的坐标为(C)
A.(-2,3) B.(0,1)
C.(-4,1) D.(-4,-1)
2.(2018·唐山丰南区期中)在平面直角坐标系中,将三角形各点的纵坐标都减去1,横坐标保持不变,所得图形与原图形相比(D)
A.向右平移了1个单位长度
B.向左平移了1个单位长度
C.向上平移了1个单位长度
D.向下平移了1个单位长度
3.(2018·抚顺)已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(-2,1),则点B的对应点的坐标为(C)
A.(5,3) B.(-1,-2)
C.(-1,-1) D.(0,-1)
4.在平面直角坐标系中,将点P(3,2)沿x轴的负方向平移4个单位长度,再沿y轴正方向平移4个单位长度,所得到点的坐标是(D)
A.(-1,2) B.(3,-2)
C.(-2,-1) D.(-1,6)
5.如图,在6×10的网格中,△DEF是△ABC平移后的图形,那么△ABC经过何种变换可得到△DEF(B)
A.向左平移4个单位长度,再向下平移1个单位长度
B.向右平移4个单位长度,再向上平移1个单位长度
C.向左平移1个单位长度,再向下平移4个单位长度
D.向右平移4个单位长度,再向下平移1个单位长度
6.如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是(A)
A.(-2,-4) B.(-2,4)
C.(2,-3) D.(-1,-3)
7.在同一平面直角坐标系中,图形M向上平移3个单位长度得到图形N,如果图形M上某点A的坐标为(5,-6),那么图形N上与点A对应的点A′的坐标是(B)
A.(5,-9) B.(5,-3)
C.(2,-6) D.(8,-6)
8.在平面直角坐标系中,一只青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2个单位长度到点A′处,则点A′的坐标为(1,2).
9.在平面直角坐标系中,已知点A(-4,0),B(0,2),现将线段AB向右平移,使点A与坐标原点O重合,则点B平移后的坐标是(4,2).
10.在如图所示的平面直角坐标系中,将三角形向左平移3个单位长度,再向下平移4个单位长度.
(1)画出平移后的图形,并写出平移后三个顶点的坐标;
(2)若三角形上一点坐标为(a,b),写出平移后对应点的坐标.
解:(1)所作图形如图.
平移后三个顶点的坐标分别为(-1,3),(1,0),(-4,-3).
(2)点(a,b)平移后的坐标为(a-3,b-4).
易错点1 平移的方向不确定而致错
11.△ABC的顶点A坐标为(-2,5),若将△ABC沿x轴平移5个单位长度,则A点坐标变为(C)
A.(3,5) B.(3,0)或(-7,0)
C.(3,5)或(-7,5) D.(-2,0)或(-2,10)
易错点2 混淆点的平移与坐标系的平移
12.已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是(-5,1).
02 中档题
13.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是(D)
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
14.(2018·沙河期末)如图,线段AB两端点的坐标分别为A(-1,0),B(1,1),把线段AB平移到CD位置.若线段CD两端点的坐标分别为C(1,a),D(b,4),则a+b的值为(B)
A.7 B.6 C.5 D.4
15.已知点M(3a-9,1-a),将点M向右平移3个单位长度后落在y轴上,则点M的坐标为(-3,-1).
16.(教材P46习题A组T2变式)△ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1)分别写出点A′,B′,C′的坐标;
(2)说明△A′B′C′由△ABC经过怎样的平移得到?
(3)若点P(a,b)是△ABC内部一点,写出平移后△A′B′C′内的对应点P′的坐标;
(4)求△ABC的面积.
解:(1)A′(-3,1),B′(-2,-2),C′(-1,-1).
(2)△ABC先向左平移4个单位长度,再向下平移2个单位长度得到△A′B′C′.
(3)P′(a-4,b-2).
(4)S△ABC=6-×2×2-×1×3-×1×1=2.
17.如图所示的平面直角坐标系中,四边形ABCD的四个顶点的坐标分别是A(1,2),B(3,-2),C(5,1),D(4,4).
(1)求四边形ABCD的面积;
(2)把四边形ABCD向左平移3个单位长度得到四边形A1B1C1D1,画出平移后的四边形,并写出平移后四边形各个顶点的坐标.
解:(1)S四边形ABCD=4×6-×2×3-×2×4-×2×3-×1×3=12.5.
(2)如图所示.
由图可知:A1(-2,2),B1(0,-2),C1(2,1),D1(1,4).
03 综合题
18.在平面直角坐标系中,一只蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断爬行,每次爬行1个单位长度,其爬行路线如下图所示.
(1)填写下列各点的坐标:A4(2,0),A8(4,0),A12(6,0);
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的爬行方向.
解:(2)A4n(2n,0).
(3)向上.
第2课时 坐标与图形的轴对称、放缩
01 基础题
知识点1 坐标与图形的轴对称
1.如图,△ABC与△DEF关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为(B)
A.(-4,6) B.(4,6)
C.(-2,1) D.(6,2)
2.已知△ABC是平面直角坐标系中任意位置的一个三角形,现将△ABC各顶点的纵坐标乘-1,得到△A1B1C1,则它与△ABC的位置关系是(A)
A.关于x轴对称
B.关于y轴对称
C.关于直线x=-1对称
D.关于直线y=-1对称
3.如图,△ABC中顶点B在坐标原点,顶点A坐标为(2,2),将△ABC沿x轴翻折到第四象限,则点A的对称点A′的坐标为(2,-2).
4.在平面直角坐标系中,已知A(2,3),B(1,-2),C(2,-3),D(1,2),则AB与CD关于x轴对称.
5.在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC及与△ABC关于y轴对称的图形.
解:如图所示,△DEF与△ABC关于y轴对称.
6.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1),B(3,-3),C(0,-4).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)画出△A1B1C1关于y轴对称的
△A2B2C2.
解:(1)△A1B1C1如图所示.
(2)△A2B2C2如图所示.
知识点2 坐标与图形的放缩
7.如图所示的鱼,各点纵坐标不变,横坐标乘2,所得图形与原图形相比(A)
A.形状大小变了,鱼整体被横向拉长为原来的2倍
B.形状大小变了,鱼整体被纵向拉长为原来的2倍
C.形状大小不变,鱼整体向右移动了两个单位长度
D.形状大小不变,鱼整体向左移动了两个单位长度
8.将△ABC各顶点的纵坐标乘2,得新△A′B′C′.若△ABC各顶点的坐标分别为A(-2,0),B(2,0),C(0,2),则下列图像中正确的是(C)
9.已知平面直角坐标系中长方形ABCD.
(1)将长方形上各个点的横坐标不变,纵坐标分别乘,则所得图形与原图形相比被纵向压缩为原来的;
(2)将长方形上各个点的纵坐标不变,横坐标分别减去2,则所得图形与原图形相比向左平移了2个单位长度;
(3)若A(2,1),B(4,1),将长方形横向伸长为原来的2倍,则A,B两点变化后的坐标分别为(4,1),(8,1),变化后的长方形的面积是原来的长方形面积的2倍.
02 中档题
10.把△ABC各点的横坐标都乘-1,纵坐标不变,符合上述要求的图是(B)
11.如图,△ABC在平面直角坐标系的第二象限内,顶点A的坐标是(-2,3),先把△ABC向下平移4个单位长度得到△A1B1C1,再作△A1B1C1关于y轴对称的图形△A2B2C2,则顶点A2的坐标是(B)
A.(-3,2) B.(2,-1) C.(1,-2) D.(3,-1)
12.(2018·邢台四校期中联考)平面直角坐标系中的四边形ABCD,各顶点的横、纵坐标均扩大为原来的2倍,四边形ABCD的形状不变(填“改变”或“不变”),面积变为原来的4倍.
13.如图,在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
①(4,5),(0,3),(1,3),(7,3),(8,3),(4,5);
②(1,3),(1,0),(7,0),(7,3).
(1)观察所得的图形,你觉得它像什么?
(2)求出这个图形的面积;
(3)怎样变换坐标,才能使得到的图形与(1)中的图形关于x轴对称.
解:如图所示.
(1)像一所“房子”.
(2)此图形的面积为×8×2+6×3=26.
(3)将各点的纵坐标乘-1,横坐标保持不变,所得的图形与(1)中的图形关于x轴对称.
14.在平面直角坐标系中画出一个以A(-1,-1),B(2,-1),C(2,2),D(-1,2)为顶点的图形,说明这是什么图形?把各顶点的坐标都乘2,得到的图形的面积与原图形面积有怎样的关系?你再做一做用不同的k(k>0)值去乘各顶点的坐标,发现随着k的变化,图形的面积是怎样变化的?
解:如图,画出以A,B,C,D为顶点的图形,这是一个正方形,它的边长为3.
把各顶点的坐标都乘2,得A′(-2,-2),B′(4,-2),C′(4,4),D′(-2,4),画出一个正方形,它的边长是6,所画正方形的面积是原正方形面积的4倍.
若把各顶点的坐标乘k(k>1),则所得图形面积为原图形面积的k2倍;若把各顶点的坐标乘k(0<k<1),则所得图形面积缩小为原图形面积的k2.
03 综合题
15.(2017·沧州期中)如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标是(16,3),B4的坐标是(32,0);
(2)若按(1)中的变换,将△OAB进行n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,推测An的坐标是(2n,3),Bn的坐标是(2n+1,0).
19.1 确定平面上物体的位置
01 基础题
知识点1 用有序实数对表示物体的位置
1.如图,一方队正沿箭头所指的方向前进, A的位置为三列四行,表示为(3,4),那么B 的位置是(A)
A.(4,5) B.(5,4) C.(4,2) D.(4,3)
2.若将7门6楼简记为(7,6),则6门7楼可简记为(6,7),(8,5)表示的意义是8门5楼.
知识点2 用“方位角+距离”表示物体的位置
3.已知古塔在嘉淇的北偏东30°方向,且距离嘉淇2 km,符合条件的示意图是(B)
易错点 忽视点的位置需要用一对数来表示
4.(2018·邢台宁晋县期末)以下描述中,能确定具体位置的是(D)
A.万达电影院2排
B.距薛城高铁站2千米
C.北偏东30 ℃
D.东经106 ℃,北纬31 ℃
02 中档题
5.在一座共8层的商业大厦中,每层的摊位布局基本相同.小明的父亲在6楼的位置如图所示,其位置可以表示为(6,2,3).若小明的母亲在5楼,其摊位也可以用如图表示,则小明母亲的摊位的位置可以表示为(5,4,2).
6.(2017·石家庄长安区期中)如图,线段OB,OC,OA的长度分别是1,2,3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),则C点可表示为(2,75°).
7.(教材P31“观察与思考”变式)如图是某次海战中敌我双方战舰对峙示意图(图中1 cm表示20海里).
(1)在我方潜艇的北偏东40°有哪些目标?要想确定敌方战舰B的位置,还需要什么数据?
(2)距离我方潜艇20海里的敌方战舰有哪几艘?
(3)敌方战舰C和敌方战舰A分别在我方潜艇的什么方向?
(4)要确定每艘敌方战舰的位置,都需要哪些数据?
解:(1)在我方潜艇的北偏东40°有敌方战舰B和小岛;要想确定敌方战舰B的位置,还需要知道敌方战舰B与我方潜艇的距离.
(2)距离我方潜艇20海里的敌方战舰有敌方战舰A和C.
(3)敌方战舰C在我方潜艇的正东方向,敌方战舰A在我方潜艇的正南方向.
(4)要确定每艘敌方战舰的位置,需要知道每艘敌方战舰分别在什么方向,与我方潜艇的距离是多少.
8.(2018·唐山滦南县二模)如图,点A在观测点北偏东30°方向,且与观测点的距离为8 km,将点A的位置记作A(8,30°).用同样的方法将点B、点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在(A)
A.点O1 B.点O2 C.点O3 D.点O4
19.2 平面直角坐标系
第1课时 平面直角坐标系中点的坐标表示
01 基础题
知识点1 用坐标表示点
1.如图,在平面直角坐标系中,点P的坐标为(A)
A.(3,-2)
B.(-2,3)
C.(-3,2)
D.(2,-3)
2.(教材P37习题A组T2变式)如图是某公园的几个景点的分布示意图(图中每个小正方形边长为1个单位长度).请建立以猴山为坐标原点,以水平向右为x轴正方向,以竖直向上为y轴正方向的平面直角坐标系,用坐标表示下列景点的位置:
解:儿童乐园 (2,-2);花窖 (-2,-3);瞪眼岭 (-1,3);仙人掌 (3,3).
知识点2 已知坐标描点
3.某市有A,B,C,D四个大型超市,分别位于一条东西走向的平安大路两侧,如图所示,根据如图建立的平面直角坐标系,已知四个超市的坐标分别为(10,4),(-2,2.5),(6,-4),(0,-3).写出四个坐标相应的超市是A,C,B,D.
4.如图,在所给平面直角坐标系中作出点A(2,-3),B(-1,2),C(0,-2),D(-3,-1),并写出点P,Q,M的坐标分别为P(2.5,0),Q(-1,3),M(0,-3).
02 中档题
5.(2017·唐山滦南县期中)平面直角坐标系中x轴的上方有一点P,它到x轴的距离为2,到y轴的距离为3,则点P的坐标为(C)
A.(3,2) B.(-3,2)
C.(3,2)或(-3,2) D.(2,3)
6.(教材P38习题B组T1变式)一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是(A)
A.(30-50,30) B.(30,30-50)
C.(30,30) D.(30,30)
7.若点P(x,y)的坐标满足x+y=xy,则称点P为“和谐点”.请写出一个“和谐点”的坐标:(2,2)或(0,0)(答案不唯一).
8.如图是某公园的平面图(每个方格的边长为100 m).
(1)写出任意五个景点的坐标;
(2)某星期天的上午,苗苗在公园沿(-500,0),(-200,-100),(200,-200),(300,200),(500,0)的路线游玩了半天,请你写出她路上经过的地方.
解:(1)答案不唯一,如:湖心亭(-300,200),望春亭(-200,-100),音乐台(0,400),牡丹园(300,200),游乐园(200,-200).
(2)西门→望春亭→游乐园→牡丹园→东门.
03 综合题
9. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(0,0)→(1,0)→(1,1)→(2,2)→(2,1)→(2,0)…根据这个规律探索可得,第100个点的坐标是(13,8).
第2课时 平面直角坐标系中点的坐标特征
01 基础题
知识点1 坐标平面内点的坐标特征
1.(2017·石家庄长安区期中)在平面直角坐标系中,点(1,5)所在的象限是(A)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.(2018·邢台隆尧县期末)下列各点在第四象限的是(C)
A.(1,2) B.(-1,2)
C.(1,-2) D.(-1,-2)
3.下列各点中,在坐标轴上的是(B)
A.(3,3) B.(-3,0)
C.(-1,2) D.(-2,-3)
4.(2018·扬州)在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是(C)
A.(3,-4) B.(4,-3)
C.(-4,3) D.(-3,4)
5.如图,小手盖住的点的坐标可能为(D)
A.(5,2)
B.(-6,3)
C.(-4,-6)
D.(3,-4)
6.若xy=0,则点P(x,y)一定在(C)
A.x轴上 B.y轴上
C.坐标轴上 D.原点
7.(2018·唐山路北区期末)点P(m+3,m+1)在平面直角坐标系的x轴上,则点P的坐标为(B)
A.(0,-2) B.(2,0)
C.(4,0) D.(0,-4)
8.若点A(x,2)在第二象限,则x的取值范围是x<0.
9.写出一个平面直角坐标系中第三象限内点的坐标:(-2,-1)(答案不唯一).
知识点2 关于x轴(或y轴,或原点)对称的两个点的坐标
10.(2018·武汉)点A(2,-5)关于x轴对称的点的坐标是(A)
A.(2,5) B.(-2,5)
C.(-2,-5) D.(-5,2)
11.(2018·湘潭)如图,点A的坐标为(-1,2),则点A关于y轴的对称点的坐标为(A)
A.(1,2)
B.(-1,-2)
C.(1,-2)
D.(2,-1)
12.(2017·湖州)在平面直角坐标系中,点P(1,2)关于原点的对称点P′的坐标是(D)
A.(1,2) B.(-1,2)
C.(1,-2) D.(-1,-2)
13.小明将某点关于x轴的对称点误认为是关于y轴的对称点,得到点(-2,-3),求该点坐标及其关于x轴、原点的对称点的坐标.
解:因为小明将所求点误认为是关于y轴的对称点而得到点(-2,-3),因此可得该点坐标是(2,-3).所以该点关于x轴的对称点的坐标为(2,3),关于原点的对称点的坐标为(-2,3).
知识点3 平行(或垂直)于坐标轴的直线上点的坐标
14.(教材P40习题B组T2变式)平行于y轴的直线上任意两点坐标的关系是(B)
A.纵坐标相等
B.横坐标相等
C.横坐标和纵坐标都相等
D.横坐标和纵坐标都不相等
15.点B的坐标为(3,-4),而直线AB平行于x轴,那么A点坐标有可能为(D)
A.(3,-2) B.(2,4)
C.(-3,2) D.(-3,-4)
16.过点A(1,-2)且垂直于y轴的直线,交y轴于点B,则点B的坐标为(C)
A.(0,1) B.(1,0)
C.(0,-2) D.(-2,0)
易错点1 对平面直角坐标系内点的坐标的符号理解不清
17.若点P(a,b)在第二象限,则点M(b-a,a-b)在(D)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
易错点2 点的位置不确定需要进行分类讨论
18.(2018·迁安市期末)已知点P(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是(3,3)或(6,-6).
02 中档题
19.在平面直角坐标系中,点M(-3,2)关于x轴对称的点在(C)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
20.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.若格点P(m-2,m+1)在第二象限,则m的值为(B)
A.0 B.0或1 C.2 D.2或3
21.在平面直角坐标系中,点P(m-3,4-2m)不可能在(A)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
22.(2018·石家庄高邑县期中)在平面直角坐标系中,已知线段AB∥x轴,端点A的坐标是(-1,4)且AB=4,则端点B的坐标是(D)
A.(-5,4) B.(3,4)
C.(-1,0) D.(-5,4)或(3,4)
23.若点A(m+2,3)与点B(-4,n+5)关于y轴对称,则m+n=0.
24.若A(a,b)在第二、四象限的夹角平分线上,则a与b的关系是a=-b.
25.如图所示.
(1)A,B两点关于y轴对称;
(2)A,D两点横坐标相等,线段AD平行于y轴,线段AD垂直于x轴;若点P是直线AD上任意一点,则点P的横坐标为-2;
(3)线段AB与CD的位置关系是平行,若点Q是直线AB上任意一点,则点Q的纵坐标为3.
26.(2017·沧州期中)如果|3x+3|+|x+3y-2|=0,那么点P(x,y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?
解:根据题意可得解得
所以点P(x,y),即P(-1,1)在第二象限,Q(x+1,y-1),即Q(0,0)在原点上.
03 综合题
27.图中显示10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时).
(1)用有序数对表示图中各点(先列后行);
(2)图中有一个点位于方格纸的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?
解:(1)(1,6),(1,9),(2,7),(3,5),(4,2),(5,5),(6,4),(7,2),(7,3),(9,1).
(2)用于看电视的时间和用于阅读课外书的时间相等.
(3)左上方的点表示用于阅读课外书的时间比用于看电视的时间多,右下方的点表示用于看电视的时间比用于阅读课外书的时间多.
(4)答案不唯一,略.
19.3 坐标与图形的位置
01 基础题
知识点1 在几何图形上建立平面直角坐标系
1.(2017·迁安期末)已知,长方形OABC按如图所示的方式放置在平面直角坐标系中,AB=4,BC=2,则点B的坐标为(C)
A.(4,2) B.(-2,4)
C.(4,-2) D.(-4,2)
2.方格纸上有M,N两点,如图所示,以N点为原点建立平面直角坐标系,则M点的坐标为(3,4).若以M点为原点建立平面直角坐标系,则N点的坐标为(A)
A.(-3,-4) B.(4,0)
C.(0,-2) D.(2,0)
3.如图是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,且C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为(D)
A.(2,3),(3,2) B.(3,2),(2,3)
C.(2,3),(-3,2) D.(3,2),(-2,3)
4.如图,线段AB上的任一点的坐标可以表示为(D)
A.(1,1) B.(1,y)(1≤y≤3)
C.(1,3) D.(x,1)(1≤x≤3)
知识点2 建立平面直角坐标系表示物体的位置
5.张强在某旅游景点的动物园的大门口看到该动物园的平面示意图,如图所示.若以大门为坐标原点,其他四个景点大致用坐标表示,肯定错误的是(C)
A.熊猫馆(1,4) B.猴山(6,1)
C.百鸟园(5,-3) D.驼峰(3,-2)
6.如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图.若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是(B)
A.景仁宫(4,2) B.养心殿(-2,3)
C.保和殿(1,0) D.武英殿(-3.5,-4)
7.如图为九嶷山风景区的几个景点的平面图,以舜帝陵为坐标原点,建立平面直角坐标系,则玉王宫岩所在位置的坐标为(2,4).
8.(教材P43习题A组T3变式)如图为某市部分简图,网格中每个小正方形的边长为1,请建立适当的平面直角坐标系,分别写出各地的坐标.
解:答案不唯一,可以以图中任何一个格点作为坐标原点.
如选火车站为原点建立平面直角坐标系.
则火车站(0,0),医院(-2,-2),文化宫(-3,1),体育场(-4,3),宾馆(2,2),市场(4,3),超市(2,-3).
02 中档题
9.如图,在方格纸上摆出了六枚棋子,如果用(2,-1)表示棋子A,用(6,-2)表示棋子B,那么(5,3)表示的是(A)
A.棋子E B.棋子D
C.棋子C D.棋子F
10.已知等边△ABC的边长为2,以BC的中点为原点,BC所在的直线为x轴,则点A的坐标为(B)
A.(,0)或(-,0) B.(0,)或(0,-)
C.(0,) D.(0,-)
11.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是(D)
A.(2,0) B.(4,0)
C.(-2,0) D.(3,0)
12.(2018·绵阳)如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,-1)和(-3,1),那么“卒”的坐标为(-2,-2).
13.在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(-3,1),(-2,-3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立平面直角坐标系并确定点C的位置;
(2)若同学们打算从点B处直接赶往C处,请用方位角和距离描述点C相对于点B的位置.
解:(1)如图所示.
(2)BC==5,所以点C在点B的北偏东45°方向上,距离点B 5 km处.
14.(2017·沧州期末)如图是某体育场看台台阶的一部分,如果A点的坐标为(0,0),B点的坐标为(1,1).
(1)请建立适当的平面直角坐标系,并写出点C,D,E,F的坐标;
(2)说明点B,C,D,E,F的坐标与点A的坐标相比较有什么变化?
(3)如果台阶有10级,你能求出该台阶的长度和高度吗?
解:(1)以A点为原点,水平方向为x轴,建立平面直角坐标系,如图所示.
则点C,D,E,F的坐标分别为C(2,2),D(3,3),E(4,4),F(5,5).
(2)点B,C,D,E,F的坐标与点A的坐标相比较,横坐标与纵坐标分别加1,2,3,4,5.
(3)每级台阶高为1,宽也为1,所以10级台阶的高度是10,长度为11.
03 综合题
15.(教材P43习题B组T1变式)如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
解:(1)当点B在点A的右边时,-1+3=2,
当点B在点A的左边时,-1-3=-4,
∴当点B的坐标为(2,0)或(-4,0).
(2)S△ABC=×3×4=6.
(3)设点P到x轴的距离为h,
则×3h=10,
解得h=.
当点P在y轴正半轴时,P(0,);
当点P在y轴负半轴时,P(0,-).
综上所述,点P的坐标为(0,)或(0,-).
周测(19.1~19.3)
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共40分)
1.(2018·大连)在平面直角坐标系中,点(-3,2)所在的象限是(B)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.下列数据不能确定物体位置的是(B)
A.5楼6号 B.北偏东30°
C.大学路19号 D.东经118°,北纬36°
3.如图,点A(-2,1)到x轴的距离为(B)
A.-2
B.1
C.2
D.
4.点M(1,2)关于y轴对称点的坐标为(A)
A.(-1,2) B.(-1,-2)
C.(1,-2) D.(2,-1)
5.点P(3,-5)和点Q(4,a)的连线垂直于y轴,则a的值为(D)
A.3 B.5 C.-3 D.-5
6.平面内点A(-1,2)和点B(-1,-2)的对称轴是(A)
A.x轴 B.y轴
C.直线y=4 D.直线x=-1
7.如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成(A)
A.(1,0) B.(-1,0)
C.(-1,1) D.(1,-1)
8.如图,四边形ABCD是长方形,AB=3,AD=4.已知A(-,-1),则点C的坐标是(D)
A.(-3,) B.(,-3)
C.(3,) D.(,3)
9.以下是甲、乙、丙三人看地图时对四个坐标的描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到邮局.
丙:邮局在火车站西200米处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站(A)
A.向南直走300米,再向西直走200米
B.向南直走300米,再向西直走100米
C.向南直走700米,再向西直走200米
D.向南直走700米,再向西直走600米
10.已知点A(-1,0),B(2,0),在y轴上存在一点C,使△ABC的面积为6,则点C的坐标为(D)
A.(0,4) B.(0,2)
C.(0,2)或(0,-2) D.(0,4)或(0,-4)
二、填空题(每小题4分,共20分)
11.剧院里5排2号可以用(5,2)表示,则(7,4)表示7排4号.
12.(2018·唐山滦县期末)若点P(1-m,2+m)在第一象限,则m的取值范围是-2
14.若干个英语字母打乱顺序后排成了如图所示的方阵.若字母L表示为(1,4),则按(3,4),(2,2),(1,3),(4,1)的顺序排列成的英语单词为PARE.
15.“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表示式为S=a+-1,小明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数.请你根据图1推断公式中表示多边形内部整点个数的字母是a,并运用这个公式求得图2中多边形的面积是17.5.
三、解答题(共40分)
16.(8分)图中标明了小英家附近的一些地方.以小英家为坐标原点,建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(0,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
解:(1)汽车站(1,1),消防站(2,-2);
(2)小英路上经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
17.(10分)如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
解:(1)A(-2,1),B(-3,-2),C(3,-2),D(1,2).
(2)S四边形ABCD=3×3+2××1×3+×2×4=16.
18.(10分)已知点P(2m+4,m-1).试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过点A(2,-3),且与x轴平行的直线上.
解:(1)令2m+4=0,解得m=-2,
所以点P的坐标为(0,-3).
(2)令m-1=0,解得m=1,所以点P的坐标为(6,0).
(3)令m-1=(2m+4)+3,解得m=-8,
所以点P的坐标为(-12,-9).
(4)令m-1=-3,解得m=-2.
所以点P的坐标为(0,-3).
19.(12分)(2017·河北模拟)如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=4,b=6,点B的坐标为(4,6);
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
解:(2)∵点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动,
∴2×4=8.
∵OA=4,OC=6,
∴当点P移动4秒时,在线段CB上,离点C的距离是8-6=2个单位长度,点P的坐标是(2,6).
(3)由题意可得,在移动过程中,当点P到x轴的距离为5个单位长度时,存在两种情况:
第一种情况,当点P在OC上时,
点P移动的时间是5÷2=2.5(秒);
第二种情况,当点P在BA上时,
点P移动的时间是(6+4+1)÷2=5.5(秒),
故在移动过程中,当点P到x轴的距离为5个单位长度时,点P移动的时间是2.5秒或5.5秒.
19.4 坐标与图形的变化
第1课时 坐标与图形的平移
01 基础题
知识点 坐标与图形的平移
1.在平面直角坐标系中,将点A(-2,1)向左平移2个单位长度到点Q,则点Q的坐标为(C)
A.(-2,3) B.(0,1)
C.(-4,1) D.(-4,-1)
2.(2018·唐山丰南区期中)在平面直角坐标系中,将三角形各点的纵坐标都减去1,横坐标保持不变,所得图形与原图形相比(D)
A.向右平移了1个单位长度
B.向左平移了1个单位长度
C.向上平移了1个单位长度
D.向下平移了1个单位长度
3.(2018·抚顺)已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(-2,1),则点B的对应点的坐标为(C)
A.(5,3) B.(-1,-2)
C.(-1,-1) D.(0,-1)
4.在平面直角坐标系中,将点P(3,2)沿x轴的负方向平移4个单位长度,再沿y轴正方向平移4个单位长度,所得到点的坐标是(D)
A.(-1,2) B.(3,-2)
C.(-2,-1) D.(-1,6)
5.如图,在6×10的网格中,△DEF是△ABC平移后的图形,那么△ABC经过何种变换可得到△DEF(B)
A.向左平移4个单位长度,再向下平移1个单位长度
B.向右平移4个单位长度,再向上平移1个单位长度
C.向左平移1个单位长度,再向下平移4个单位长度
D.向右平移4个单位长度,再向下平移1个单位长度
6.如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是(A)
A.(-2,-4) B.(-2,4)
C.(2,-3) D.(-1,-3)
7.在同一平面直角坐标系中,图形M向上平移3个单位长度得到图形N,如果图形M上某点A的坐标为(5,-6),那么图形N上与点A对应的点A′的坐标是(B)
A.(5,-9) B.(5,-3)
C.(2,-6) D.(8,-6)
8.在平面直角坐标系中,一只青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2个单位长度到点A′处,则点A′的坐标为(1,2).
9.在平面直角坐标系中,已知点A(-4,0),B(0,2),现将线段AB向右平移,使点A与坐标原点O重合,则点B平移后的坐标是(4,2).
10.在如图所示的平面直角坐标系中,将三角形向左平移3个单位长度,再向下平移4个单位长度.
(1)画出平移后的图形,并写出平移后三个顶点的坐标;
(2)若三角形上一点坐标为(a,b),写出平移后对应点的坐标.
解:(1)所作图形如图.
平移后三个顶点的坐标分别为(-1,3),(1,0),(-4,-3).
(2)点(a,b)平移后的坐标为(a-3,b-4).
易错点1 平移的方向不确定而致错
11.△ABC的顶点A坐标为(-2,5),若将△ABC沿x轴平移5个单位长度,则A点坐标变为(C)
A.(3,5) B.(3,0)或(-7,0)
C.(3,5)或(-7,5) D.(-2,0)或(-2,10)
易错点2 混淆点的平移与坐标系的平移
12.已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是(-5,1).
02 中档题
13.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是(D)
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
14.(2018·沙河期末)如图,线段AB两端点的坐标分别为A(-1,0),B(1,1),把线段AB平移到CD位置.若线段CD两端点的坐标分别为C(1,a),D(b,4),则a+b的值为(B)
A.7 B.6 C.5 D.4
15.已知点M(3a-9,1-a),将点M向右平移3个单位长度后落在y轴上,则点M的坐标为(-3,-1).
16.(教材P46习题A组T2变式)△ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1)分别写出点A′,B′,C′的坐标;
(2)说明△A′B′C′由△ABC经过怎样的平移得到?
(3)若点P(a,b)是△ABC内部一点,写出平移后△A′B′C′内的对应点P′的坐标;
(4)求△ABC的面积.
解:(1)A′(-3,1),B′(-2,-2),C′(-1,-1).
(2)△ABC先向左平移4个单位长度,再向下平移2个单位长度得到△A′B′C′.
(3)P′(a-4,b-2).
(4)S△ABC=6-×2×2-×1×3-×1×1=2.
17.如图所示的平面直角坐标系中,四边形ABCD的四个顶点的坐标分别是A(1,2),B(3,-2),C(5,1),D(4,4).
(1)求四边形ABCD的面积;
(2)把四边形ABCD向左平移3个单位长度得到四边形A1B1C1D1,画出平移后的四边形,并写出平移后四边形各个顶点的坐标.
解:(1)S四边形ABCD=4×6-×2×3-×2×4-×2×3-×1×3=12.5.
(2)如图所示.
由图可知:A1(-2,2),B1(0,-2),C1(2,1),D1(1,4).
03 综合题
18.在平面直角坐标系中,一只蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断爬行,每次爬行1个单位长度,其爬行路线如下图所示.
(1)填写下列各点的坐标:A4(2,0),A8(4,0),A12(6,0);
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的爬行方向.
解:(2)A4n(2n,0).
(3)向上.
第2课时 坐标与图形的轴对称、放缩
01 基础题
知识点1 坐标与图形的轴对称
1.如图,△ABC与△DEF关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为(B)
A.(-4,6) B.(4,6)
C.(-2,1) D.(6,2)
2.已知△ABC是平面直角坐标系中任意位置的一个三角形,现将△ABC各顶点的纵坐标乘-1,得到△A1B1C1,则它与△ABC的位置关系是(A)
A.关于x轴对称
B.关于y轴对称
C.关于直线x=-1对称
D.关于直线y=-1对称
3.如图,△ABC中顶点B在坐标原点,顶点A坐标为(2,2),将△ABC沿x轴翻折到第四象限,则点A的对称点A′的坐标为(2,-2).
4.在平面直角坐标系中,已知A(2,3),B(1,-2),C(2,-3),D(1,2),则AB与CD关于x轴对称.
5.在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC及与△ABC关于y轴对称的图形.
解:如图所示,△DEF与△ABC关于y轴对称.
6.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1),B(3,-3),C(0,-4).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)画出△A1B1C1关于y轴对称的
△A2B2C2.
解:(1)△A1B1C1如图所示.
(2)△A2B2C2如图所示.
知识点2 坐标与图形的放缩
7.如图所示的鱼,各点纵坐标不变,横坐标乘2,所得图形与原图形相比(A)
A.形状大小变了,鱼整体被横向拉长为原来的2倍
B.形状大小变了,鱼整体被纵向拉长为原来的2倍
C.形状大小不变,鱼整体向右移动了两个单位长度
D.形状大小不变,鱼整体向左移动了两个单位长度
8.将△ABC各顶点的纵坐标乘2,得新△A′B′C′.若△ABC各顶点的坐标分别为A(-2,0),B(2,0),C(0,2),则下列图像中正确的是(C)
9.已知平面直角坐标系中长方形ABCD.
(1)将长方形上各个点的横坐标不变,纵坐标分别乘,则所得图形与原图形相比被纵向压缩为原来的;
(2)将长方形上各个点的纵坐标不变,横坐标分别减去2,则所得图形与原图形相比向左平移了2个单位长度;
(3)若A(2,1),B(4,1),将长方形横向伸长为原来的2倍,则A,B两点变化后的坐标分别为(4,1),(8,1),变化后的长方形的面积是原来的长方形面积的2倍.
02 中档题
10.把△ABC各点的横坐标都乘-1,纵坐标不变,符合上述要求的图是(B)
11.如图,△ABC在平面直角坐标系的第二象限内,顶点A的坐标是(-2,3),先把△ABC向下平移4个单位长度得到△A1B1C1,再作△A1B1C1关于y轴对称的图形△A2B2C2,则顶点A2的坐标是(B)
A.(-3,2) B.(2,-1) C.(1,-2) D.(3,-1)
12.(2018·邢台四校期中联考)平面直角坐标系中的四边形ABCD,各顶点的横、纵坐标均扩大为原来的2倍,四边形ABCD的形状不变(填“改变”或“不变”),面积变为原来的4倍.
13.如图,在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
①(4,5),(0,3),(1,3),(7,3),(8,3),(4,5);
②(1,3),(1,0),(7,0),(7,3).
(1)观察所得的图形,你觉得它像什么?
(2)求出这个图形的面积;
(3)怎样变换坐标,才能使得到的图形与(1)中的图形关于x轴对称.
解:如图所示.
(1)像一所“房子”.
(2)此图形的面积为×8×2+6×3=26.
(3)将各点的纵坐标乘-1,横坐标保持不变,所得的图形与(1)中的图形关于x轴对称.
14.在平面直角坐标系中画出一个以A(-1,-1),B(2,-1),C(2,2),D(-1,2)为顶点的图形,说明这是什么图形?把各顶点的坐标都乘2,得到的图形的面积与原图形面积有怎样的关系?你再做一做用不同的k(k>0)值去乘各顶点的坐标,发现随着k的变化,图形的面积是怎样变化的?
解:如图,画出以A,B,C,D为顶点的图形,这是一个正方形,它的边长为3.
把各顶点的坐标都乘2,得A′(-2,-2),B′(4,-2),C′(4,4),D′(-2,4),画出一个正方形,它的边长是6,所画正方形的面积是原正方形面积的4倍.
若把各顶点的坐标乘k(k>1),则所得图形面积为原图形面积的k2倍;若把各顶点的坐标乘k(0<k<1),则所得图形面积缩小为原图形面积的k2.
03 综合题
15.(2017·沧州期中)如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标是(16,3),B4的坐标是(32,0);
(2)若按(1)中的变换,将△OAB进行n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,推测An的坐标是(2n,3),Bn的坐标是(2n+1,0).
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
