高中数学第1章常用逻辑用语1.1.1四种命题课件6苏教版选修2_1(21ppt)
文档属性
| 名称 | 高中数学第1章常用逻辑用语1.1.1四种命题课件6苏教版选修2_1(21ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 241.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-04 00:00:00 | ||
图片预览








文档简介
课件21张PPT。命题及其关系(一)---四种命题问题1:下列语句的表述形式有什么特点?你能判断它们的真假吗?
①若xy=1,则x、y互为倒数;
②相似三角形的周长相等;
③2+4=5
④如果b≤-1,那么方程x2-2bx+b2+b=0有实根;
⑤垂直于同一条直线的两条直线平行吗?
其中是命题的是______________真命题为_________假命题为_________;
其中是命题的是①②③④
①④为真命题,②③为假命题;命题的定义 可以判断真假的陈述句,叫做命题;其中判断为真的命题,为真命题;判断为假的命题,为假命题;问题2:你能观察发现各命题之间有什么关系?①如果两个三角形全等,那么它们的面积相等;
②如果两个三角形的面积相等,那么它们全等;
③如果两个三角形不全等,那么它们的面积不相等;
④如果两个三角形不相等,那么它们不全等;三 【数学理论】----四种命题的概念命题(1)与(2)对比发现,交换原命题的条件和结论,所得的命题是逆命题
命题(1)与(3)对比发现,同时否定原命题的条件和结论,所得的命题是否命题
命题(1)与(4)对比发现,交换原命题的条件和结论,并且同时否定,所得的命题是逆否命题 三个
概念四 【四种命题的形式及其关系】一般的,我们用p和q分别表示原命题的条件和结论,用┐p和┐q分别表示p和q的否定,于是四种命题的形式就是:
原命题:若p则q;
逆命题:若q则p;
否命题:若┐p则┐q;
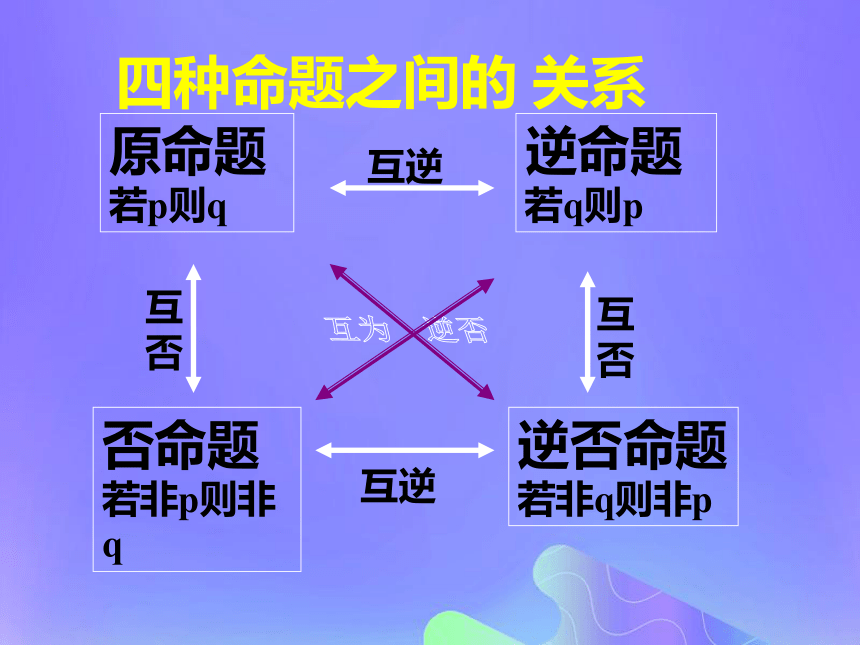
逆否命题:若┐q则┐p.我们已经知道命题①与命题②③④之间的关系,那么任意两个命题之间有什么关系?四种命题之间的 关系原命题
若p则q逆命题
若q则p否命题
若非p则非q逆否命题
若非q则非p互逆互否互否互逆互为 逆否【巩固运用】例1. 写出命题“若a=0,则ab=0”的逆命题、否命题、逆否命题,并判断各命题的真假。原命题:若a=0,则ab=0 真命题;
逆命题:若ab=0,则a=0 假命题;
否命题:若a 0,则ab 0 假命题;
逆否命题:若ab 0,则a 0 真命题;例2 把下列命题改写成“若p则q”的形式,并写出它们的逆命题,否命题与逆否命题,同时指出它们的真假: (1)对顶角相等;
(2)四条边相等的四边形是正方形.原命题:若两个角是对顶角,则这两个角相等 (真)
逆命题:若两个角相等,则这两个角是对顶角 (假)
否命题:若两个角不是对顶角,则这两个角不相等 (假)
逆否命题:若两个角不相等,则这两个角不是对顶角 (真)原命题:若一个四边形四边相等,则它是正方形;(假)
逆命题:若一个四边形是正方形,则它的四条边相等;(真)
否命题:若一个四边形四边不相等,则它不是正方形;(真)
逆否命题:若一个四边形不是正方形,则它的四条边不相等;(假)结论:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则Q”的形式)注意:三种命题中最难写 的是否命题。【思考】通过以上学习,你认为如果原命题为真,那么它的逆命题、否命题、逆否命题的真假性是怎样的?结论:因此四种命题的真假性之间的关系如下: (1)两个命题互为逆否命题,它们有相同的真假性; (2)两个命题为互逆命题或互否命题,它们的真假性没有关系.归纳延伸
①若xy=1,则x、y互为倒数;
②相似三角形的周长相等;
③2+4=5
④如果b≤-1,那么方程x2-2bx+b2+b=0有实根;
⑤垂直于同一条直线的两条直线平行吗?
其中是命题的是______________真命题为_________假命题为_________;
其中是命题的是①②③④
①④为真命题,②③为假命题;命题的定义 可以判断真假的陈述句,叫做命题;其中判断为真的命题,为真命题;判断为假的命题,为假命题;问题2:你能观察发现各命题之间有什么关系?①如果两个三角形全等,那么它们的面积相等;
②如果两个三角形的面积相等,那么它们全等;
③如果两个三角形不全等,那么它们的面积不相等;
④如果两个三角形不相等,那么它们不全等;三 【数学理论】----四种命题的概念命题(1)与(2)对比发现,交换原命题的条件和结论,所得的命题是逆命题
命题(1)与(3)对比发现,同时否定原命题的条件和结论,所得的命题是否命题
命题(1)与(4)对比发现,交换原命题的条件和结论,并且同时否定,所得的命题是逆否命题 三个
概念四 【四种命题的形式及其关系】一般的,我们用p和q分别表示原命题的条件和结论,用┐p和┐q分别表示p和q的否定,于是四种命题的形式就是:
原命题:若p则q;
逆命题:若q则p;
否命题:若┐p则┐q;
逆否命题:若┐q则┐p.我们已经知道命题①与命题②③④之间的关系,那么任意两个命题之间有什么关系?四种命题之间的 关系原命题
若p则q逆命题
若q则p否命题
若非p则非q逆否命题
若非q则非p互逆互否互否互逆互为 逆否【巩固运用】例1. 写出命题“若a=0,则ab=0”的逆命题、否命题、逆否命题,并判断各命题的真假。原命题:若a=0,则ab=0 真命题;
逆命题:若ab=0,则a=0 假命题;
否命题:若a 0,则ab 0 假命题;
逆否命题:若ab 0,则a 0 真命题;例2 把下列命题改写成“若p则q”的形式,并写出它们的逆命题,否命题与逆否命题,同时指出它们的真假: (1)对顶角相等;
(2)四条边相等的四边形是正方形.原命题:若两个角是对顶角,则这两个角相等 (真)
逆命题:若两个角相等,则这两个角是对顶角 (假)
否命题:若两个角不是对顶角,则这两个角不相等 (假)
逆否命题:若两个角不相等,则这两个角不是对顶角 (真)原命题:若一个四边形四边相等,则它是正方形;(假)
逆命题:若一个四边形是正方形,则它的四条边相等;(真)
否命题:若一个四边形四边不相等,则它不是正方形;(真)
逆否命题:若一个四边形不是正方形,则它的四条边不相等;(假)结论:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则Q”的形式)注意:三种命题中最难写 的是否命题。【思考】通过以上学习,你认为如果原命题为真,那么它的逆命题、否命题、逆否命题的真假性是怎样的?结论:因此四种命题的真假性之间的关系如下: (1)两个命题互为逆否命题,它们有相同的真假性; (2)两个命题为互逆命题或互否命题,它们的真假性没有关系.归纳延伸
