2.1两条直线的位置关系（1）课件

课件24张PPT。第二章 相交线与平行线2.1 两直线的位置关系2.1.1 相交线观察这些图片，你能否看到相交线、平行线？情景导入1.在生活中，你常见的同一平面内的两直线有哪些位置关系？
你能给它们下定义吗？
提示：同一平面内的两直线有两种位置关系：
_____和_____.
相交线：在同一平面内，若两条直线_________公共点，我们称
这两条直线为相交线.
平行线：在同一平面内，_______的两条直线叫做平行线.只有一个不相交相交平行探究一2.阅读相关内容，归纳对顶角的概念与性质.
定义：有_____顶点,且两边互为反向延长线的两个角叫做________.
性质：对顶角_____.公共对顶角相等∠1与∠3有怎样的位置关系？思考对顶角探究二图中还有哪些对顶角？对顶角的定义：∠1和∠3有一个公共顶点O，并且∠1的两边分别是∠3的两边的反向延长线，具有这种位置关系的两个角，互为对顶角.归纳【规律总结】理解对顶角需要注意的三点
1.对顶角是成对出现的，不能单独说一个角是对顶角.
2.对顶角反映两角相等的数量关系.
3.对顶角还反映两角的位置关系.利用对顶角定义寻找对顶角必须具备的两个要素是什么？
提示：(1)有公共顶点.(2)两边互为反向延长线.归纳余角和补角的概念与性质.
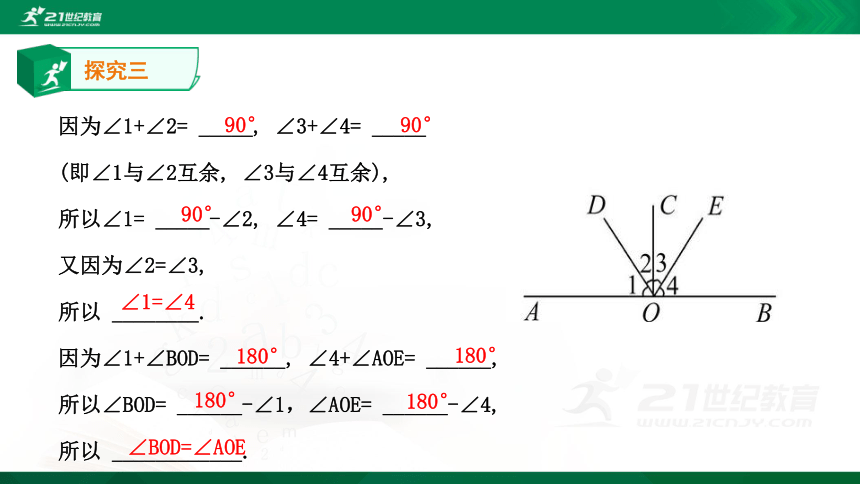
已知：如图,∠AOC=∠BOC=90°,∠2=∠3,试说明∠1与∠4, ∠AOE 与∠BOD的关系.探究三因为∠1+∠2= _____, ∠3+∠4= _____
(即∠1与∠2互余, ∠3与∠4互余),
所以∠1= _____-∠2, ∠4= _____-∠3,
又因为∠2=∠3,
所以 ________.
因为∠1+∠BOD= ______, ∠4+∠AOE= ______,
所以∠BOD= ______-∠1，∠AOE= ______-∠4,
所以 ____________.90°90°90°90°∠1=∠4180°180°180°180°∠BOD=∠AOE1.概念：(1)如果两个角的和是_____,那么称这两个角互为余角.
(2)如果两个角的和是______,那么称这两个角互为补角.
2.性质：同角或等角的余角_____,同角或等角的补角_____.90°180°相等相等归纳1.任何角都有余角吗？
提示：由余角的定义可知，只有小于直角的角才有余角.
2.“相等的角是对顶角”这句话对吗？
提示：不对，对顶角是与两角的位置有关系的，必须是有公共顶点,且两边互为反向延长线的两个角叫对顶角.延伸拓展理解余角与补角需要注意的四点
1.余角与补角是针对两个角而言，并且是相互的.
2.互为余角、互为补角的两个角，只与它们的大小有关，与它们的位置无关.
3.同一个角的补角比它的余角大90°.
4.互余的两个角必须是两个锐角，而互补的两个角可以是一个锐角和一个钝角，也可以是两个直角. 余角与补角
【例】已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.
【解题探究】(1)设这个角为x°,则它的余角与补角应怎样表示？
答：它的余角为(90-x)°,补角为(180-x)°.巩固提高(2)题目中的相等关系是什么？
答：一个角的补角=这个角的余角的3倍+10°.
(3)根据题意,得180-x=3(90-x)+10，
解得x=50.
答：这个角的度数为50°.1.下列说法中，正确的有（　 ）①对顶角相等②相等的角是对顶角③不是对顶角的两个角就不相等④不相等的角不是对顶角A．1个 B．2个 C．3个 D．0个B√√随堂练习2.图中给出的各角，哪些互为补角？10o30o60o80o100o120o150o170o3.图中给出的各角，哪些互为余角？15o24o66o75o46.2o43.8o4.如图已知：直线AB与CD交于点O, ∠EOD=900,
回答下列问题：
（1）∠AOE的余角是 ；补角是 ；
（2）∠AOC的余角是 ；补角是 ；
对顶角是 ； ∠AOC∠BOE∠AOE∠BOC∠BOD1.若一个角的补角等于它的余角的4 倍，求这个角的度数.解：设这个角是x°，则它的补角是(180°－x°), 余角是(90°－x°) .
根据题意，得180°－x°= 4 (90°－x°).
解得 x=60.
答：这个角的度数是60 °.拓展提高2.要测量两堵墙所成的角的度数，但人不能进入
围墙，如何测量？O你能想到几种方法？相交线补角对顶角互 补相 等余角5互 余课堂总结作业布置习题2.1 P40
第一题，第三题谢谢21世纪教育网（www.21cnjy.com) 中小学教育资源网站 有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php