华东师大版八年级下册17.5实践与探索同步测试卷(附答案)
文档属性
| 名称 | 华东师大版八年级下册17.5实践与探索同步测试卷(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 167.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-05 08:40:09 | ||
图片预览




文档简介
函数及其图象(17.5)同步测试
一、选择(每小题3分,共24分)
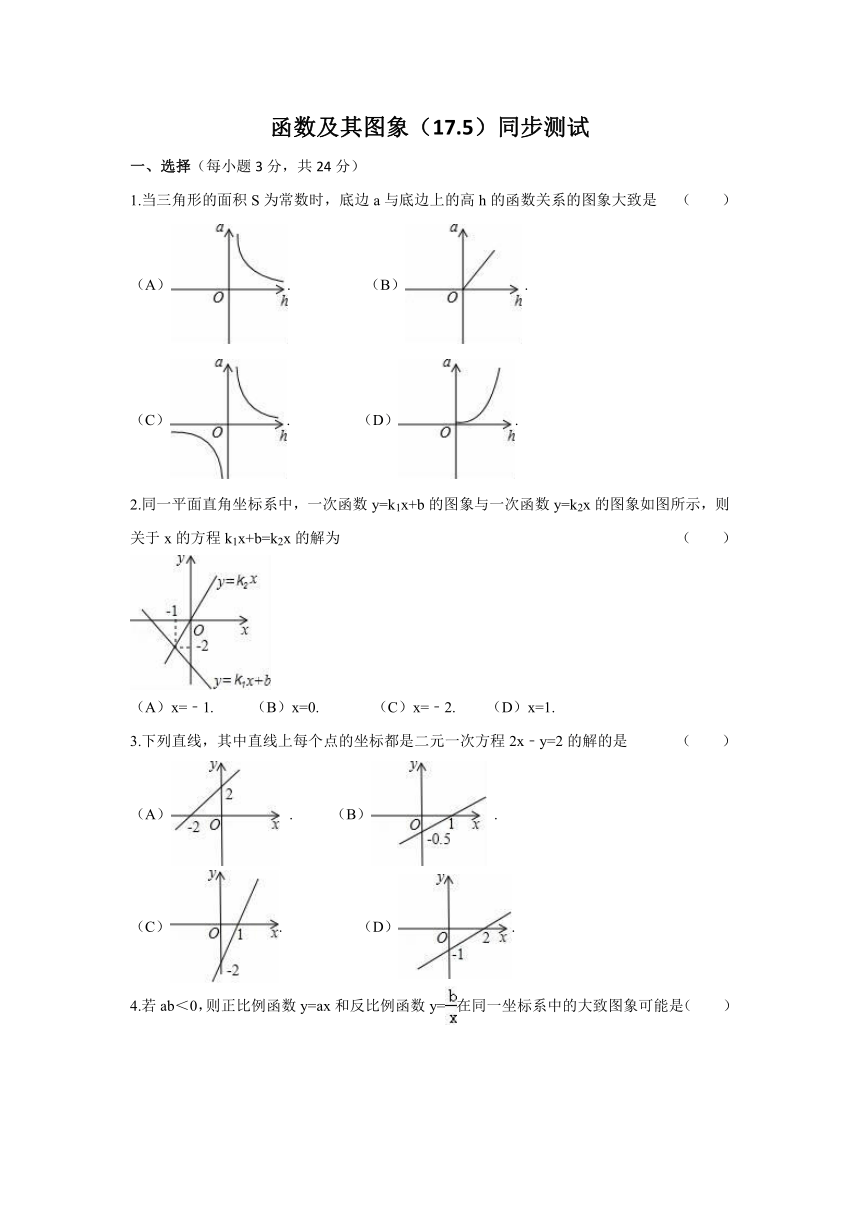
1.当三角形的面积S为常数时,底边a与底边上的高h的函数关系的图象大致是 ( )
(A). (B) .
(C). (D).
2.同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为 ( )
(A)x=﹣1. (B)x=0. (C)x=﹣2. (D)x=1.
3.下列直线,其中直线上每个点的坐标都是二元一次方程2x﹣y=2的解的是 ( )
(A) . (B) .
(C). (D).
4.若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图象可能是( )
(A). (B). (C). (D).
5.如图,已知直线y1=x+a与y2=kx+b相交于点P(﹣1,2),则关于x的不等式x+a>kx+b的解集正确的是 ( )
(A)x>1. (B)x>﹣1. (C)x<1. (D)x<﹣1.
6.已知三条直线L1:(m﹣2)x﹣y=1、L2:x﹣y=3、L3:2x﹣y=2相交于同一点,则m=( )
(A)6. (B)5. (C)4. (D)﹣3.
7.如图是某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则下列结论中正确的共有 ( )
(1)若通话时间少于120分,则A方案比B方案便宜
(2)若通话时间超过200分,则B方案比A方案便宜
(3)若通讯费用为60元,则B方案比A方案的通话时间多
(4)当通话时间为170分钟时,A方案与B方案的费用相等
(A)1个. (B)2个. (C)3个. (D)4个.
8.图,一次函数y=kx﹣1的图象与x轴交于点A,与反比例函数y=(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是 ( )
(A)1. (B)2. (C)3. (D)4.
二、填空(每小题4分,共32分)
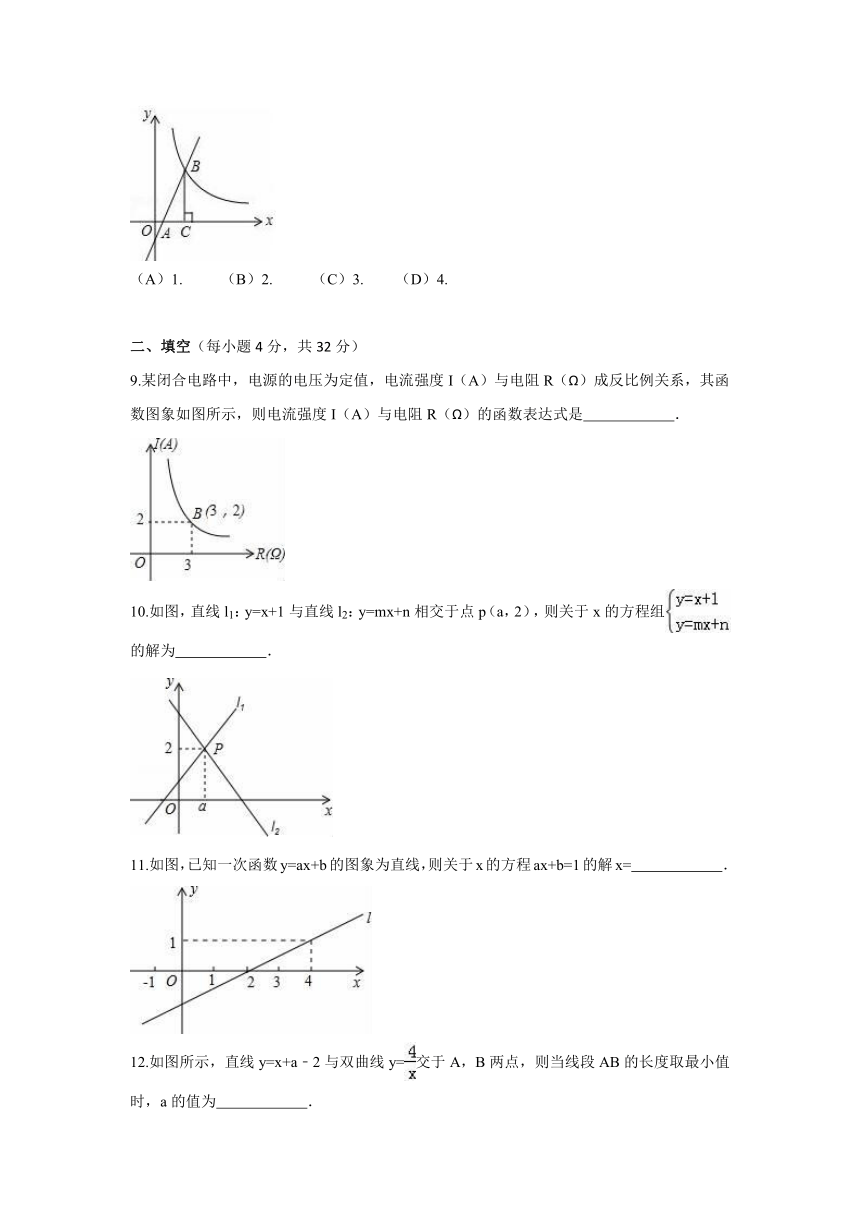
9.某闭合电路中,电源的电压为定值,电流强度I(A)与电阻R(Ω)成反比例关系,其函数图象如图所示,则电流强度I(A)与电阻R(Ω)的函数表达式是 .
10.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点p(a,2),则关于x的方程组的解为 .
11.如图,已知一次函数y=ax+b的图象为直线,则关于x的方程ax+b=1的解x= .
12.如图所示,直线y=x+a﹣2与双曲线y=交于A,B两点,则当线段AB的长度取最小值时,a的值为 .
13.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,则旅客可携带的免费行李的最大质量为 kg.
14.如图,正比例函数y=2x与一次函数y=kx+4的图象交于点A(m,2),则不等式2x<kx+4的解集为 .
15.已知反比例函数y=的图象与一次函数y=x﹣2的图象相交于点P(a,b),则﹣= .
16.直线y=2x+m和直线y=3x+3的交点在第二象限,则m的取值范围 .
三、解答(4个小题,共44分)
17.(10分)已知直线y=3x与直线y=﹣2x+b交点为(2,m),试确定方程组的解和m,b的值.
18.(10分)为了鼓励小强做家务,小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成.若设小强每月的家务劳动时间为x小时.下月他可获得的生活总费用为y元,則y(元)和x(小时)之间的函数图象如图所示.
(1)根据图象回答问题:小强每月的基本生活费是 ;若小强4月份做家务10小时,則他5月份能获得 元生活总费用;
(2)根据图象求出AB段的函数表达式;
(3)若小強希望5月份有250元的生活总费用,则小强4月份需做家务多少小时?
19.(12分)2018年入春以来,北方部分地区干旱严重,导致凤凰社区人畜饮用水紧张.每天需从社区外调运饮用水120吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点.甲厂每天最多可调出80吨.乙厂每天最多可调出90吨.从两水厂运水到凤凰社区供水点的路程和运费如下表:
到凤凰社区供水点的路程(千米)
运费(元/吨?千米)
甲厂
20
12
乙厂
14
15
(1)设从甲厂调运饮用水x吨.总运费为w元.试写出w与x的函数关系式.
(2)怎样安排调运方案才能使每天的总运费最省?
20.(12分)如图,直线y=mx与双曲线y=相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
(1)求反比例函数的表达式;
(2)求△ABC的面积;
(3)根据图象直接写出当mx>时,x的取值范围.
附加题(2个小题,共20分)
1.(10分)如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
(2)根据该食品制作要求,在材料温度不低于12℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
2.(10分)我们知道,图形通过平移、旋转、翻折变换后,不改变图形的形状和大小,只改变图形的位置.
(1)一次函数y=x﹣1的图象是由正比例函数y=x图象向 平移 个单位长度得到;
(2)已知函数y=(x>0)图象如图①,在同一坐标系中画出函数y=(x>﹣1)的图象,并观察函数y=的图象是由函数y=图象经过怎样的变换得到的;
(3)在平面直角坐标系中,矩形ABCD位置如图②,其中A、B、C三点的坐标分别为A(1,﹣1)、B(1,﹣2)、C(4,﹣2),现将反比例函数y=图象沿x轴正方向平移,若平移速度为每秒1个单位长度.
①设函数图象平移时间为t秒,求函数图象与矩形ABCD有公共点时t的取值范围;
②在平移过程中,当函数图象与矩形ABCD有公共点时,求函数图象扫过的区域夹在直线AD、BC之间的图形面积.
参考答案
一、1.A 2.A 3.C 4.C 5.B 6.B 7.D 8.B
二、9. I= 10. 11.4 12.2 13.20 14.x<1 15.﹣2 16.2<m<3
三、17. 解:∵直线y=3x与直线y=﹣2x+b交点为(2,m),
∴,解得,
∴方程组的解为.
∴方程组的解为,m、b的值分别是6、10.
18.解:(1)观察图象可得:小强每月的基本生活费是150元,若小强4月份做家务10小时,則他5月份能获得175元生活总费用;
故答案为:150元、175.
(2)设AB段的函数表达式:y=kx+b,将A(0,150)、B(20,200)代入,得:
,解得:
∴AB段的函数关系式是:y=2.5x+150;
(3)设BC段的函数关系式:y=kx+b,则
,解得:
∴BC段的函数关系式:y=4x+120,
把y=250代入,得:x=32.5
答:小强4月份需做家务32.5小时.
19.解:(1)w=20×12x+14×15(120﹣x),
即w=30x+25200;
(2)根据题意得:,
解得:30≤x≤80.
当x=30时w取得最小值.
则120﹣30=90(吨),
答:当从甲调30吨,从乙调90吨,总运费最省.
20.解:(1)把A(1,2)代入y=mx得m=2,则表达式是y=2x,
把A(1,2)代入y=得:k=2,
则反比例函数表达式是y=;
(2)A的坐标是(1,2),则B的坐标是(﹣1,﹣2).
∴当以AC为底边时,△ABC的高为2+2=4,
∴S△ABC=×2×4=4;
(3)根据图象可得:﹣1<x<0或x>1.
附加题:
1. 解:(1)设加热停止后反比例函数表达式为y=,
∵y=过(12,14),得k1=12×14=168,
则y=;
当y=28时,28=,得x=6.
设加热过程中一次函数表达式y=k2x+b,
由图象知y=k2x+b过点(0,4)与(6,28),
∴,解得,
∴y=4x+4,此时x的范围是0≤x≤6.
y=此时x的范围是x>6;
(2)当y=12时,由y=4x+4,
得x=2.
由y=,
得x=14,
所以对该材料进行特殊处理所用的时间为14﹣2=12(分钟).
2.解:(1)一次函数y=x﹣1的图象是由正比例函数y=x图象向下平移1个单位长度得到,故答案为:下,1;
(2)如图1:
,
函数y=的图象是由函数y=图象经向左平移一个单位得到的.
(3)①当函数y=的图象经过点B时,函数表达式为y=,
当函数y=的图象经过点D时,函数表达式为y=,
由函数图象平移规律得2≤t≤6;
②如图2,函数图象扫过的区域夹在直线AD、BC之间的图形是图形AEBFD
图形ABE向右平移3个单位,得图形DGF,
图形DGF与图形CDF组合成边长为1的正方形CFGD,
S=3×1+1×1=4.
一、选择(每小题3分,共24分)
1.当三角形的面积S为常数时,底边a与底边上的高h的函数关系的图象大致是 ( )
(A). (B) .
(C). (D).
2.同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为 ( )
(A)x=﹣1. (B)x=0. (C)x=﹣2. (D)x=1.
3.下列直线,其中直线上每个点的坐标都是二元一次方程2x﹣y=2的解的是 ( )
(A) . (B) .
(C). (D).
4.若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图象可能是( )
(A). (B). (C). (D).
5.如图,已知直线y1=x+a与y2=kx+b相交于点P(﹣1,2),则关于x的不等式x+a>kx+b的解集正确的是 ( )
(A)x>1. (B)x>﹣1. (C)x<1. (D)x<﹣1.
6.已知三条直线L1:(m﹣2)x﹣y=1、L2:x﹣y=3、L3:2x﹣y=2相交于同一点,则m=( )
(A)6. (B)5. (C)4. (D)﹣3.
7.如图是某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则下列结论中正确的共有 ( )
(1)若通话时间少于120分,则A方案比B方案便宜
(2)若通话时间超过200分,则B方案比A方案便宜
(3)若通讯费用为60元,则B方案比A方案的通话时间多
(4)当通话时间为170分钟时,A方案与B方案的费用相等
(A)1个. (B)2个. (C)3个. (D)4个.
8.图,一次函数y=kx﹣1的图象与x轴交于点A,与反比例函数y=(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是 ( )
(A)1. (B)2. (C)3. (D)4.
二、填空(每小题4分,共32分)
9.某闭合电路中,电源的电压为定值,电流强度I(A)与电阻R(Ω)成反比例关系,其函数图象如图所示,则电流强度I(A)与电阻R(Ω)的函数表达式是 .
10.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点p(a,2),则关于x的方程组的解为 .
11.如图,已知一次函数y=ax+b的图象为直线,则关于x的方程ax+b=1的解x= .
12.如图所示,直线y=x+a﹣2与双曲线y=交于A,B两点,则当线段AB的长度取最小值时,a的值为 .
13.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,则旅客可携带的免费行李的最大质量为 kg.
14.如图,正比例函数y=2x与一次函数y=kx+4的图象交于点A(m,2),则不等式2x<kx+4的解集为 .
15.已知反比例函数y=的图象与一次函数y=x﹣2的图象相交于点P(a,b),则﹣= .
16.直线y=2x+m和直线y=3x+3的交点在第二象限,则m的取值范围 .
三、解答(4个小题,共44分)
17.(10分)已知直线y=3x与直线y=﹣2x+b交点为(2,m),试确定方程组的解和m,b的值.
18.(10分)为了鼓励小强做家务,小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成.若设小强每月的家务劳动时间为x小时.下月他可获得的生活总费用为y元,則y(元)和x(小时)之间的函数图象如图所示.
(1)根据图象回答问题:小强每月的基本生活费是 ;若小强4月份做家务10小时,則他5月份能获得 元生活总费用;
(2)根据图象求出AB段的函数表达式;
(3)若小強希望5月份有250元的生活总费用,则小强4月份需做家务多少小时?
19.(12分)2018年入春以来,北方部分地区干旱严重,导致凤凰社区人畜饮用水紧张.每天需从社区外调运饮用水120吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点.甲厂每天最多可调出80吨.乙厂每天最多可调出90吨.从两水厂运水到凤凰社区供水点的路程和运费如下表:
到凤凰社区供水点的路程(千米)
运费(元/吨?千米)
甲厂
20
12
乙厂
14
15
(1)设从甲厂调运饮用水x吨.总运费为w元.试写出w与x的函数关系式.
(2)怎样安排调运方案才能使每天的总运费最省?
20.(12分)如图,直线y=mx与双曲线y=相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
(1)求反比例函数的表达式;
(2)求△ABC的面积;
(3)根据图象直接写出当mx>时,x的取值范围.
附加题(2个小题,共20分)
1.(10分)如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
(2)根据该食品制作要求,在材料温度不低于12℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
2.(10分)我们知道,图形通过平移、旋转、翻折变换后,不改变图形的形状和大小,只改变图形的位置.
(1)一次函数y=x﹣1的图象是由正比例函数y=x图象向 平移 个单位长度得到;
(2)已知函数y=(x>0)图象如图①,在同一坐标系中画出函数y=(x>﹣1)的图象,并观察函数y=的图象是由函数y=图象经过怎样的变换得到的;
(3)在平面直角坐标系中,矩形ABCD位置如图②,其中A、B、C三点的坐标分别为A(1,﹣1)、B(1,﹣2)、C(4,﹣2),现将反比例函数y=图象沿x轴正方向平移,若平移速度为每秒1个单位长度.
①设函数图象平移时间为t秒,求函数图象与矩形ABCD有公共点时t的取值范围;
②在平移过程中,当函数图象与矩形ABCD有公共点时,求函数图象扫过的区域夹在直线AD、BC之间的图形面积.
参考答案
一、1.A 2.A 3.C 4.C 5.B 6.B 7.D 8.B
二、9. I= 10. 11.4 12.2 13.20 14.x<1 15.﹣2 16.2<m<3
三、17. 解:∵直线y=3x与直线y=﹣2x+b交点为(2,m),
∴,解得,
∴方程组的解为.
∴方程组的解为,m、b的值分别是6、10.
18.解:(1)观察图象可得:小强每月的基本生活费是150元,若小强4月份做家务10小时,則他5月份能获得175元生活总费用;
故答案为:150元、175.
(2)设AB段的函数表达式:y=kx+b,将A(0,150)、B(20,200)代入,得:
,解得:
∴AB段的函数关系式是:y=2.5x+150;
(3)设BC段的函数关系式:y=kx+b,则
,解得:
∴BC段的函数关系式:y=4x+120,
把y=250代入,得:x=32.5
答:小强4月份需做家务32.5小时.
19.解:(1)w=20×12x+14×15(120﹣x),
即w=30x+25200;
(2)根据题意得:,
解得:30≤x≤80.
当x=30时w取得最小值.
则120﹣30=90(吨),
答:当从甲调30吨,从乙调90吨,总运费最省.
20.解:(1)把A(1,2)代入y=mx得m=2,则表达式是y=2x,
把A(1,2)代入y=得:k=2,
则反比例函数表达式是y=;
(2)A的坐标是(1,2),则B的坐标是(﹣1,﹣2).
∴当以AC为底边时,△ABC的高为2+2=4,
∴S△ABC=×2×4=4;
(3)根据图象可得:﹣1<x<0或x>1.
附加题:
1. 解:(1)设加热停止后反比例函数表达式为y=,
∵y=过(12,14),得k1=12×14=168,
则y=;
当y=28时,28=,得x=6.
设加热过程中一次函数表达式y=k2x+b,
由图象知y=k2x+b过点(0,4)与(6,28),
∴,解得,
∴y=4x+4,此时x的范围是0≤x≤6.
y=此时x的范围是x>6;
(2)当y=12时,由y=4x+4,
得x=2.
由y=,
得x=14,
所以对该材料进行特殊处理所用的时间为14﹣2=12(分钟).
2.解:(1)一次函数y=x﹣1的图象是由正比例函数y=x图象向下平移1个单位长度得到,故答案为:下,1;
(2)如图1:
,
函数y=的图象是由函数y=图象经向左平移一个单位得到的.
(3)①当函数y=的图象经过点B时,函数表达式为y=,
当函数y=的图象经过点D时,函数表达式为y=,
由函数图象平移规律得2≤t≤6;
②如图2,函数图象扫过的区域夹在直线AD、BC之间的图形是图形AEBFD
图形ABE向右平移3个单位,得图形DGF,
图形DGF与图形CDF组合成边长为1的正方形CFGD,
S=3×1+1×1=4.
